Integrale de Fresnel

Integrale de Fresnel: Intégrale de Fresnel

Pour les articles homonymes, voir Fresnel.

L'intégrale de Fresnel est une intégrale impropre introduite par le physicien français Augustin Fresnel.

Formule de Fresnel
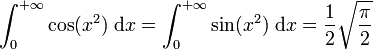
$\int_{0}^{+\infty} \cos(x^2)\;\mathrm{d}x = \int_{0}^{+\infty} \sin(x^2)\;\mathrm{d}x = \frac{1}{2}\sqrt{\frac{\pi}{2}}$
On en déduit l'intégrale de Fresnel complexe :
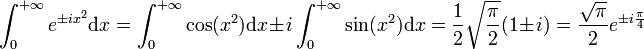
$\int_{0}^{+\infty} e^{\pm i x^2} \mathrm{d}x = \int_{0}^{+\infty} \cos(x^2)\mathrm{d}x \pm i \int_{0}^{+\infty} \sin(x^2)\mathrm{d}x = \frac{1}{2}\sqrt{\frac{\pi}{2}}( 1 \pm i ) = \frac{\sqrt{\pi}}{2} e^{\pm i\frac{\pi}{4}}$
Calcul de l'intégrale de Fresnel

Considérons pour tout réel $t$ la fonction de ℝ⁺ dans ℂ définie par
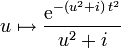$u\mapsto {\mathrm{e}^{-(u^2+i)\,t^2}\over u^2+i}$ .
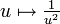Cette fonction est intégrable puisqu'étant continue sur ℝ⁺ et, avec $Re( - (u 2 + i)) < 0$ , négligeable au voisinage de +∞ devant $u\mapsto\displaystyle\tfrac{1}{u^2}$ .

Il est donc possible de poser $f$ , la fonction définie pour tout $t$ par l'intégrale à paramètre suivante :
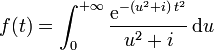
$f(t)=\int_0^{+\infty}\frac{\mathrm{e}^{-(u^2+i)\,t^2}}{u^2+i}\,\mathrm{d}u$
On montre que f est de classe $C 1$ sur $ℝ +*$ et que

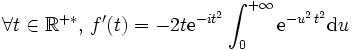$\forall t\in\R^{+*},\,f'(t)=-2t\mathrm{e}^{-it^2}\int_{0}^{+\infty}\mathrm{e}^{-u^2\,t^2}\mathrm{d}u$

Démonstration

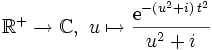
Pour tout $t > 0$ , la fonction $\R^+\rightarrow\mathbb C,\ u\mapsto {\mathrm{e}^{-(u^2+i)\,t^2}\over u^2+i}$ est continue par morceaux et intégrable.

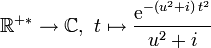
Pour tout {{u ∈ ℝ⁺}}, la fonction $\R^{+*}\rightarrow\mathbb C,\ t\mapsto {\mathrm{e}^{-(u^2+i)\,t^2}\over u^2+i}$ est dérivable et de dérivée $f'(t) = - 2 t exp( - (u 2 + i) t 2)$

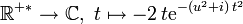
Pour tout {{u ∈ ℝ⁺}}, la fonction $\R^{+*}\rightarrow\mathbb C,\ t\mapsto {-2\,t}\mathrm{e}^{-(u^2+i)\,t^2}$ est continue par morceaux et intégrable

Pour tout {{t ∈ ℝ^+*}}, la fonction $\R^{+*}\rightarrow\mathbb C,\ u\mapsto {-2\,t}\exp {[-(u^2+i)\,t^2]}$ est continue

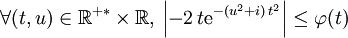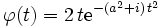Condition de domination : confinons le paramètre $u$ au compact {{[a,b] ⊂ ℝ^+*}} (donc $a > 0$ ). Exhibons $\varphi$ , une fonction continue par morceaux et intégrable sur ℝ⁺ vérifiant $\forall (t,u)\in\R^{+*}\times\R,\,\left|{-2\,t}\mathrm{e}^{-(u^2+i)\,t^2}\right|\le \varphi(t)$ . $\varphi(t)= 2\,t\mathrm{e}^{-(a^2+i)\,t^2}$ convient.

Conclusion : f est de classe $C 1$ sur {{math|ℝ^+*}} et
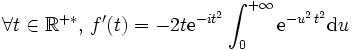
$\forall t\in\R^{+*},\,f'(t)=-2t\mathrm{e}^{-it^2}\int_{0}^{+\infty}\mathrm{e}^{-u^2\,t^2}\mathrm{d}u$

En opérant un changement de variable linéaire par la fonction $ℝ + \to ℝ +, u \mapsto u\cdott = v$ , on aboutit immédiatement à, pour tout $t \in ℝ +*$ :
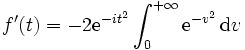
$f'(t)=-2\mathrm{e}^{-it^2}\int_{0}^{+\infty}\mathrm{e}^{-v^2}\,\mathrm{d}v$
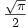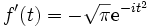L'intégrale définie est ici bien connue (voir l'article sur l'intégrale de Gauss) et vaut $\tfrac{\sqrt{\pi}}{2}$ . Ainsi, on a une expression plus simple de la dérivée de $f$ : $f'(t)=-\sqrt{\pi}\mathrm{e}^{-it^2}$ .

L'application du théorème de convergence dominée permet de montrer que 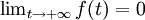$\textstyle\lim_{t\to+\infty}f(t)=0$ Considérons la suite de fonctions $(f n)$ définie par :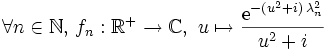
$\forall n\in\N,\,f_n:\R^+\rightarrow\mathbb C,\ u\mapsto {\mathrm{e}^{-(u^2+i)\,\lambda_n^2}\over u^2+i}$
où $(λ n)$ est une suite réelle croissante de limite +∞. Montrons que
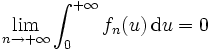
$\lim_{n\rightarrow +\infty}\int_{0}^{+\infty}f_n(u)\,\mathrm{d}u=0$
c'est-à-dire que, d'après la caractérisation séquentielle des limites :
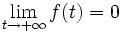$\lim_{t\rightarrow +\infty}f(t)=0$ .
Nous savons d'ores et déjà que $(f n)$ converge simplement vers
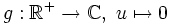$g:\R^+\rightarrow\mathbb C,\ u\mapsto 0$ .
Par conséquent, de l'expression de $f'$ , on déduit en intégrant sur ℝ⁺ (fonctions intégrables) :
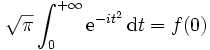
$\sqrt{\pi}\int_{0}^{+\infty}\mathrm{e}^{-it^2}\,\mathrm{d}t = f(0)$
D'autre part,
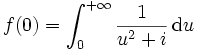$f(0)=\int_0^{+\infty}{1\over u^2+i}\,\mathrm{d}u$ .
On se sert alors d'une intégrale classique :
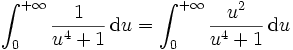
$\int_0^{+\infty}{1\over u^4+1}\,\mathrm{d}u=\int_0^{+\infty}{u^2\over u^4+1}\,\mathrm{d}u$
et de l'expression 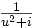$\tfrac1{u^2+i}$ sous la forme 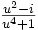$\tfrac{u^2-i}{u^4+1}$ pour en déduire que
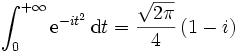$\int_{0}^{+\infty}\mathrm{e}^{-it^2}\,\mathrm{d}t = {\sqrt{2\pi}\over 4}\,(1-i)$ .
Il reste à prendre la partie réelle (respectivement la partie imaginaire) pour conclure que :
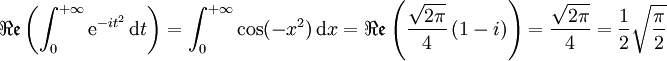
$\Re \mathfrak{e}\left(\int_{0}^{+\infty}\mathrm{e}^{-it^2}\,\mathrm{d}t\right) = \int_{0}^{+\infty}\cos(-x^2)\,\mathrm{d}x=\Re \mathfrak{e}\left({\sqrt{2\pi}\over 4}\,(1-i) \right)= {\sqrt{2\pi}\over 4} = \frac{1}{2}\sqrt{\frac{\pi}{2}}$
(respectivement que
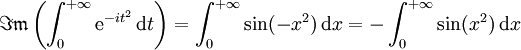
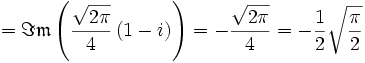
$\Im \mathfrak{m}\left(\int_{0}^{+\infty}\mathrm{e}^{-it^2}\,\mathrm{d}t\right) = \int_{0}^{+\infty}\sin(-x^2)\,\mathrm{d}x=-\int_{0}^{+\infty}\sin(x^2)\,\mathrm{d}x$ $=\Im \mathfrak{m}\left({\sqrt{2\pi}\over 4}\,(1-i) \right)= -{\sqrt{2\pi}\over 4} = -\frac{1}{2}\sqrt{\frac{\pi}{2}}$
).

Autre calcul possible

Il est aussi possible d'intégrer $f (z) = exp( - z 2)$ sur les bornes du triangle $T R$ de sommets 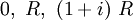$0, ~R, ~(1+i)~ R$ puis de faire tendre R vers l'infini.

Ce document provient de « Int%C3%A9grale de Fresnel ».

Catégorie : Intégrale

Contenu soumis à la licence CC-BY-SA. Source : Article Integrale de Fresnel de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Intégrale De Fresnel — Pour les articles homonymes, voir Fresnel. L intégrale de Fresnel est une intégrale impropre introduite par le physicien français Augustin Fresnel. Formule de Fresnel … Wikipédia en Français
Intégrale de fresnel — Pour les articles homonymes, voir Fresnel. L intégrale de Fresnel est une intégrale impropre introduite par le physicien français Augustin Fresnel. Formule de Fresnel … Wikipédia en Français
Intégrale de Fresnel — Pour les articles homonymes, voir Fresnel. L intégrale de Fresnel est une intégrale impropre introduite par le physicien français Augustin Fresnel. Sommaire 1 Formule de Fresnel 2 Définition … Wikipédia en Français
Fresnel — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Patronyme 2 Optique 3 M … Wikipédia en Français
Fresnel-Integral — Als Fresnel Integrale werden in der Mathematik die beiden uneigentlichen Integrale bezeichnet; sie ergeben sich aus dem gaußschen Fehlerintegral unter Benutzung des cauchyschen Integralsatzes. Fresnel kannte sie um 1819. Euler kannte schon 1781… … Deutsch Wikipedia
Intégrale définie — Table d intégrales Intégrales définies On appelle intégrale définie dans l intervalle [a,b] lorsque est une primitive quelconque de et que et … Wikipédia en Français
Comparaison Série-intégrale — Les séries sont un procédé de sommation de grandeurs discrètes, l intégrale de grandeurs continues. L analogie formelle entre les deux domaines permet de faire passer des idées intéressantes de l une à l autre. La comparaison explicite d une… … Wikipédia en Français
Comparaison serie-integrale — Comparaison série intégrale Les séries sont un procédé de sommation de grandeurs discrètes, l intégrale de grandeurs continues. L analogie formelle entre les deux domaines permet de faire passer des idées intéressantes de l une à l autre. La… … Wikipédia en Français
Comparaison série-intégrale — Les séries sont un procédé de sommation de grandeurs discrètes, l intégrale de grandeurs continues. L analogie formelle entre les deux domaines permet de faire passer des idées intéressantes de l une à l autre. La comparaison explicite d une… … Wikipédia en Français
Spirale de Fresnel — Clothoïde Pour les articles homonymes, voir Fresnel. Clothoïde La clothoïde est une courbe transcendante plane dont la courbure est proportionnelle à l abscisse curviligne … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Integrale de Fresnel

Intégrale de Fresnel

Formule de Fresnel

Calcul de l'intégrale de Fresnel

Autre calcul possible

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Integrale de Fresnel

Intégrale de Fresnel

Formule de Fresnel

Calcul de l'intégrale de Fresnel

Autre calcul possible

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link