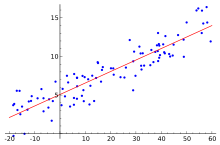
Régression linéaire

Pour les articles homonymes, voir Régression.

En statistiques, la régression linéaire désigne une approche pour modéliser la relation entre une variable aléatoire y et un vecteur de variables aléatoires x. De manière générale, le modèle linéaire peut s'écrire de la manière suivante :

$y = \beta_0 + \beta_1 x_1 + \ldots + \beta_K x_K + u$

y désigne la variable expliquée. Le vecteur x désigne l'ensemble des variables explicatives : $(x_1,x_2,\ldots,x_K)$ . u désigne le terme d'erreur. Il est parfois appelé perturbation.

On suppose qu'on dispose de données sur les variables $y, x_1, x_2, \ldots, x_K$ . On cherche à estimer le vecteur $β$ des paramètres : $(\beta_0,\beta_1, \ldots , \beta_K)$ . La régression est dite linéaire parce qu'elle impose une forme fonctionnelle linéaire dans les paramètres du modèle.

On parle aussi de modèle linéaire ou de modèle de régression linéaire.

En général, le modèle de régression linéaire désigne un modèle dans lequel l'espérance conditionnelle de y sachant x est une transformation affine de x. Cependant, on peut aussi considérer des modèles dans lesquels c'est la médiane conditionnelle de y sachant x ou n'importe quel quantile de la distribution de y sachant x qui est une transformation affine de x.

Le modèle de régression linéaire est souvent estimé par la méthode des moindres carrés mais il existe aussi de nombreuses autres méthodes pour estimer ce modèle. On peut par exemple estimer le modèle par maximum de vraisemblance ou encore par inférence bayésienne.

Bien qu'ils soient souvent présentés ensemble le modèle linéaire et la méthode des moindres carrés ne désignent pas la même chose. Le modèle linéaire désigne une classe de modèles qui peuvent être estimés par un grand nombre de méthodes et la méthode des moindres carrés désigne une méthode d'estimation. Elle peut être utilisée pour estimer différents types de modèles.

Sommaire

1 Histoire
2 Applications
3 Le modèle
4 Extensions
5 Références
6 Bibliographie
- 6.1 Manuels
7 Voir aussi
- 7.1 Articles connexes
- 7.2 Liens externes

Histoire

La première régression linéaire est attribuée à Francis Galton en 1886. Dans son article, Galton régresse la taille des fils en fonction de la taille des pères. Il constate un phénomène de régression vers la moyenne^[1].

Applications

Le modèle de régression linéaire a de nombreuses applications pratiques. Il permet notamment de faire des analyses de prédiction. Après avoir estimé un modèle de régression linéaire, on peut prédire quel serait le niveau de y pour des valeurs particulières de x.

Il permet également d'estimer l'effet d'une variable sur une autre en contrôlant par d'autres facteurs. Par exemple, dans le domaine des sciences de l'éducation, on peut évaluer l'effet de la taille des classes sur les performances scolaires des enfants en contrôlant par la catégorie socio-professionnelle des parents ou par l'emplacement géographique de l'établissement.

En économétrie

Le modèle linéaire est très utilisé en économétrie. Il est présenté dans de très nombreux manuels d'économie^[2].

En sciences politiques

En sociologie

Le modèle

Notations

On rencontre principalement trois types de notations.

La notation simple

$y_i = \beta_0 + \beta_1 x_{1,i} + \ldots + \beta_K x_{K,i} + u_{i}$

La notation vectorielle

Si on appelle $β$ le vecteur $(\beta_0,\ldots,\beta_K)$ et $x i$ le vecteur $(1,x_{1,i},\ldots,x_{K,i})$ , on peut réécrire le modèle de la manière suivante^[3] :

$y i = x i'β + u i$

La notation matricielle

Enfin, on rencontre aussi souvent une notation matricielle^[4] :

$y = X β + u$ avec $y = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}, \quad X = \begin{pmatrix} x'_1 \\ x'_2 \\ \vdots \\ x'_n \end{pmatrix} = \begin{pmatrix} 1 & x_{11} & \cdots & x_{1p} \\ 1 & x_{21} & \cdots & x_{2p} \\ \vdots & \ddots & \vdots \\ 1 & x_{n1} & \cdots & x_{np} \end{pmatrix}, \quad \beta = \begin{pmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_p \end{pmatrix}, \quad u = \begin{pmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{pmatrix}.$

Terminologie

Le modèle linéaire est utilisé dans un grand nombre de champs disciplinaires. Il en résulte une grande variété dans la terminologie. Soit le modèle suivant :

$y = \beta_0 + \beta_1 x_1 + \ldots + \beta_K x_K + u$

La variable y est appelée variable expliquée ou variable endogène. Les variables $(x_1,x_2,\ldots,x_K)$ sont appelées variables explicatives, variables exogènes ou encore prédicteurs. u est appelé terme d'erreur ou perturbation.

On note généralement $\hat \beta$ le vecteur des paramètres estimés. On définit la valeur prédite $\hat y_i = x_i \hat \beta$ et le résidu $\hat u_i = y_i - \hat y_i$ .

Les principales hypothèses

H1 L'hypothèse d'exogénéité

En notation vectorielle :

$\mathbb E (u_i|x_i) = 0$

En notation matricielle :

$\mathbb E (u | X) = 0$

H2 L'hypothèse de non colinéarité des variables explicatives

En notation vectorielle :

$\mathbb E (x_ix_i')$ inversible avec $x i'$ la transposée du vecteur $x i$

En notation matricielle :

$\mathbb E (X'X)$ inversible avec $X'$ la transposée de la matrice $X$ .

H3 L'hypothèse de non corrélation des résidus

$\forall i \neq j \quad \mathbb E(u_i u_j|x_i) = 0$

H4 L'hypothèse d'homoscédasticité

$\forall i \quad \mathbb E(u_i^2|x_i) = \sigma^2$

Si les deux précédentes hypothèses sont vérifiées, on peut écrire sous forme matricielle : $\mathbb V(u|X) = \sigma^2 I_n$ avec $I n$ la matrice identité de taille n.

H5 L'hypothèse de normalité des termes d'erreur

$u_i | x_i \sim \mathcal N (0, \sigma^2)$

Sous forme matricielle :

$u | X \sim \mathcal N (0, \sigma^2 I_n)$

Le modèle linéaire simple

Modèle de régression linéaire simple

On appelle généralement modèle linéaire simple un modèle de régression linéaire avec une seule variable explicative. Ce modèle est souvent présenté dans les manuels de statistiques à des fins pédagogiques.

$y i = β 0 + β 1 x i + u i$

Estimateur des moindres carrés ordinaires

L'estimateur des moindres carrés ordinaires est la solution du programme de minimisation de la somme des carrés des écarts entre les valeurs prédites et les valeurs observées par rapport aux deux paramètres $b 0$ et $b 1$ :

$\text{Argmin}_{b_0,b_1} \sum_{i = 1}^n (y_i - b_0 x_i - b_1)^2$

Le modèle standard

On appelle modèle standard un modèle dans lequel les hypothèses d'exogénéité (H1), de non colinéarité (H2), de non corrélation des termes d'erreur (H3) et d'homoscédasticité sont respectées (H4).

Estimation du modèle

Ce modèle peut être estimé par la méthode des moindres carrés ordinaires.

L'estimateur des moindres carrés ordinaires peut s'écrire $\hat\beta = \big(\, \tfrac{1}{n}{\textstyle\sum} x_i x'_i \,\big)^{-1} \big(\, \tfrac{1}{n}{\textstyle\sum} x_i y_i \,\big)$ sous forme vectorielle ou $\hat \beta = (X'X)^{-1} X'y$ sous forme matricielle^[4].

D'après le Théorème de Gauss-Markov, l'estimateur des moindres carrés ordinaires est le meilleur estimateur linéaire sans biais^[5].

Sous l'hypothèse de normalité des termes d'erreur (H5), l'estimateur des moindres carrés est aussi l'estimateur du maximum de vraisemblance^[5].

Le modèle avec corrélations des termes d'erreur ou hétéroscédasticité

Il arrive souvent que les hypothèses H3 et H4 ne soient pas vérifiées. On distingue alors deux cas : le cas où l'on peut faire des hypothèses raisonnables sur la matrice de variance-covariance du vecteur des perturbations et le cas où on ne fait aucune hypothèse sur cette matrice.

Estimation du modèle par les moindres carrés généralisés

Si on note $Ω$ la matrice de variance-covariance du vecteur des perturbations $u$ , on peut définir l'estimateur des moindres carrés généralisés : $\hat\beta = (X'\Omega^{-1}X)^{-1}X'\Omega^{-1}y,$

Estimation du modèle par les moindres carrés quasi-généralisés

Le modèle à variables instrumentales

Lorsque l'une des variables explicatives est corrélée au terme d'erreur (H1 violée), alors on peut avoir recours aux variables instrumentales. On appelle variable instrumentale une variable z qui a un effet sur les variables explicatives suspectées d'endogénéité mais n'est pas corrélée avec le terme d'erreur.

Lorsque l'hypothèse H1 d'exogénéité n'est pas crédible, on peut utiliser la méthode des variables instrumentales. Dans ce cas, il faut trouver un ensemble de variables dites instrumentales qui doivent être à la fois exogènes et corrélées aux variables explicatives du modèle. On note souvent le vecteur des variables instrumentales $z i$ et la matrice des variables instrumentales $Z$ .

Formellement, on introduit donc deux nouvelles hypothèses :

L'hypothèse d'exogénéité des instruments : $\mathbb E (u_i|z_i) = 0$ sous forme vectorielle ou $\mathbb E (u | Z) = 0$ sous forme matricielle.
Condition de rang : Z doit être corrélé à X.

Application

Très souvent utilisé en économétrie, le modèle à variables instrumentales est aussi utilisé en sciences politiques^[6].

Estimation du modèle par la méthode des doubles moindres carrés

Ce modèle peut être estimé par la méthode des doubles moindres carrés et dans ce cas, on obtient : $\hat\beta = [X'Z(Z'Z)^{-1}Z'X]^{-1}X'Z(Z'Z)^{-1}Z'y$ ^[7].

Extensions

Le modèle linéaire généralisé est une extension du modèle linéaire dans laquelle on pose $y_i = g^{-1} (\beta_0 + \beta_1 x_x + \ldots + x_K) + u_i$ . Cette classe de modèles comprend le modèle linéaire , le modèle de régression logistique, le modèle de Poisson, etc.
Le modèle linéaire hiérarchique ou modèle linéaire multiniveau est un modèle dans lequel il y a au moins deux niveaux d'observations, par exemple la région et les individus et dans lequel on va permettre aux coefficients de varier. Par exemple, le modèle suivant est un modèle linéaire hiérarchique : $y_{j,i} = \beta_{0,j} + \beta_{1,j} x_{1,j,i} + \ldots + \beta_{K,j} x_{K,j,i} + u_{j,i}$ .

Le modèle de régression quantile linéaire.

Le modèle additif généralisé

Le modèle Tobit pour traiter les variables censurées.

Le modèle de sélection ou modèle Heckit

Les modèles à équations simultanées

Références

↑ (en) Francis Galton, « Regression Towards Mediocrity in Hereditary Stature », dans Journal of the Anthropological Institute, vol. 15, 1886, p. 246-263 [texte intégral]
↑ Cameron et Trivedi 2005, Angrist et Pischke 2008, ...
↑ Cameron et Trivedi 2005, p. 70
↑ ^{a et b} Cameron et Trivedi 2005, p. 71
↑ ^{a et b} Wasserman 2004, Chapitre 13
↑ (en) Allison Sovey et Donald Green, « Instrumental Variables Estimation in Political Science: A Readers’ Guide », dans American Journal of Political Science, vol. 55, n^o 1, janvier 2011, p. 188-200
↑ Cameron et Trivedi 2005, p. 101

Bibliographie

(en) Francis Galton, « Regression Towards Mediocrity in Hereditary Stature », dans Journal of the Anthropological Institute, vol. 15, 1886, p. 246-263 [texte intégral]
Michel Armatte, Histoire du modèle linéaire. Formes et usages en statistique et en économétrie jusqu’en 1945, 1995, thèse EHESS sous la direction de Jacques Mairesse.

Manuels

(en) Larry Wasserman, All of Statistics : A Concise Course in Statistical Inference, New York, Springer-Verlag, 15 septembre 2004, 461 p. (ISBN 978-0387402727), p. chapitre 13
(en) Joshua Angrist et Jörn-Steffen Pischke, Mostly Harmless Econometrics : An Empiricist's Companion, Princeton University Press, 2008, 392 p. (ISBN 978-0691120355)
(en) Colin Cameron et Pravin Trivedi, Microeconometrics: Methods And Applications, Cambridge University Press, 2005, 1056 p. (ISBN 978-0521848053)

Voir aussi

Liens externes

v · Probabilités et statistiques

Théorie des probabilités

Axiomes des probabilités • Espace probabilisable • Probabilité • Événement • Tribu • Indépendance

Probabilités élémentaires	Moyenne • Espérance • Médiane • Variance • Écart type
Loi de probabilité	Variable aléatoire • Loi de Bernoulli • Loi de Poisson • Loi uniforme • Loi normale • Loi de Student • Loi de Fisher • Variables iid
Convergence de lois	Théorème central limite • Loi des grands nombres • Théorème de Borel-Cantelli
Calcul stochastique	Marche aléatoire • Chaîne de Markov • Processus stochastique • Processus de Markov • Martingale • Mouvement brownien • Équation différentielle stochastique

Statistiques

Statistique descriptive	Échantillon • Quantile • Intervalle de confiance • Représentations de données • Histogramme • Diagramme circulaire • Boîte à moustaches • Régression linéaire • Méthode des moindres carrés
Statistique mathématique	Fonction de répartition empirique • Théorème de Glivenko-Cantelli • Inférence bayésienne
Tests statistiques	Test d'hypothèse • Hypothèse statistique • Estimateur • Test du χ² • Test t • Test de Fisher

Applications

Économétrie • Mécanique statistique • Jeu de hasard • Biomathématique • Mathématiques financières

Portail de l’économie
Portail des probabilités et des statistiques

Catégories :

Estimation (statistique)
Économétrie
Statistiques

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Régression linéaire de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Regression lineaire — Régression linéaire Pour les articles homonymes, voir Régression. Un exemple graphique En statistiques, étant donné un échantillon aléatoire … Wikipédia en Français
Regression lineaire multiple — Régression linéaire multiple Pour les articles homonymes, voir Régression. Sommaire 1 Modèle théorique 1.1 Exemple 1.2 E … Wikipédia en Français
Régression linéaire multiple — Pour les articles homonymes, voir Régression. La régression linéaire multiple est une analyse statistique qui décrit les variations d une variable endogène associée aux variations de plusieurs variables exogènes. Par exemple, une analyse de… … Wikipédia en Français
Régression multilinéaire — Régression linéaire multiple Pour les articles homonymes, voir Régression. Sommaire 1 Modèle théorique 1.1 Exemple 1.2 E … Wikipédia en Français
Regréssion fallacieuse — Régression fallacieuse Pour les articles homonymes, voir Régression. La régression fallacieuse désigne une situation dans laquelle l utilisation de séries temporelles non stationnaires dans une régression linéaire fait apparaître des résultats… … Wikipédia en Français
Regression logistique — Régression logistique Pour les articles homonymes, voir Régression. La régression logistique est une technique statistique qui a pour objectif, à partir d’un fichier d’observations, de produire un modèle permettant de prédire les valeurs prises… … Wikipédia en Français
Regression (statistiques) — Régression (statistiques) Pour les articles homonymes, voir Régression. La régression est une méthode statistique très utilisée pour analyser la relation d une variable par rapport à une ou plusieurs autres. On recourt à une estimation des… … Wikipédia en Français
Régression mathématique — Régression (statistiques) Pour les articles homonymes, voir Régression. La régression est une méthode statistique très utilisée pour analyser la relation d une variable par rapport à une ou plusieurs autres. On recourt à une estimation des… … Wikipédia en Français
Regression — Régression Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Régression fallacieuse — Pour les articles homonymes, voir Régression. La régression fallacieuse désigne une situation dans laquelle l utilisation de séries temporelles non stationnaires dans une régression linéaire fait apparaître des résultats erronés, trop optimistes … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Régression linéaire

Sommaire

Histoire