Dérivation vectorielle

Dans l'espace euclidien, c'est-à-dire dans un repère quelconque Oxyz muni de vecteurs unitaires $\vec{i}, \vec{j}, \vec{k} \;$ , une fonction vectorielle est représentée $\vec{V} \;$ . Ses trois coordonnées (ou composantes scalaires) $X, Y et Z \;$ sont fonction de la variable réelle $t \;$ . On dit que $\vec{V} \;$ est une fonction réelle de $t \;$ . Dans ce qui suit, on conviendra que la fonction vectorielle est représentée par la symbolique : $\vec{V{(t)}} \;$

Sommaire

1 Limite d'une fonction vectorielle
2 Accroissement d'une fonction vectorielle
3 Continuité
4 Dérivée vectorielle
- 4.1 Théorème
- 4.2 Interprétation géométrique
5 Principales formules de dérivation
6 Développement limité
7 Voir aussi

Limite d'une fonction vectorielle

Limite nulle : $\vec{V{(t)}} \;$ tend vers $\vec{0} \;$ quand $t \;$ tend vers $t_0 \;$ si les coordonnées $X, Y et Z \;$ de $\vec{V} \;$ tendent vers 0 quand $t \;$ tend vers $t_0 \;$

Dans ces conditions :

$\vec{V} \rightarrow \vec{0}$

implique que :

$X \rightarrow 0, Y \rightarrow 0 , Z \rightarrow 0$

Limite quelconque : Soit une fonction vectorielle $\vec{V_t} = \begin{pmatrix} X \\ Y \\ Z \end{pmatrix}$ et un vecteur $\vec{V_0} = \begin{pmatrix} X_0 \\ Y_0 \\ Z_0 \end{pmatrix}$

$\vec{V{(t)}} \;$ tend vers $\vec{V_0} \;$ quand $t \;$ tend vers $t_0 \;$ à condition que la différence $\vec{V{(t)}} - \vec{V_0} \rightarrow \vec{0} \;$

Dans ces conditions :

$\vec{V{(t)}} \rightarrow \vec{V_0} \;$

donc :

$X - X_0 \rightarrow 0, Y - Y_0 \rightarrow 0 , Z - Z_0 \rightarrow 0$

implique que :

$X \rightarrow X_0, Y \rightarrow Y_0 , Z \rightarrow Z_0$

Propriétés des limites : La limite d'une fonction vectorielle est unique et ne dépend pas du choix du repère : Si, lorsque : $t \rightarrow t_0$ , les fonctions vectorielles $\vec{U_t}$ et $\vec{V_t}$ tendent vers $\vec{U_0}$ et $\vec{V_0}$ :

$\vec{U_t} + \vec{V_t}$ tend vers $\vec{U_0} + \vec{V_0}$ ,

$\alpha(t) \vec{U_t}$ tend vers $\alpha_0 \vec{U_0}$

avec

$\alpha_0 = \lim_{t \to t_0}\alpha(t)$ .

Accroissement d'une fonction vectorielle

Soit $\Delta t = t - t_0 \;$ l'accroissement de la variable t. On désigne par accroissement de la fonction vectorielle $\vec{V{(t)}} \;$ la différence :

$\vec{V{(t)}} - \vec{V{(t_0)}} \;$

que l'on note

$\Delta\vec{V{(t)}}$

ses coordonnées sont :

$\Delta X = X(t) - X(t_0)\;$ ,

$\Delta Y = Y(t) - X(t_0)\;$ ,

$\Delta Z = Z(t) - X(t_0)\;$ .

Donc :

$\Delta\vec{V{(t)}} = \Delta X_\vec{i} + \Delta Y_\vec{j} + \Delta Z_\vec{k}$

Continuité

Lorsque $\Delta\vec{V} = \vec{V{(t)}} - \vec{V{(t_0)}}$ tend vers zéro quand $\Delta\ t$ tend vers zéro.

alors $\vec{V{(t)}} \;$ est continue pour $t = t_0 \;$

Conclusion :

$\vec{V{(t)}}$ continue pour $t = t_0 \Leftrightarrow \Delta\vec{V} \rightarrow \vec{0}$ quand $\Delta\ t \rightarrow 0$

Dérivée vectorielle

La fonction vectorielle $\vec{V{(t)}} \;$ admet une dérivée en $t = t_0 \;$ lorsque le rapport $\frac{\Delta\vec{V}}{\Delta\ t}\,$ tend vers un vecteur limite lorsque $\Delta\ t \;$ tend vers zéro.

Ce vecteur limite, noté, $\vec{V'{(t_0)}} \;$ est le vecteur dérivé.

Lorsque $\vec{V{(t)}} \;$ est dérivable sur un intevalle, on désigne par $\vec{V'{(t)}} \;$ ou $\vec{V'} \;$ la fonction vectorielle ainsi obtenue.

Ses composantes sont $X'(t), Y'(t), Z'(t) \;$ ou encore $X', Y', Z' \;$ .

Coordonnées de $\vec{V'{(t)}} \;$ :

Les coordonnées de $\frac{\Delta\vec{V}}{\Delta\ t} \;$ sont $\frac{\Delta\ X}{\Delta\ t}, \frac{\Delta\ Y}{\Delta\ t}, \frac{\Delta\ Z}{\Delta\ t} \;$ .

Comme $\frac{\Delta\vec{V}}{\Delta\ t} \rightarrow \vec{V'{(t)}} \Leftrightarrow \frac{\Delta\ X}{\Delta\ t} \rightarrow X' , \frac{\Delta\ Y}{\Delta\ t} \rightarrow Y' , \frac{\Delta\ Z}{\Delta\ t} \rightarrow Z'\;$ .

Théorème

Un vecteur $\vec{V{(X,Y,Z)}} \;$ , fonction de $t \;$ , admet un vecteur dérivé $\vec{V'{(X',Y',Z')}} \;$ si et seulement si les coordonnées $X,Y,Z \;$ admettent pour dérivées les coordonnées $X',Y',Z' \;$

Si $\vec{V'} \;$ existe alors $\vec{V} = X\vec{i} + Y\vec{j} + Z\vec{k} \Leftrightarrow \vec{V'} = X'\vec{i} + Y'\vec{j} + Z'\vec{k} \;$

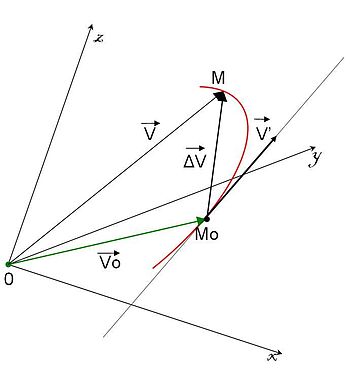
Interprétation géométrique

Fig.1. Représentation géométrique du vecteur dérivé V'.

Soit un repère quelconque Oxyz et considérons M, un point courant d'une courbe C d'équation paramétrique fonction de t.

Supposons :

$\vec{V} = \vec{OM} \;$ dérivable pour $t = t_0 \;$

et sa dérivée en $t_0 \;$

$\vec{V'}\not=\vec{0} \;$

Considérons les vecteurs

$\vec{OM_0}=\vec{V_0} \;$ ,

$\vec{OM}=\vec{V} \;$ ,

on a :

$\Delta\vec{V} = \vec{V} - \vec{V_0} = \vec{OM} - \vec{OM_0}\;$

Le vecteur

$\frac{\Delta\vec{V}}{\Delta\ t} = \frac{\Delta\vec{M_0M}}{\Delta\ t} \;$ est porté par la droite $M_0M \;$ (sécante à la courbe C lieu de M).

Lorsque $\Delta\ t \rightarrow 0, \vec{MM_0} \rightarrow \vec{0} \;$ autrement dit le points $M \;$ tend à se confondre avec et $M_0 \;$ et la droite $MM_0 \;$ a pour limite le support de $\vec{V'} \;$ .

On dit que la courbe C admet une tangente au point $M_0 \;$ , et le vecteur dérivé $\vec{V'} \;$ est porté par cette tangente.

Principales formules de dérivation

Soit deux vecteurs :

$\vec{V_1} = \begin{pmatrix} X_1 \\ Y_1 \\ Z_1 \end{pmatrix}$ et $\vec{V_2} = \begin{pmatrix} X_2 \\ Y_2 \\ Z_2 \end{pmatrix}$

admettant les dérivées par rapport à la variable $t$ :

$\vec{V'_1} = \begin{pmatrix} X'_1 \\ Y'_1 \\ Z'_1 \end{pmatrix}$ et $\vec{V'_2} = \begin{pmatrix} X'_2 \\ Y'_2 \\ Z'_2 \end{pmatrix}$

Dérivée de la somme vectorielle

Le vecteur :

$\vec{V_1} + \vec{V_2}$

a pour coordonnées :

$\begin{pmatrix} X_1 + X_2 \\ Y_1+Y_2 \\ Z_1+Z_2 \end{pmatrix}$

qui admettent pour dérivée :

$\begin{pmatrix} X'_1 + X'_2 \\ Y'_1+Y'_2 \\ Z'_1+Z'_2 \end{pmatrix}$ qui sont les coordonnées du vecteur $\vec{V'_1} + \vec{V'_2}$ .

Donc $(\vec{V_1} + \vec{V_2})' = \vec{V'_1} + \vec{V'_2}$

Dérivée du produit d'un vecteur par un scalaire

Soit

$\vec{V_1(t)} \;$

$\alpha(t) \;$

tous deux supposés dérivables. Le vecteur :

$\alpha \vec{V_1} \;$

a pour coordonnées :

$\begin{pmatrix} \alpha X_1 \\ \alpha Y_1 \\ \alpha Z_1 \end{pmatrix}$

qui admettent pour dérivées

$\begin{pmatrix} \alpha' X_1 + \alpha X'_1 \\ \alpha' Y_1 + \alpha Y'_1 \\ \alpha' Z_1 + \alpha Z'_1 \end{pmatrix}$ qui sont les coordonnées du vecteur $\alpha' \vec{V_1} + \alpha \vec{V'_1}$ .

Donc $(\alpha \vec{V_1})' = \alpha' \vec{V_1} + \alpha \vec{V'_1}$

Dérivée d'une fonction vectorielle de fonction numérique

Soit :

$\vec{V(f)} \;$ , une fonction vectorielle dérivable,

$f(t) \;$ une fonction numérique dérivable.

Alors $(\vec{V(f(t))})' = \vec{V'(f)}.f'(t) \;$

Dérivée du produit scalaire

Soit deux vecteurs dérivable :

$\vec{U}$ et $\vec{V}$

Soit le scalaire :

$\vec{U}.\vec{V}$ ,

Alors $(\vec{U}.\vec{V})' = \vec{U'}.\vec{V} + \vec{U}.\vec{V'}\;$

Dérivée d'un carré scalaire :

$(\vec{V}^2)' = 2\vec{V}.\vec{V'}$ ,

En dérivant les deux membres de l'égalité suivante :

$\|\vec{V}^2\| = \vec{V}^2$ ,

On obtient :

$2\|\vec{V}\|.\|\vec{V'}\| = 2\vec{V}.\vec{V'}$

D'où l'on tire :

$\|\vec{V'}\| = \frac{\vec{V}}{\|\vec{V}\|} \vec{V'}$

Avec $\frac{\vec{V}}{\|\vec{V}\|} = \vec{u}$ représentant le vecteur unitaire de $\vec{V}$ ; on observe que :

$\|\vec{V'}\| = \vec{u}.\vec{V'}$

On retiendra que

$\vec{u}.\vec{V'}$

représente la mesure algébrique de la projection de $\vec{V'}$ sur la droite directrice support de $\vec{V}$ .

Dérivée d'un vecteur unitaire

Soit un vecteur unitaire définit comme suit :

$\vec{u} = \begin{pmatrix} \cos \alpha \\ \sin \alpha \end{pmatrix}$

Les coordonnées de ce vecteur dérivé sont :

$\vec{u'} = \begin{pmatrix} -\sin \alpha \\ \cos \alpha \end{pmatrix} = \begin{pmatrix} \cos (\alpha + \frac{\pi}{2}) \\ \sin (\alpha + \frac{\pi}{2}) \end{pmatrix}$

On observe que :

$\vec{u'}$ est perpendiculaire $\vec{u}$

Par récurrence :

$\vec{u''}$ est perpendiculaire $\vec{u'}$

On en déduit que :

$\vec{u''} = -\vec{u}$

D'où une expression de la dérivée d'ordre n comme suit :

$\vec{u^{n}} = \begin{pmatrix} \cos (\alpha + n\frac{\pi}{2}) \\ \sin (\alpha + n\frac{\pi}{2}) \end{pmatrix}$

Dérivée du produit vectoriel

Soit deux vecteurs dérivables :

$\vec{U}$ et $\vec{V}$

Soit le vecteur :

$\vec{U}\wedge\vec{V}$

sa dérivée est : $(\vec{U}\wedge\vec{V})' = \vec{U'}\wedge\vec{V} + \vec{U}\wedge\vec{V'}\;$

Développement limité

Voir aussi

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Dérivation vectorielle de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Dérivation lagrangienne — Concepts de base en théorie des milieux continus Cet article traite des concepts de base en théorie des milieux continus. De nombreux articles de Wikipédia traitent de milieux continus dans le cadre de différents domaines de la physique :… … Wikipédia en Français
Dérivation (mathématiques élémentaires) — Dérivée Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… … Wikipédia en Français
Dérivation partielle — Dérivée partielle En mathématiques, la dérivée partielle d une fonction est la dérivée par rapport à l une de ses variables, les autres étant gardées constantes. Cette approche est utile dans l analyse en dimension n, la géométrie différentielle … Wikipédia en Français
Divergence (analyse vectorielle) — Pour les articles homonymes, voir Divergence. En géométrie, la divergence d un champ de vecteurs X mesure le défaut à ce que son flot préserve une forme volume Ω. La divergence de X, notée div X, est une fonction à valeurs réelles qui mesure la… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Produit vectoriel — En mathématiques, et plus précisément en géométrie, le produit vectoriel est une opération vectorielle effectuée dans les espaces euclidiens orientés de dimension trois[1],[2]. Le formalisme utilisé actuellement est apparu en 1881 dans un manuel… … Wikipédia en Français
Calcul vectoriel en géométrie euclidienne — Cet article traite des opérations portant sur les vecteurs en géométrie euclidienne. Sommaire 1 Opérations sur les vecteurs dans le plan et l espace 1.1 Produit d un vecteur par un scalaire 1.2 Somme de deux vecteurs … Wikipédia en Français
Produit scalaire — En géométrie vectorielle, le produit scalaire est une opération algébrique s ajoutant aux lois s appliquant aux vecteurs. À deux vecteurs elle associe leur produit, qui est un nombre réel (ou scalaire). Elle permet d exploiter les notions de la… … Wikipédia en Français
Cinématique — Pour l emploi du terme dans le domaine du jeu vidéo, voir Scène cinématique. En physique, la cinématique est la discipline de la mécanique qui étudie le mouvement des corps, en faisant abstraction des causes du mouvement (celles ci sont… … Wikipédia en Français
Mécanique analytique — La mécanique classique peut être écrite (formalisée) de différentes manières. La plus courante est la formulation de Newton, qui utilise la notion de force : elle est de loin la plus simple lorsqu il s agit de considérer un problème concret… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Dérivation vectorielle

Sommaire

Limite d'une fonction vectorielle

Accroissement d'une fonction vectorielle

Continuité