Hauteurs d'un triangle

On appelle hauteurs d'un triangle chacune des trois droites passant par un sommet du triangle et perpendiculaire au côté opposé à ce sommet. Les pieds des hauteurs sont les projetés orthogonaux de chacun des sommets sur le côté opposé.

Orthocentre

Les trois hauteurs d'un triangle sont concourantes. Leur point d'intersection H, est nommé orthocentre du triangle.

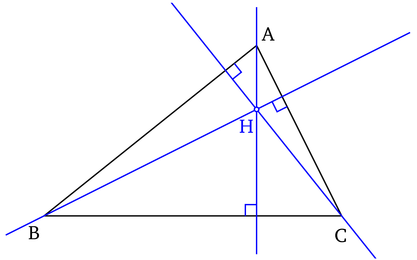Hauteurs et orthocentre d'un triangle

L'orthocentre est le barycentre des points pondérés [A, tan(Â)] ; [B, tan(B)] ; [C, tan(C)].

Symétriques de l'orthocentre

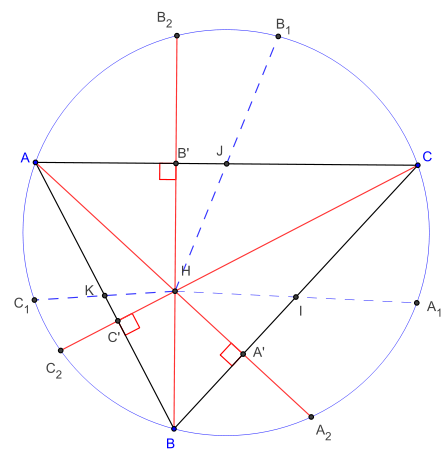
Les symétriques A₁, B₁ et C₁ de l'orthocentre H par rapport aux milieux des côtés du triangle se trouvent sur le cercle circonscrit.
Les symétriques orthogonaux A₂, B₂ et C₂ de l'orthocentre par rapport aux côtés du triangle se trouvent également sur le cercle circonscrit.

Symétriques de l'orthocentre par rapport aux milieux des côtés et par rapport aux côtés du triangle

Démonstration avec des homothéties : voir cercle d'Euler.

Cercle de Taylor

Soit A', B' et C' les pieds des hauteurs du triangle. On note A₂ et A₃ les projetés orthogonaux de A' sur les côtés AB et AC du triangle et on définit de même B₂ et B₃ par rapport à B' et C₂ et C₃ par rapport à C'. Les six points ainsi définis sont cocycliques : ils sont situés sur le cercle de Taylor du triangle.

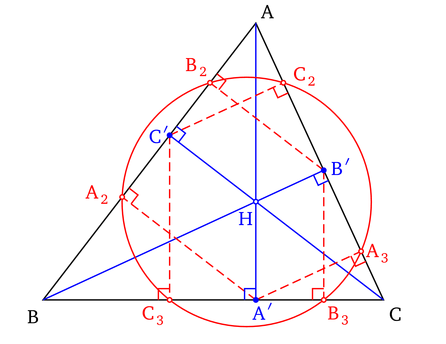Cercle de Taylor d'un triangle

On a : (A₂A₃, BC) = (AB, AC), la droite (A₂A₃) est antiparallèle de (BC) par rapport à (AB) et (AC), et des propriétés analogues pour (B₂B₃) et (C₂C₃).

(B₂C₂) est parallèle à (BC). De même (A₂C₃) //(AC) et (A₃B₃)//(AB).

C'est la configuration d'un cercle de Tücker particulier, dit cercle de Taylor.

On trouve A₂A₃ = B₂B₃ = C₂C₃.

L'hexagone ayant pour sommets ces six projections est l'hexagone de Catalan (mathématicien belge 1814-1894).

Centre du cercle de Taylor

Les trois droites (A₁A₂), (B₁B₂) et (C₁C₂) joignant les projections sont parallèles aux côtés du triangle orthique et coupent ses côtés en leurs milieux P, Q et R. Ces droites déterminent le côtés du triangle PQR qui est le triangle médian du triangle orthique.

Si le triangle ABC est acutangle alors le centre du cercle de Taylor est le centre du cercle inscrit dans le triangle médian du triangle orthique.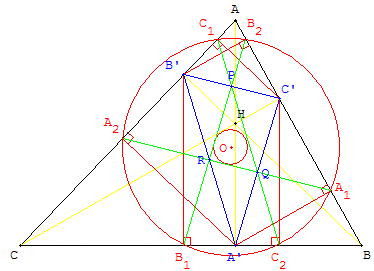

Centre du cercle de Taylor d'un triangle acutangle

Si le triangle ABC est obtus alors le centre du cercle de Taylor est un des centre des cercles exinscrits du triangle PQR. Plus précisément, si ABC est obtus en A (respectivement en B, en C), alors le centre du cercle de Taylor est le centre du cercle exinscrit à PQR dans l'angle de sommet P, milieu de [B’C’] (respectivement Q milieu de [C’A’] , R milieu de [A’B’]).

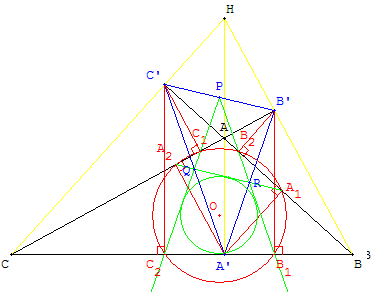Centre du cercle de Taylor d'un triangle obtus en A

Axe orthique

Dans un triangle ABC, soit A' (respectivement B' et C') le pied de la hauteur issue de A (respectivement issue de B et de C).

A₁, B₁ et C₁ sont les trois autres points d'intersection des côtés du triangle ABC et de ceux du triangle orthique A’B’C’ : on note A₁ l'intersection de (BC) et de (A'B'), B₁ l'intersection de (AC) et de (A'C'), C₁ l'intersection de (AB) et de A'B').

Les trois points A₁, B₁ et C₁ sont alignés sur une droite dénommée l'axe orthique du triangle.

L'axe orthique est aussi l'axe radical du cercle circonscrit et du cercle d'Euler.

La droite d'Euler, ligne des centres des deux cercles, est perpendiculaire à l'axe.

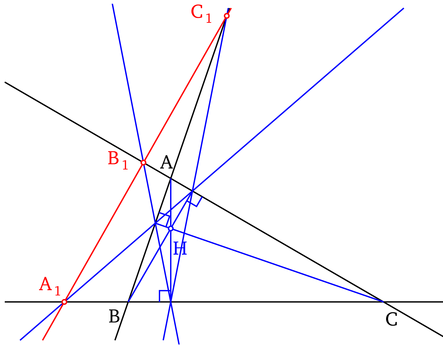Axe orthique d'un triangle

Démonstrations et références

• Revue Quadrature, Janvier-Mars 2007
• La géométrie du triangle

Articles connexes

• Triangle
• Triangle orthique
• Cercle d'Euler

• Portail de la géométrie