- Aire De Surfaces Usuelles
-
Aire de surfaces usuelles
La notion d'aire d'une surface se définit en géométrie euclidienne en dimension 2 ou 3 et est supposée connue du lecteur. L'aire des surfaces usuelles s'exprime à l'aide de formules simples. On peut estimer l'aire d'une surface aux contours compliqués en sommant des aires de surfaces plus simples. Ce point de vue débouche sur le calcul des intégrales. Le théorème de Guldin permet de calculer aisément l'aire de surfaces de révolution.
Surfaces planes
Nom de la surface Description Paramètres Aire Carré Quadrilatère aux angles et côtés égaux Longueur a d'un des côtés a2 Rectangle Quadrilatère aux angles droits Longueurs a et b des côtés ab Triangle Donnée de trois points A B C non colinéaires du plan Hauteur h en B et longueur b du segment opposé [AC] 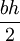
Longueurs a, b et c des côtés et demi-périmètre s 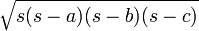 (Formule de Héron)
(Formule de Héron)Trapèze Quadrilatère possédant deux côtés opposés parallèles, ses bases Longueur a et b des bases et distance h entre elles 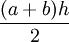
Losange Quadrilatère ayant ses quatre côtés de même longueur et parallèles deux à deux. Longueurs a et b de ses diagonales 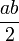
Parallélogramme Quadrilatère dont les côtés opposés sont parallèles Longueurs a et b des côtés adjacents et mesure θ de l'angle qu'ils forment absin(θ) Longueur b d'un côté du parallélogramme et longueur h de la hauteur associée bh Disque Ensemble des points à une distance du centre inférieure ou égale au rayon Rayon r πr2 Ellipse Ensemble des points tels que la somme de leurs distances à deux points fixes, dits foyers, est constante Longueurs a et b des demi-axes πab Surfaces à trois dimensions
Nom de la surface Description Paramètres Aire Cube Longueur a d'un des côtés 6a2 Parallélépipède rectangle Longueurs a b et c des côtés 2(ab + bc + ca) Sphère Rayon R 4πR2 Calotte ou zone sphérique Rayon R et hauteur H 2πRH Tore Rayons R > r 4π2aR Cylindre Rayon R et hauteur h 2πRh + 2πR2 Sphéroïde prolate ellipsoïde de demi-axes (a,b,b) , a > b 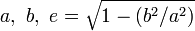
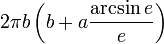
Sphéroïde oblate ellipsoïde de demi-axes (b,a,a) , a > b 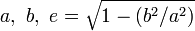
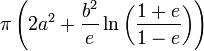
Voir aussi
- Portail de la géométrie
Catégories : Aire | Surface
Wikimedia Foundation. 2010.
