Angles alternes-internes
- Angles alternes-internes
-
En géométrie, deux droites coupées par une sécante forment des angles dont les sommets sont aux points d'intersection.
Définition
Deux angles formés par deux droites coupées par une sécante sont dits angles alternes-internes si :
- ils sont situés de part et d'autre de la sécante ;
- ils sont situés entre les deux droites ;
- ils ne sont pas angles adjacents.
Droites quelconques
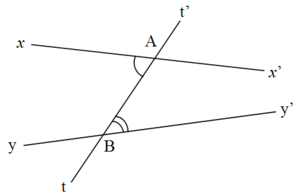
Les droites (xx') et (yy') sont coupées respectivement en A et en B par la sécante (tt').propriété numero 1
et 
sont des angles alternes-internes.
Droites parallèles
- Propriété
- Si deux droites parallèles sont coupées par une sécante, alors ces droites forment des angles alternes-internes de même mesure.
- Réciproquement, si deux droites coupées par une sécante forment des angles alternes-internes de même mesure, alors ces deux droites sont parallèles.
- Exemple
Sur la figure suivante, les droites a et b sont parallèles, s est une sécante quelconque.
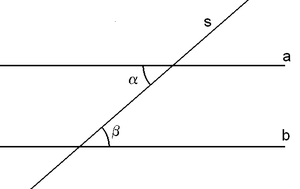α et β sont des angles alternes-internes égaux .
Voir aussi
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Angles alternes-internes de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Angles alternes-externes — En géométrie, lorsque deux droites sont coupées par une sécante, il se forme des angles dont les sommets sont aux points d intersection. Deux angles sont dits angles alternes externes si : ils sont situés de part et d autre de la sécante,… … Wikipédia en Français
Angles Alterne-interne — Angles alternes internes En géométrie, deux droites coupées par une sécante forment des angles dont les sommets sont aux points d intersection. Sommaire 1 Définition 2 Droites quelconques 3 Droites parallèles … Wikipédia en Français
Angles alterne-interne — Angles alternes internes En géométrie, deux droites coupées par une sécante forment des angles dont les sommets sont aux points d intersection. Sommaire 1 Définition 2 Droites quelconques 3 Droites parallèles … Wikipédia en Français
Angles Alterne-externe — Angles alternes externes En géométrie, lorsque deux droites sont coupées par une sécante, il se forme des angles dont les sommets sont aux points d intersection. Deux angles sont dits angles alternes externes si : ils sont situés de part et… … Wikipédia en Français
Angles alterne-externe — Angles alternes externes En géométrie, lorsque deux droites sont coupées par une sécante, il se forme des angles dont les sommets sont aux points d intersection. Deux angles sont dits angles alternes externes si : ils sont situés de part et… … Wikipédia en Français
Angles Correspondants — En géométrie, lorsque deux droites sont coupées par une sécante, il se forme des angles dont les sommets sont aux points d intersection. Les angles correspondants sont isométriques lorsque les deux droites sont parallèles. Droites quelconques… … Wikipédia en Français
Angles correspondants — En géométrie, lorsque deux droites sont coupées par une sécante, il se forme des angles dont les sommets sont aux points d intersection. Les angles correspondants sont isométriques lorsque les deux droites sont parallèles. De plus, pour que deux… … Wikipédia en Français
Angles complémentaires — Pour les articles homonymes, voir Complémentaire. Ne doit pas être confondu avec Angles supplémentaires … Wikipédia en Français
Angles opposés par le sommet — Les angles α et γ sont opposés par le sommet, ainsi que les angles β et δ. En géométrie, deux angles sont dits angles opposés par le sommet si : ils ont le même sommet et les côtés de l un sont les prolongements des côtés de l autre. Les… … Wikipédia en Français
Angles supplémentaires — Pour les articles homonymes, voir Supplémentaire. Ne doit pas être confondu avec Angles complémentaires … Wikipédia en Français
