Norme (arithmétique)

Pour les articles homonymes, voir norme.

En mathématiques la norme est une notion utilisée en théorie de Galois ou en théorie algébrique des nombres.

La théorie classique de Galois étudie des extensions finies L d'un corps commutatif K en un autre corps commutatif. L'ensemble L contient K (ou, ce qui revient au même, il existe un morphisme de corps injectif de K dans L), L est commutatif et L, considéré comme un espace vectoriel sur le corps K est de dimension finie. Une première définition de la norme est l'application qui à un élément l de L associe le déterminant de la fonction multiplication par l.

En arithmétique, la norme relative est une application d'un sur-corps L vers un sous-corps K d'une extension. Cette application intervient de façon cruciale dans la théorie des corps de classes : les sous-extensions abéliennes d'une extension donnée sont essentiellement en correspondance avec des groupes de normes, c'est-à-dire l'image dans le sous-corps par la norme de certains groupes du sur-corps.

Cette notion s'étend en une notion de norme d'un idéal, définie pour les idéaux premiers comme le cardinal du corps résiduel, puis par multiplicativité, pour les idéaux composés. La norme d'un idéal principal est alors égale à la norme relative sur Q, l'ensemble des nombres rationnels, d'un générateur de cet idéal. La démonstration de la finitude du groupe des classes utilise des propriétés de majoration de la norme des idéaux dans une classe donnée.

Définitions

Soit K un corps commutatif, L une extension finie et l un élément de L. Une première définition est la suivante :

• La norme relative de l'élément l dans K est le déterminant de l'endomorphisme du K espace vectoriel L qui à x associe l.x. Cette norme est généralement notée N_L/K(l).

Il existe une définition plus restrictive et équivalente si les conditions d'existence sont remplies :

• Si l'extension L est galoisienne, la norme relative d'un élément l de L est le produit des images d'une racine du polynôme minimal par les différents automorphismes du groupe de Galois.

La norme d'un nombre algébrique peut être définie sans référence à la donnée d'une extension L, on parle alors de norme et non plus de norme relative.

• La norme d'un nombre α algébrique sur K est égale au coefficient constant de son polynôme minimal si le polynôme est séparable. Une telle norme est parfois notée N(α).

Cette définition s'applique encore si le nombre est un entier algébrique ; la norme est alors entière. Elle se généralise aux idéaux de l'anneau commutatif O_L des entiers algébriques d'un corps de nombres L :

• La norme d'un idéal M de O_L est le cardinal (fini) de l'anneau quotient O_L/M.

Propriétés

Théorie de Galois

Si les trois définitions semblent a priori éloignées les unes des autres, la réalité est différente :

• Si une extension finie L est galoisienne, le déterminant de l'application multiplication par l, où l est un élément de L est égal au produit des images d'une racine du polynôme minimal par les différents automorphismes du groupe de Galois.

L'article polynôme minimal d'un nombre algébrique montre que si σ₁, σ₂, ..., σ_d désigne les différents éléments du groupe de Galois, d étant la dimension de L en tant que K espace vectoriel et χ[X] le polynôme caractéristique, l'égalité suivante est vérifiée :

Le déterminant est égal au monôme constant du polynôme caractéristique, correspondant bien au produit des σ_i(m) pour i décrivant l'intervalle de borne 1 et d.

La définition d'une norme relative à une extension et d'une norme est un peu différente. Il suffit de considérer un élément k de K pour s'en rendre compte, sa norme relative est égal à k^d et sa norme à k.

• Soit l un élément de L et n la dimension de l'espace vectoriel L sur le corps de rupture K[l]. Si N(l) désigne la norme de l et N_L/K(l) sa norme relative, alors :

Ce résultat provient de l'égalité suivante, si P(X) désigne le polynôme minimal de l, démontrée dans l'article polynôme minimal d'un nombre algébrique :

Une propriété est vérifiée pour la norme relative :

• Soit l₁ et l₂ deux éléments de L, le produit des normes relatives de l₁ et l₂ est égal à la norme relative du produit l₁.l₂.

Cette propriété est la conséquence directe du fait que le produit de deux déterminants est égal au déterminant des produits. L'égalité n'est en général pas vraie pour les normes. Il n'existe en effet aucune raison pour que les corps de ruptures aient même dimension.

Théorie algébrique des nombres

Ici, K est une extension finie des nombres rationnels et L une extension finie de K. On considère deux anneaux O_K et O_L fermeture intégrale des corps K et L. Ce sont des anneaux de Dedekind. La norme considérée est la norme relative. Un cas particulier simple est étudié dans l'article Entier quadratique.

• La norme relative de L sur K d'un entier α de O_L est un entier de O_K.

Dire que α, un élément de L est entier sur K revient à dire que son polynôme minimal est à coefficients dans les entiers algébriques de O_K. Son polynôme caractéristique, puissance du polynôme minimal est aussi à coefficients dans les entiers de O_K, ce qui montre le caractère intégrale de la norme.

La norme relative dispose d'une propriété remarquable si K est égal à Q le corps des rationnels :

• La valeur absolue de la norme relative d'un entier algébrique α de L sur Q est égale au cardinal de l'anneau quotient O_L/ αO_L.

Illustration de l'anneau Z[³√2] en tant que réseau.

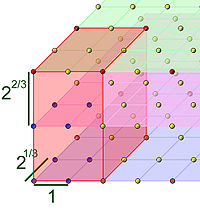
Cette propriété se démontre à l'aide de considérations issues de la géométrie arithmétique. Le corps L peut être vu comme un espace vectoriel sur Q. L'anneau O_L, qui admet une base B en tant que Z module peut être vu comme un réseau, c'est-à-dire comme un sous-groupe discret de L, composé des éléments de L à coefficients dans Z pour la base B. Cette représentation est illustrée sur la figure de droite pour l'exemple Z[³√2]. Une base de l'anneau est 1, ³√2 et ³√4. Les points de l'anneau correspondent aux vecteurs de Q[³√2] à coefficients entiers dans cette base. Ils sont représentés par les petites billes sur le schéma. L'idéal des multiples de α peut être vu comme l'image de l'application linéaire φ_α, qui à β, un élément de l'anneau, associe α.β. Dans l'exemple, on a choisi α égal à 2 et les points de l'idéal sont en rouge sur la figure. Il forme aussi un réseau de base α.B.

Le cœur du raisonnement consiste à étudier le volume cubique rouge du schéma. Il est composé des points de coordonnées comprises dans l'intervalle [0, 1[ dans la base α.B. Comme α.B est une base de l'idéal engendré par α (l'idéal est considéré comme un Z module) cette zone porte le nom de domaine fondamental. Si l'espace est muni d'un produit scalaire euclidien conférant à B le statut de base orthonormale, le volume du domaine fondamental, encore appelé volume fondamental, est égal à la valeur absolue du déterminant de φ_α, ou encore à la valeur absolue de la norme de α. Sur la figure, cette norme est égale à 8 car φ_α est une homothétie de rapport 2 dans un espace de dimension 3. Sur la figure, on remarque bien que le cube rouge est formé de 8 petits cubes de côté 1, (par définition du produit scalaire choisi, les vecteurs 1, ³√2 et ³√4 sont de longueur 1).

Ce domaine fondamental contient exactement autant de points de l'anneau que le cardinal du quotient O_L/ αO_L. Dans l'exemple, il est simple de s'en rendre compte. Si β est un point quelconque de O_L, il est congru au point dont les coordonnées sont le reste des divisions euclidiennes de celles de β par 2, modulo αO_L. Il existe donc un unique représentant d'une classe de O_L/ αO_L dans le domaine fondamental. Dans l'exemple, on remarque qu'il existe exactement 8 classes, dont les représentants dans le domaine fondamental sont les points de coordonnées 0 ou 1 dans la base B. Ils sont représentés en bleu sur la figure.

Le principe de la démonstration consiste à étudier le volume formé par l'union des cubes de côté 1 et de centre les points de l'anneau inclus dans le volume fondamental. Sur la figure, on obtient un volume correspondant au translaté du domaine fondamental par le vecteur -1/2(1 + ³√2 + ³√4). L'égalité de ce volume et du volume fondamental permet de conclure et justifie la définition suivante :

• Soit J un idéal de O_L, la norme de l'idéal J est égale au cardinal de l'anneau quotient O_L / J.

Le cas particulier des entiers quadratiques, plus simple, est étudié dans l'article Idéal de l'anneau des entiers d'un corps quadratique. Toujours si K est égal à Q la propriété de multiplicativité est conservé :

• Soit J₁ et J₂ deux idéaux de O_L, l'égalité suivante est vérifiée :

La démonstration se fonde sur le fait que l'anneau O_L est de Dedekind. Tout idéal est produit d'idéaux premiers et tout idéal premier est maximal. Il suffit de démontrer que la propriété est vraie pour les idéaux maximaux et multiplier par les facteurs premiers de J₂.

Enfin :

• Soit f un morphisme bijectif de Z module de O_L vers un idéal J, la norme relative de J est égale à la valeur absolue du déterminant de f.

Détails des démonstrations

• La valeur absolue de la norme relative d'un entier algébrique α de L sur Q est égal à l'ordre de l'anneau quotient O_L/ α.O_L :

Réseau de l'idéal principal du point 2 + i dans l'anneau des entiers de Gauss.

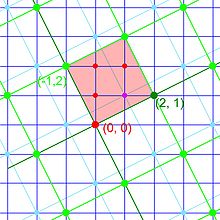
Soit B = (b₁, ..., b_d) une base de O_L et donc de L. La famille α.B égale à (α.b₁, ..., α.b_d) est aussi une base de L en tant que Q espace vectoriel et une base de α.O_L comme Z module. Tout élément γ de O_L s'exprime comme combinaison linéaire de la famille α.B à coefficients dans Q, γ est élément de α.O_L si et seulement si les coefficients sont des entiers relatifs. Soit F l'ensemble des points de L dont les coordonnées dans la base α.B sont éléments de l'intervalle [0,1[.

Cette configuration est illustrée sur la figure de droite, correspondant à l'anneau des entiers de Gauss et à α = 2 + i. Les points de l'anneau correspondent aux intersections du quadrillage, les point de l'idéal sont en verts et F est la surface illustrée en rouge.

Montrons que chaque classe de O_L/ α.O_L contient un unique représentant dans F :

Soit γ un représentant d'une classe de O_L/ α.O_L. Soit (c_i) ses coordonnées dans la base de L α.B. Sur la figure, la classe est représenté par les points bleus, le point γ peut, par exemple être choisi égal à 3 + 2.i.

Décomposons c_i en la somme de sa partie entière p_i et d'un reste r_i éléments de [0, 1[. Les éléments de O_L π et ρ sont définis par :

La famille (p_i) est composée d'entiers relatifs et α est élément de α.O_L, la famille (r_i) est composée d'éléments de l'intervalle [0,1[ et ρ est élément de F et de O_L car ρ = γ - π. La classe de γ possède un représentant ρ dans F. L'unicité résulte du fait que la différence des coordonnées de deux éléments de F dans la base α.B ne peut être entière. Sur la figure, le point ρ est égal à 1 + i, il correspond bien à l'un des 5 points de l'intersection de l'anneau et de F, en rouge sur la figure.

Montrons que F contient exactement N_K/Q(α) éléments dans O_L :

Le raisonnement utilisé est géométrique, il est de même nature que celui du théorème de Minkowski sur le nombre de points entiers dans un convexe symétrique par rapport à l'origine.

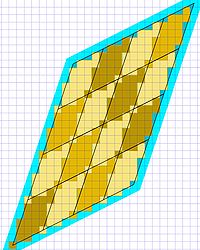
Soit m un entier naturel strictement positif et V le volume de K constitué par les vecteurs de coordonnées en valeur absolue inférieures à m dans la base α.B. On remarque de les translations de F par des vecteurs de coordonnées entières strictement inférieurs à m - 1, en valeur absolue, dans la base α.B forment une partition de V. La démonstration précédente montre de plus que chaque translaté contient exactement autant de points de O_L que F. Si V_p et F_p désignent le nombre de points de O_L dans V et F, l'égalité suivante est vérifiée :

La deuxième forme est la conséquence du résultat démontrée précédemment, le signe de la valeur absolue est utilisé ici pour désigner le cardinal de l'ensemble. Cette situation est illustrée en dimension 2 par les figures à droite et à gauche. La figure de gauche représente F, les points de l'intersection de F et de l'idéal sont au centre d'un carré jaune, le volume F est à l'intérieur de la frontière, en noir. La figure de droite représente V, ce volume est constitué de 16 volumes égaux à F ou à un translaté de F. L'égalité précédente exprime le fait qu'il existe exactement autant de petits carrés jaunes dans chaque volume translaté, autrement dit, ces petits carrés s'emboitent parfaitement.

Il existe une autre manière d'évaluer V_p, il consiste à établir le volume V_v de V. On munis l'espace d'un produit scalaire conférant à B le statut de base orthonormale. Considérons un pavage de l'espace par des cubes de côtés de longueur 1, dont les arêtes sont parallèles à un vecteur de la base B et dont le centre est un point de O_L. Ils correspondent aux carrés jaunes des deux figures. Soit V_v-1 le volume constitué par l'ensemble des cubes strictement inclus dans V et V_v+1 celui constitué par l'ensemble des cubes ayant une intersection non vide avec V. On obtient les majorations suivante :

Si S est la surface frontière du volume V et S_v sa mesure, on obtient :

.

Soit M un majorant de la mesure de la plus grande face du volume fondamental F, comme il existe 2.d faces et que chaque face du volume V est composée de (2m+ 1)^d-1 faces de F, on obtient les majorations suivantes :

.

Enfin V_v est l'image d'un volume de mesure égale à (2μ + 1)^d par une application linéaire de déterminant N_L/Q(α). En utilisant la valeur de V_p calculée précédemment, on obtient :

.

En simplifiant par (2m + 1)^d les majorations :

.

Si m est choisi plus grand que d.M, le fait que la norme relative de α et le cardinal du quotient soit des entiers naturels permet de conclure.

• Soit f un morphisme bijectif de Z module de O_L vers un idéal J, la norme relative de J est égale à la valeur absolue du déterminant de f.

Remarquons tout d'abord qu'un tel morphisme existe toujours. Le module O_L est noethérien car l'anneau associé est de Dedekind. Un idéal est un sous-module de même dimension que le corps, il admet une base. Toute application ayant bijective de B une base de J se prolonge en un morphisme de Z module bijectif.

Le raisonnement précédent s'applique encore. Il suffit de considérer comme volume fondamental l'ensemble des vecteurs de coordonnées élément de [0, 1[ dans la base image de B par f.

• Soient J₁ et J₂ deux idéaux de O_L, l'égalité suivante est vérifiée :

L'idéal J₂ est un produit d'idéaux maximaux (cf idéal fractionnaire). Il suffit donc de démontrer la proposition si J₂ est maximal, le cas général se traitant alors par multiplication successives d'idéaux maximaux.

Considérons la structure O_L / J₁.J₂. Elle peut être considérée comme le quotient d'un groupe additif par un sous-groupe. Il existe un morphisme de groupe canonique φ entre cette structure et O_L / J₁. En effet, si deux éléments de O_L diffèrent par un élément de J₁.J₂, ils diffèrent d'un élément de J₁ et ont même image dans O_L / J₁ et ce morphisme est surjectif. La théorie des groupes montre que si |Ker φ| désigne l'ordre du groupe noyau de φ :

.

Le noyau de φ est composé des éléments des classes des éléments de J₁ dans O_L / J₁.J₂, c'est-à-dire J₁ / J₁.J₂. On va montrer que ce noyau peut être vu comme un espace vectoriel de dimension 1 sur le corps O_L / J₂. Comme J₂ est un idéal maximal, ce quotient est bien un corps. Remarquons qu'il opère bien sur J₁ / J₁.J₂, soient deux éléments de O_L dont la différence est un élément de J₂, les produits de ces deux éléments par un membre de J₁ diffèrent par un élément de J₁.J₂, ce qui signifie que leur classe est bien la même dans J₁ / J₁.J₂. La structure J₁ / J₁.J₂ est bien celle d'un groupe abélien sur lequel opère un corps. Cette structure est celle d'un espace vectoriel.

Il reste encore à montrer que cet espace est de dimension 1. Soit α un élément de J₁ qui n'est pas dans J₁.J₂. (Un tel élément existe car sinon J₁ serait égal à J₁.J₂ et cet idéal disposerait de deux décompositions en idéaux premiers, ce qui est impossible.) Alors J₁^-1α est un idéal de O_L qui n'est pas inclus dans J₂, si bien que l'idéal J₁^-1α+J₂ contient strictement l'idéal maximal J₂, donc est égal à O_L. Ainsi, αO_L+J₁J₂=J₁, donc J₁ / J₁J₂ est isomorphe à αO_L / J₁J₂ qui, en tant qu'espace vectoriel, est de dimension 1, car engendré par la classe de α. Le cardinal de l'espace vectoriel est égal à celui de son corps ou encore à celui de la norme de J₂. Autrement dit, le noyau de φ est de cardinal la norme de J₂, ce qui termine la démonstration.

Applications

Les normes permettent parfois d'établir le caractère euclidien de certains anneaux d'entiers. Tel est le cas pour les entiers de Gauss, d'Eisenstein et les entiers de Q(√5).

Dans le cas plus général des corps quadratiques la norme aide à élucider la structure de l'anneau pour permettre par exemple de résoudre l'équation x² + 5.y² = n où n est un entier.

D'une manière encore plus générale, la norme est utilisée pour établir les résultats clé de la théorie algébrique des nombres, comme la structure des idéaux fractionnaires ou celle du groupe des classes d'idéaux.

Références

• Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
• Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]

Lien externe

Bas Edixhoven (de) et Laurent Moret-Bailly, Théorie algébrique des nombres, cours de maîtrise de mathématiques, université de Rennes 1, 2004 [lire en ligne] 

• Portail des mathématiques