Nombres décimaux
- Nombres décimaux
-
Nombre décimal
Un nombre décimal est un nombre possédant un développement décimal limité et pouvant s'écrire sous la forme 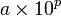 (où a et p sont des entiers relatifs). Ce n'est pas le cas, par exemple, du nombre
(où a et p sont des entiers relatifs). Ce n'est pas le cas, par exemple, du nombre 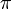 qui possède cependant autant d'approximations décimales que l'on veut :
qui possède cependant autant d'approximations décimales que l'on veut : 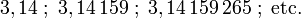
Caractérisation
Si a est un nombre rationnel, les propriétés suivantes sont équivalentes et caractérisent le fait que le nombre a est décimal :
- a admet un développement décimal limité (c'est-à-dire avec un nombre fini de chiffres différents de 0).
- Il existe
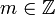 et
et 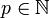 tels que :
tels que : 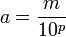 .
.
- La fraction irréductible de a est de la forme
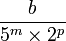 , où b est un entier relatif et m et p des entiers naturels.
, où b est un entier relatif et m et p des entiers naturels.
- a possède deux développements décimaux distincts.
Remarques
- La première assertion prouve que 1,6666 est un nombre décimal et que 1,6666... (qui s'écrirait avec une infinité de 6) n'en est pas un.
- La deuxième assertion nous dit que
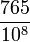 est un nombre décimal, mais elle ne peut pas être utilisée pour prouver qu'un nombre n'est pas décimal.
est un nombre décimal, mais elle ne peut pas être utilisée pour prouver qu'un nombre n'est pas décimal.
- La troisième assertion nous donne une méthode pour reconnaître si un nombre rationnel est décimal : il suffit de déterminer sa fraction irréductible (par exemple en calculant le PGCD de son numérateur et de son dénominateur), puis de tester si le dénominateur est uniquement divisible par 2 et 5.
- La quatrième assertion fait souvent figure de « curiosité ». Le nombre 2,5 peut aussi être écrit 2,4999... (avec une infinité de 9). Pour des détails, voir l'article Développement décimal de l'unité.
Structure algébrique
L'ensemble des décimaux est souvent noté 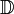 .
. 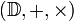 est un anneau intègre commutatif. Son corps des fractions étant
est un anneau intègre commutatif. Son corps des fractions étant  .
.
Topologie
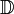 est dense dans
est dense dans  . Autrement dit, tout nombre réel est la limite d'une suite de nombres décimaux. Ce théorème est fréquemment utilisé lors de la recherche de valeurs approchées.
. Autrement dit, tout nombre réel est la limite d'une suite de nombres décimaux. Ce théorème est fréquemment utilisé lors de la recherche de valeurs approchées.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Type de nombre
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Nombres décimaux de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Nombres réels — Nombre réel Les nombres réels (dont l ensemble est noté ℝ) peuvent très informellement être conçus en mathématiques comme tous les nombres associés à des longueurs ou des grandeurs physiques. Ce sont les nombres, qu ils soient positifs, négatifs… … Wikipédia en Français
Décimaux — Nombre décimal Ne doit pas être confondu avec Base décimale. Un nombre décimal est un nombre possédant un développement décimal limité et pouvant s écrire sous la forme (où a et p sont des entiers relatifs). Ce n est pas le cas, par exemple … Wikipédia en Français
Nombres p-adiques — Nombre p adique En théorie des nombres, si p est un nombre premier, un nombre p adique est un objet mathématique qui peut se concevoir comme une suite de chiffres en base p, éventuellement infinie à gauche de la virgule (mais toujours finie à… … Wikipédia en Français
Nombres 600 a 699 — Nombres 600 à 699 Cet article recense les nombres qui ont des propriétés remarquables allant de 600 à 699. Sommaire 1 Entiers de 600 à 609 2 Entiers de 610 à 619 3 Entiers de 620 à 629 4 Enti … Wikipédia en Français
Nombres 600 À 699 — Cet article recense les nombres qui ont des propriétés remarquables allant de 600 à 699. Sommaire 1 Entiers de 600 à 609 2 Entiers de 610 à 619 3 Entiers de 620 à 629 4 Enti … Wikipédia en Français
Nombres premiers — Nombre premier 7 est un nombre premier car il admet exactement deux diviseurs positifs … Wikipédia en Français
Nombres 600 à 699 — Cet article recense les nombres qui ont des propriétés remarquables allant de 600 à 699. Sommaire 1 Entiers de 600 à 609 2 Entiers de 610 à 619 3 Entiers de 620 à 629 4 Entiers de 630 à … Wikipédia en Français
RÉELS (NOMBRES) — Par les différents adjectifs généralement accolés au substantif commun qu’est le nombre, la langue mathématique familière surprend et inquiète, car elle risque de susciter des confusions: nombres rationnels (d’autres nombres seraient donc sans… … Encyclopédie Universelle
Construction des nombres réels — En mathématiques, il existe différentes constructions des nombres réels, dont les deux plus connues sont les coupures de Dedekind, les suites de Cauchy. Sommaire 1 Construction intuitive à partir des nombres décimaux 2 Construction par les… … Wikipédia en Français
Construction Des Nombres Réels — Il existe différentes constructions des nombres réels, dont les deux plus rigoureuses sont les coupures de Dedekind, les suites de Cauchy. Sommaire 1 Construction intuitive à partir des nombres décimaux 2 Construction par les coupures de Dedekind … Wikipédia en Français
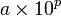 (où a et p sont des entiers relatifs). Ce n'est pas le cas, par exemple, du nombre
(où a et p sont des entiers relatifs). Ce n'est pas le cas, par exemple, du nombre 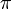 qui possède cependant autant d'approximations décimales que l'on veut :
qui possède cependant autant d'approximations décimales que l'on veut : 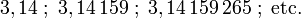
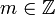 et
et 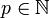 tels que :
tels que : 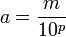 .
.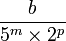 , où b est un entier relatif et m et p des entiers naturels.
, où b est un entier relatif et m et p des entiers naturels.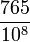 est un nombre décimal, mais elle ne peut pas être utilisée pour prouver qu'un nombre n'est pas décimal.
est un nombre décimal, mais elle ne peut pas être utilisée pour prouver qu'un nombre n'est pas décimal.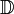 .
. 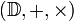 est un anneau intègre commutatif. Son corps des fractions étant
est un anneau intègre commutatif. Son corps des fractions étant  .
. est dense dans
est dense dans  . Autrement dit, tout nombre réel est la limite d'une suite de nombres décimaux. Ce théorème est fréquemment utilisé lors de la recherche de valeurs approchées.
. Autrement dit, tout nombre réel est la limite d'une suite de nombres décimaux. Ce théorème est fréquemment utilisé lors de la recherche de valeurs approchées.


 Nombre décimal •
Nombre décimal •