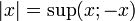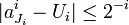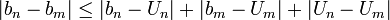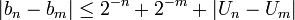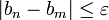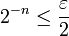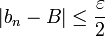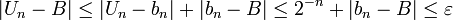- Construction Des Nombres Réels
-
Construction des nombres réels
Il existe différentes constructions des nombres réels, dont les deux plus rigoureuses sont
Sommaire
Construction intuitive à partir des nombres décimaux
Article détaillé : Développement décimal.Un nombre réel est une quantité qui a pour représentation décimale x = n + 0.d1d2d3..., où n est un entier, chaque di est un chiffre entre 0 et 9, et la séquence ne se termine pas par une infinité de 9. La définition de x est alors le nombre qui satisfait cette double inéquation pour tout k :
Construction par les coupures de Dedekind
Mise en place
C'est la construction imaginée par Richard Dedekind qui remarque que tout rationnel r coupe
 en deux ensembles : l'ensemble Ar des rationnels a tels a < r et l'ensemble Br des rationnels b tels
en deux ensembles : l'ensemble Ar des rationnels a tels a < r et l'ensemble Br des rationnels b tels 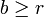 . Il appelle alors (Ar;Br) une coupure de
. Il appelle alors (Ar;Br) une coupure de  . Il remarque ensuite que
. Il remarque ensuite que 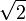 peut aussi partager
peut aussi partager  en deux ensembles : l'ensemble A des rationnels a tels que
en deux ensembles : l'ensemble A des rationnels a tels que 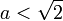 et l'ensemble B des rationnels b tels que
et l'ensemble B des rationnels b tels que 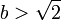 . L'idée lui vient donc de définir l'ensemble des réels comme l'ensemble des coupures de
. L'idée lui vient donc de définir l'ensemble des réels comme l'ensemble des coupures de  . Reste maintenant à définir une coupure sans se servir de la notion intuitive de nombre réel. Dedekind propose la définition suivante :
. Reste maintenant à définir une coupure sans se servir de la notion intuitive de nombre réel. Dedekind propose la définition suivante :- Une coupure de Dedekind dans le corps
 des rationnels est un couple de 2 sous-ensembles non-vides A et B tels que
des rationnels est un couple de 2 sous-ensembles non-vides A et B tels que
On voit ainsi que tout nombre rationnel r définit deux coupures :
- (A, B) telle que A est l'ensemble des rationnels strictement inférieurs à r et B l'ensemble des rationnels supérieurs ou égaux à r
- (A', B') telle que A' est l'ensemble des rationnels inférieurs ou égaux à r et B' l'ensemble des rationnels strictement supérieurs à r.
Pour lever cette ambiguïté, on utilise alors la définition suivante d'une coupure :
- Une coupure de
 est une partie A de
est une partie A de  telle que
telle que
- A est non vide et différente de

- pour tout a de A, si a' < a alors a' appartient à A
- A ne possède pas de plus grand élément.
- A est non vide et différente de
On définit alors
 comme l'ensemble de ces coupures. On peut remarquer que cette seconde définition permet d'assurer une correspondance univoque entre chaque rationnel r et la coupure Ar définie comme l'ensemble de tous les rationnels a tels que a < r. On remarque alors que
comme l'ensemble de ces coupures. On peut remarquer que cette seconde définition permet d'assurer une correspondance univoque entre chaque rationnel r et la coupure Ar définie comme l'ensemble de tous les rationnels a tels que a < r. On remarque alors que  se divise en deux ensembles, l'un comprenant les coupures dont le complémentaire admet un plus petit élément, coupure de la forme Ar, et l'autre comprenant les coupures dont le complémentaire ne possède pas de plus petit élément.
se divise en deux ensembles, l'un comprenant les coupures dont le complémentaire admet un plus petit élément, coupure de la forme Ar, et l'autre comprenant les coupures dont le complémentaire ne possède pas de plus petit élément.Par exemple l'irrationnel
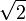 est représenté par la coupure
est représenté par la coupure 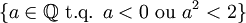 .
.On plonge naturellement
 dans
dans  par l'application injective qui, à tout rationnel r associe la coupure Ar
par l'application injective qui, à tout rationnel r associe la coupure ArPropriétés
Relation d'ordre : L'ensemble des coupures, muni de la relation d'inclusion est alors un ensemble totalement ordonné vérifiant de plus la propriété de la borne supérieure (tout ensemble non vide majoré possède une borne supérieure).
Addition : On peut alors construire une addition sur
 de la manière suivante :
de la manière suivante :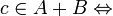 il existe a dans A et b dans B tels que c = a + b.
il existe a dans A et b dans B tels que c = a + b.
Cette addition confère à
 une structure de groupe commutatif. La seule difficulté consiste en la définition de l'opposé de A : A − r (si A = Ar) ou
une structure de groupe commutatif. La seule difficulté consiste en la définition de l'opposé de A : A − r (si A = Ar) ou 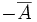 (si
(si  )
)Multiplication : La construction de la multiplication est plus subtile. Elle est définie sur tous les réels positifs de la manière suivante:
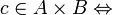 il existe a dans
il existe a dans 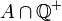 et b dans
et b dans 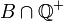 tels que
tels que 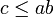 .
.
La règle des signes permettant alors de construire la multiplication sur tout

L'ensemble
 muni des ces deux lois est alors un corps commutatif archimédien complet.
muni des ces deux lois est alors un corps commutatif archimédien complet.Construction via les suites de Cauchy
Cette construction est plus difficile à aborder mais elle offre deux avantages : la construction des opérations y est plus naturelle et elle a le mérite de se généraliser à tout espace métrique.
Définition en tant qu'ensemble
L'idée de Cantor (et quelques années avant lui de Méray) réside dans le fait que l'on peut atteindre tout nombre réel par une suite de Cauchy de nombres rationnels. C’est-à-dire une suite (un) vérifiant le critère de convergence suivant :
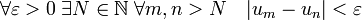
L'élément limite auquel il va falloir donner un sens sera alors défini comme un nombre réel. L'ensemble des suites de Cauchy sur
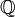 , que nous notons
, que nous notons 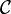 , apparaît cependant bien trop vaste. En effet, par exemple pour un rationnel donné, il existe une infinité de suites de Cauchy convergeant vers cette limite. Il est nécessaire de quotienter cet espace par une relation d'équivalence entre les suites. Si nous notons
, apparaît cependant bien trop vaste. En effet, par exemple pour un rationnel donné, il existe une infinité de suites de Cauchy convergeant vers cette limite. Il est nécessaire de quotienter cet espace par une relation d'équivalence entre les suites. Si nous notons  cette relation d'équivalence entre deux suites (un) et (vn), elle est définie de la manière suivante :
cette relation d'équivalence entre deux suites (un) et (vn), elle est définie de la manière suivante :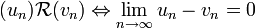
Nous pouvons remarquer que la relation
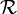 est bien réflexive car la suite nulle converge bien vers 0, symétrique car si une suite converge vers 0, alors la suite opposée converge aussi vers 0, et la transitivité est une conséquence de l'inégalité triangulaire sur la valeur absolue dans
est bien réflexive car la suite nulle converge bien vers 0, symétrique car si une suite converge vers 0, alors la suite opposée converge aussi vers 0, et la transitivité est une conséquence de l'inégalité triangulaire sur la valeur absolue dans  . Si (un), (vn) et (wn) sont trois suites rationnels, nous avons en effet:
. Si (un), (vn) et (wn) sont trois suites rationnels, nous avons en effet: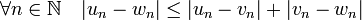
Toute relation d'équivalence sur un ensemble définit une partition de cet ensemble. Un élément de cette partition est appelé nombre réel, et l'ensemble des nombres réels est noté
 .
.Remarque : lorsque l'on fait tendre quelque chose vers une limite ici, c'est par des
 rationnels que l'on va encadrer, car on ne dispose pas encore des réels !
rationnels que l'on va encadrer, car on ne dispose pas encore des réels !Définition en tant que corps
L'ensemble des suites dans
 est naturellement muni d'une structure d'anneau avec l'addition et la multiplication héritées de la structure de corps dans
est naturellement muni d'une structure d'anneau avec l'addition et la multiplication héritées de la structure de corps dans  . Si (un) et (vn) sont deux suites, alors ces opérations sont définies par :
. Si (un) et (vn) sont deux suites, alors ces opérations sont définies par :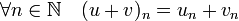
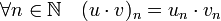
Ces opérations conservent le critère de Cauchy, ainsi la somme et le produit de deux suites de Cauchy sont encore des suites de Cauchy. Il est ainsi possible de munir
 d'une structure d'anneau.
d'une structure d'anneau.Ces opérations conservent la partition définie par la relation
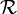 . Ainsi quel que soit les représentants choisis de deux classes de
. Ainsi quel que soit les représentants choisis de deux classes de 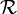 la somme (resp. la multiplication) des représentants appartient à la même classe de
la somme (resp. la multiplication) des représentants appartient à la même classe de 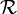 . Il est ainsi possible de munir
. Il est ainsi possible de munir  d'une structure d'anneau. On vérifie alors que la classe de (0) est l'élément neutre et la classe de (1) l'unité. On vérifie que
d'une structure d'anneau. On vérifie alors que la classe de (0) est l'élément neutre et la classe de (1) l'unité. On vérifie que  est de plus un corps commutatif.
est de plus un corps commutatif.On plonge
 dans
dans  via les suites stationnaires. On notera (a) la classe contenant la suite constante égale à
via les suites stationnaires. On notera (a) la classe contenant la suite constante égale à 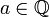 .Démonstrations
.DémonstrationsMontrons tout d'abord que (
 , + ) est un groupe abélien:
, + ) est un groupe abélien:- L'addition est commutative. En effet, soit a et b deux éléments de
 et (an) et (bn) deux suites rationnelles représentant de leurs classes. Alors par définition (an + bn) (resp. (bn + an)) est représentant de la classe a + b (resp. b + a). Or ces deux suites sont égales. Ce qui nous montre que a + b est égal à b + a.
et (an) et (bn) deux suites rationnelles représentant de leurs classes. Alors par définition (an + bn) (resp. (bn + an)) est représentant de la classe a + b (resp. b + a). Or ces deux suites sont égales. Ce qui nous montre que a + b est égal à b + a.
- L'addition est associative. En effet, un raisonnement de la même nature que le précédent nous montre sans difficulté l'associativité de
 .
.
- 0 est l'élément neutre de l'addition. Soit a un élément de
 et (an) une suite rationnelle de la classe de a. Notons 0 la suite constante égale à 0. Cette suite est par définition du plongement de
et (an) une suite rationnelle de la classe de a. Notons 0 la suite constante égale à 0. Cette suite est par définition du plongement de  dans
dans  dans la classe de 0. alors la suite (an + 0), est un élément de la classe de a + 0 et aussi un élément de la classe de a. On a démontré que a + 0 est égal à a.
dans la classe de 0. alors la suite (an + 0), est un élément de la classe de a + 0 et aussi un élément de la classe de a. On a démontré que a + 0 est égal à a.
- Tout nombre réel admet un opposé. Soit a un élément de
 et (an) une suite rationnelle de la classe de a. Notons -a le réel dont la classe contient la suite ( − an) qui par définition est rationnelle. Alors la suite (an − an) représentant de la classe de 0 est aussi un représentant de la classe a + (-a). On en déduit que a - a = 0.
et (an) une suite rationnelle de la classe de a. Notons -a le réel dont la classe contient la suite ( − an) qui par définition est rationnelle. Alors la suite (an − an) représentant de la classe de 0 est aussi un représentant de la classe a + (-a). On en déduit que a - a = 0.
Montrons ensuite que (
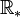 , . ) est un groupe abélien.
, . ) est un groupe abélien.- La multiplication est commutative. La démonstration est l'analogue de celle qui prouve la commutativité de l'addition.
- La multiplication est associative. La démonstration est l'analogue de celle qui prouve l'associativité de la multiplication.
- 1 est l'élément neutre de la multiplication. La démonstration est l'analogue de celle qui prouve l'associativité de la multiplication.
- Tout nombre réel différent de 0 admet un inverse. Soit a un élément de
 différent de 0 et
différent de 0 et 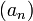 une suite rationnelle de la classe de a. Dire que a est différent de 0 c'est dire que la suite
une suite rationnelle de la classe de a. Dire que a est différent de 0 c'est dire que la suite 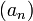 n'a pas pour limite 0. et donc:
n'a pas pour limite 0. et donc:
-
- Il y a donc une infinité de termes de la suite qui ont un module plus grand que l. Comme cette suite est de Cauchy, à partir d'un certain rang, le module de la différence de deux termes est plus petit que la moitié de l. On en déduit qu'à partir d'un certain rang, tous les termes de la suite sont différents de 0. Soit la suite
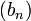 définie par
définie par  si
si  est différent de 0 et
est différent de 0 et 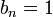 sinon. La suite
sinon. La suite 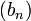 possède une section finissante égale à
possède une section finissante égale à 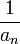 car la proposition (1) nous garantit que
car la proposition (1) nous garantit que 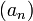 possède une section finissante dont toutes les valeurs sont strictement différente de 0. On en déduit que la suite
possède une section finissante dont toutes les valeurs sont strictement différente de 0. On en déduit que la suite 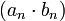 possède une section finissante égal à 1. on en déduit que a . b est égal à 1. Et tout nombre réel non nul admet bien un inverse.
possède une section finissante égal à 1. on en déduit que a . b est égal à 1. Et tout nombre réel non nul admet bien un inverse.
Montrons enfin que (
 , +, . ) est un corps.
, +, . ) est un corps.- La multiplication est distributive par rapport à l'addition. Cette démonstration termine la preuve de la propriété de corps de
 . Elle est analogue à celle qui prouve l'associativité de l'addition.
. Elle est analogue à celle qui prouve l'associativité de l'addition.
Relation d'ordre
On définit
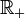 de la manière suivante :
de la manière suivante : 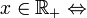
-
- x = 0
- ou
- il existe une suite de Cauchy rationnelle (an) et un rationnel positif r tel que (an) soit un représentant de x et an > r à partir d'un certain rang
et
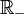 de la manière suivante :
de la manière suivante : 
-
- x = 0
- ou
- il existe une suite de Cauchy rationnelle (an) et un rationnel négatif r tel que (an) soit un représentant de x et an < r à partir d'un certain rang.
On définit alors une relation d'ordre sur
 en posant
en posantOn démontre que
 muni de cette relation d'ordre est un corps totalement ordonné archimédien et que cette relation d'ordre coïncide avec la relation d'ordre sur
muni de cette relation d'ordre est un corps totalement ordonné archimédien et que cette relation d'ordre coïncide avec la relation d'ordre sur  Démonstrations
Démonstrations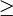 est une relation d'ordre.
est une relation d'ordre.
- Elle est réflexive : x − x = 0 donc
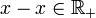 donc
donc 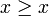 .
. - Elle est transitive. Il suffit de prouver que
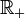 est stable par addition. Ensuite on pourra dire : si
est stable par addition. Ensuite on pourra dire : si 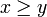 et si
et si 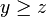 , alors
, alors 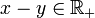 et
et 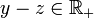 . Par addition
. Par addition 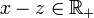 , donc
, donc 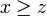 .
. - Elle est antisymétrique. Il suffit de prouver que
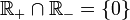 . Ensuite on pourra dire : si
. Ensuite on pourra dire : si 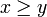 et si
et si 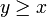 alors
alors 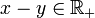 et
et 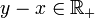 . Donc y − x = 0 donc x = y
. Donc y − x = 0 donc x = y
- L'ordre est total
- Il suffit de prouver que
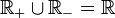 et que
et que 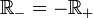 . Ensuite on pourra dire que , pour tous x et y, x − y appartient à
. Ensuite on pourra dire que , pour tous x et y, x − y appartient à 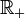 ou
ou 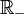 . Dans le dernier cas, on aura
. Dans le dernier cas, on aura 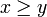 , dans le second cas, on aura y − x dans
, dans le second cas, on aura y − x dans 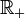 et
et 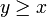 .
.
- L'ordre est compatible avec l'addition
- Pour tous x, y, z, si
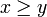 alors
alors 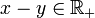 donc
donc 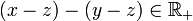 donc
donc 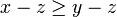 .
.
- L'ordre est compatible avec la multiplication par un réel positif
- Il suffit de montrer que
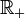 est stable par multiplication. Ensuite on pourra dire que , pour tous x, y, z, si
est stable par multiplication. Ensuite on pourra dire que , pour tous x, y, z, si 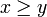 et si
et si 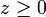 alors x − y et z appartiennent à
alors x − y et z appartiennent à 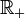 donc
donc  donc
donc 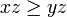 .
.
- La relation d'ordre coïncide avec la relation d'ordre sur

- Par définition de
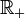 , cet ensemble contient tous les rationnels positifs.
, cet ensemble contient tous les rationnels positifs.
 est archimédien
est archimédien
- Il s'agit de montrer que, pour tous réel
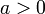 et
et 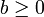 , il existe un entier
, il existe un entier 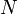 tel que
tel que 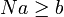 . Il suffit de poser
. Il suffit de poser 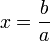 . Le réel x a pour représentant (xn) suite de Cauchy rationnelle donc majorée. On prend un majorant M entier de cette suite et on définit N par N = M + 1. Pour tout entier n, on a alors N − xn > 1 / 2 donc
. Le réel x a pour représentant (xn) suite de Cauchy rationnelle donc majorée. On prend un majorant M entier de cette suite et on définit N par N = M + 1. Pour tout entier n, on a alors N − xn > 1 / 2 donc 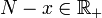 donc
donc 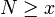 donc
donc 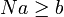 .
.
Distance et limite
La valeur absolue est alors définie par
On remarque alors que si (an) est un représentant de x alors ( | an | ) est un représentant de | x | .
On peut alors munir
 d'une distance
d'une distance- d(x , y)= |x - y|
et y définir la convergence de suite.
On démontre à ce propos que, si x a pour représentant la suite de Cauchy rationnelle (xn), alors cette suite est aussi une suite de réels (
 est plongé dans
est plongé dans  par la correspondance suivante : r a pour représentant la suite constante (r)) et cette suite de réels a pour limite x. Cela permet en autre de prouver que
par la correspondance suivante : r a pour représentant la suite constante (r)) et cette suite de réels a pour limite x. Cela permet en autre de prouver que  est dense dans
est dense dans  car tout réel est limite d'une suite de rationnels.
car tout réel est limite d'une suite de rationnels.On démontre aussi que, sur cet ensemble, la limite d'une somme est égale à la somme des limites, la limite d'un produit au produit des limites et que la limite d'une suite positive est positive ou nulle.
Complétude et borne supérieure
On sait déjà que, par construction, toutes les suites de Cauchy rationnelles convergent dans
 . Mais on démontre que c'est aussi le cas pour toute suite de Cauchy réelle.
. Mais on démontre que c'est aussi le cas pour toute suite de Cauchy réelle.Cette méthode de construction se généralise à tout espace métrique E pour obtenir un espace métrique complet E' tel que E soit dense dans E'.
On démontre de plus que
 vérifie la propriété de la borne supérieure : tout sous-ensemble non vide majoré possède une borne supérieure.Démonstrations
vérifie la propriété de la borne supérieure : tout sous-ensemble non vide majoré possède une borne supérieure.Démonstrations est complet La démonstration est un peu subtile. En effet dire que
est complet La démonstration est un peu subtile. En effet dire que  est complet, revient à dire que toute suite
est complet, revient à dire que toute suite  de Cauchy à valeur dans
de Cauchy à valeur dans  est convergente. On utilisera ici les majuscules pour désigner les réels et les minuscules pour désigner les rationnels. Chaque
est convergente. On utilisera ici les majuscules pour désigner les réels et les minuscules pour désigner les rationnels. Chaque 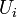 est représenté par une suite
est représenté par une suite  de rationnels. Nous avons donc affaire à une suite de suites. La démonstration s'inspire de la méthode de la diagonale de Cantor. Elle consiste à prendre des termes dans chaque suite
de rationnels. Nous avons donc affaire à une suite de suites. La démonstration s'inspire de la méthode de la diagonale de Cantor. Elle consiste à prendre des termes dans chaque suite  pour que cela fonctionne.
pour que cela fonctionne.
- Pour tout entier
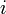 , la suite
, la suite  converge vers
converge vers 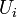 donc il existe
donc il existe  tel que
tel que
- On note alors
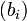 la suite de rationnels
la suite de rationnels 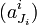
- Pour tout
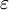 positif, il existe un entier
positif, il existe un entier 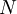 , tel que pour tous
, tel que pour tous 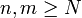 , on a
, on a
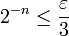
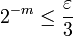
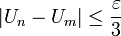 car
car 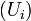 est une suite de Cauchy
est une suite de Cauchy
- Alors on pourra écrire :
- La suite de rationnels
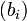 est alors une suite de Cauchy qui converge vers un réel
est alors une suite de Cauchy qui converge vers un réel 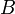
- Pour tout
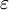 positif, il existe un entier
positif, il existe un entier 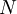 , tel que, pour tout
, tel que, pour tout 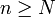 , on a
, on a
- Alors on pourra écrire:
- La suite de réels
 converge alors vers
converge alors vers 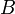
 satisfait à la propriété de la borne supérieure. Soit
satisfait à la propriété de la borne supérieure. Soit 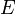 un ensemble non vide (contenant un réel
un ensemble non vide (contenant un réel  ) majoré par un réel
) majoré par un réel  . Si
. Si  est un majorant de
est un majorant de 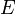 alors le problème est terminé car
alors le problème est terminé car  est le plus grand élément de
est le plus grand élément de 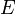 et donc sa borne supérieure. Sinon, on procède par dichotomie pour prouver que
et donc sa borne supérieure. Sinon, on procède par dichotomie pour prouver que 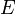 possède une borne supérieure (plus petit des majorants). On crée deux suites
possède une borne supérieure (plus petit des majorants). On crée deux suites 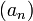 et
et  définies par récurrence de la manière suivante :
définies par récurrence de la manière suivante :
-
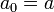 et
et 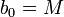
- pour tout entier
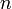 ,
,
- si
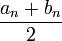 est un majorant ,
est un majorant ,  et
et 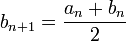
- si
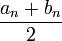 n'est pas un majorant ,
n'est pas un majorant ,  et
et 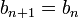
- si
- La suite
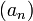 est alors une suite de réels dont aucun terme n'est un majorant de
est alors une suite de réels dont aucun terme n'est un majorant de 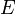 et la suite
et la suite  est une suite de réels dont tous les termes sont des majorants de
est une suite de réels dont tous les termes sont des majorants de 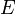 . Ensuite, le principe de construction assure que
. Ensuite, le principe de construction assure que 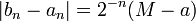 .
.
- ce qui nous assure que
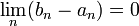
- Enfin, ce même principe de construction assure que, pour tout
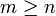 ,
,
- En particulier ,
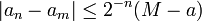 et
et 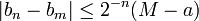 , ce qui permet de dire que les suites
, ce qui permet de dire que les suites 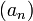 et
et  sont de Cauchy. Puisque
sont de Cauchy. Puisque  est complet, ces suites convergent et comme
est complet, ces suites convergent et comme 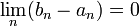 , elles convergent vers le même réel
, elles convergent vers le même réel 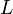 . Il reste à montrer que
. Il reste à montrer que 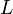 est bien la borne supérieure.
est bien la borne supérieure. - Pour tout réel
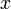 de
de 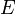 ,
, 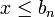 car
car 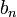 est un majorant. Donc par passage à la limite, pour tout réel
est un majorant. Donc par passage à la limite, pour tout réel 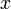 de
de 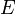 ,
, 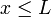 .
. 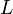 est donc bien un majorant de
est donc bien un majorant de 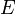 .
. - Pour tout réel
 majorant de
majorant de 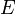 ,
,  car
car 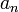 n'est jamais un majorant. Par passage à la limite, pour tout majorant
n'est jamais un majorant. Par passage à la limite, pour tout majorant  de
de 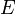 ,
, 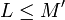 .
. 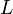 est bien le plus petit des majorants.
est bien le plus petit des majorants.
Liens externes
- Une construction de R par les coupures [pdf] par Jean Gounon
- Une construction de R par les suites de Cauchy [pdf]
- Portail des mathématiques
Catégories : Nombre | Théorie des ensembles | Construction classique
Wikimedia Foundation. 2010.