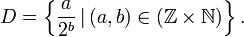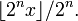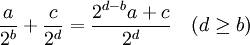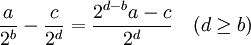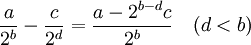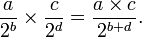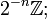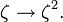Nombre dyadique

Nombre dyadique

Fraction dyadique

En mathématiques, une fraction dyadique ou rationnel dyadique est un nombre rationnel qui, lorsqu'il est écrit sous forme de fraction, possède un dénominateur sous forme de puissance de deux. On peut le noter formellement par

D=\left\{ \frac{a}{2^b}\,|\, (a,b) \in (\Z\times \N) \right\}.

Par exemple, 1/2 ou 3/8 sont des fractions dyadiques, mais pas 1/3. Ce sont précisément les nombres qui ont un développement de « décimales » binaire fini.

Le pouce est habituellement divisé de manière dyadique plutôt qu'en fractions décimales; de manière similaire, les divisions habituelles du gallon en demi--gallons, quarts et pintes sont dyadiques. Les anciens égyptiens utilisaient aussi les fractions dyadiques dans les mesures, avec des dénominateurs allant jusqu'à 64.

L'ensemble de toutes les fractions dyadiques est dense dans l'ensemble des nombres réels; un nombre réel quelconque x peut être arbitrairement approché autant que l'on veut par des rationnels dyadiques de la forme

\lfloor 2^n x \rfloor / 2^n.

Comparé aux autres sous-ensembles de la droite réelle, tels que les nombres rationnels, c'est un ensemble dense dans un certain sens, plutôt « petit », c'est pourquoi il apparaît quelquefois dans les démonstrations de topologie comme le lemme d'Urysohn.

La somme, le produit ou la différence de deux fractions dyadiques quelconque est elle-même une autre fraction dyadique :

\frac{a}{2^b}+\frac{c}{2^d}=\frac{2^{d-b}a+c}{2^d} \quad (d\ge b)
\frac{a}{2^b}-\frac{c}{2^d}=\frac{2^{d-b}a-c}{2^d} \quad (d\ge b)
\frac{a}{2^b}-\frac{c}{2^d}=\frac{a-2^{b-d}c}{2^b} \quad (d< b)
\frac{a}{2^b}\times \frac{c}{2^d} = \frac{ a \times c}{2^{b+d}}.

Par contre, le résultat de la division d'une fraction dyadique par une autre n'est pas, en général, une fraction dyadique. Ainsi, les fractions dyadiques forment un sous-anneau de l'ensemble des nombres rationnels 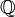\mathbb{Q}\,. Algébriquement, ce sous-anneau est la localisation des entiers 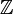\mathbb{Z}\, qui respecte l'ensemble des puissances de deux.

Les nombres surréels sont générés par un principe de construction itérative qui commence en générant toutes les fractions dyadiques finies, puis conduit à la création de nouvelles et étranges sortes de nombres infinis, infinitésimaux et autres.

Solénoïde dyadique

Article détaillé : Solénoïde (mathématiques).

En tant que groupe abélien additif, l'ensemble des rationnels dyadiques est la limite directe des sous-groupes cycliques infinis

2^{-n}\mathbb{Z};

pour n = 0, 1, 2, ... . Dans l'esprit de la dualité Pontryagin, il existe un objet dual, nommément la limite inverse du groupe du cercle unité sous l'application carrée répétée

\zeta \rightarrow \zeta^2.

Le groupe topologique résultant D est appelé le solénoïde dyadique.

Un élément du solénoïde dyadique peut être représenté comme une suite infinie de nombres complexes :

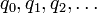q_0, q_1, q_2, \ldots\,, avec la propriété que chaque qi se place sur le cercle unité et que, pour tous les i > 0,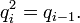
q_i^2 = q_{i-1}.

L'opération de groupe sur ces éléments multiplie deux suites quelconques convenablement.

En tant qu'espace topologique, c'est un continuum indécomposable.

Voir aussi

Notion de nombre
Ensembles usuels \mathbb{N} Entier naturel • \mathbb{Z} Entier relatif • \mathbb{D} Nombre décimal • \mathbb{Q} Nombre rationnel • \mathbb{R} Nombre réel • \mathbb{C} Nombre complexe Mathématiques
Extensions \mathbb{H} Quaternion • \mathbb{O} Octonion • \mathbb{S} Sédénion • Nombre complexe fendu • Tessarine • Nombre bicomplexe • Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • \mathbb{Q}_p Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • i Unité imaginaire • e Constante de Neper • ℵ0 Aleph-zéro • Table de constantes mathématiques
Notions connexes Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fraction dyadique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre dyadique de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • dyadique — [ djadik ] adj. • 1701; de dyade ♦ Qui concerne une dyade. ⇒ binaire. Relation dyadique. Math. Nombre dyadique : nombre rationnel de la forme (a/2)k, où a est un rationnel et k un entier naturel. ● dyadique adjectif …   Encyclopédie Universelle

  • Nombre rationnel dyadique — ● Nombre rationnel dyadique rationnel r tel qu il existe un entier naturel m pour lequel le produit 2mr est un entier …   Encyclopédie Universelle

  • Nombre D'or —  Pour l’article homonyme, voir Nombre d or (astronomie).  La proportion définie par a et b est dite d extrême et de moyenne raison lorsque a e …   Wikipédia en Français

  • Nombre Parfait — Un nombre parfait est un nombre entier n strictement supérieur à 1 qui est égal à la somme de ses diviseurs stricts, autrement dit, tel que où σ(n) est la somme des diviseurs entiers positifs de n, n non compris. Le premier nombre parfait est 6,… …   Wikipédia en Français

  • Nombre Premier — 7 est un nombre premier car il admet exactement deux diviseurs positifs …   Wikipédia en Français

  • Nombre d'Or —  Pour l’article homonyme, voir Nombre d or (astronomie).  La proportion définie par a et b est dite d extrême et de moyenne raison lorsque a e …   Wikipédia en Français

  • Nombre d’or — Nombre d or  Pour l’article homonyme, voir Nombre d or (astronomie).  La proportion définie par a et b est dite d extrême et de moyenne raison lorsque a e …   Wikipédia en Français

  • Nombre+transcendant — Nombre transcendant En mathématiques, un nombre transcendant est un nombre réel ou complexe qui n est racine d aucune équation polynomiale : où et les coefficients sont des nombres entiers (donc des rationnels), dont au moins l un an est non …   Wikipédia en Français

  • Nombre Algébrique — Un nombre algébrique, en mathématiques, est tout nombre qui est solution d une équation algébrique (autrement dit racine d un polynôme différent de zéro) à coefficients entiers (ou de manière équivalente, à coefficients rationnels). Sans plus de… …   Wikipédia en Français

  • Nombre Cardinal — Pour les articles homonymes, voir Cardinal. En mathématiques, la cardinalité est une notion de taille pour les ensembles. Les nombres cardinaux permettent donc de mesurer l ampleur de tout ensemble, même infini, là où les entiers naturels ne… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”