Lemme d'Urysohn

Le lemme d'Urysohn est un résultat de topologie, qui établit que pour deux fermés disjoints A et B d'un espace normal X (ou plus généralement d'un espace T₄), il existe une fonction continue de X dans l'intervalle [0, 1] qui vaut 1 sur A et 0 sur B. On le considère parfois comme le « premier résultat non trivial sur les espaces topologiques ».^{[réf. souhaitée]}

Ce lemme permit d'étendre aux espaces normaux le théorème de prolongement de Tietze, initialement démontré en 1914 par Heinrich Tietze pour les espaces métriques^[1]. Pavel Urysohn trouve une nouvelle démonstration et énonce son lemme un peu plus tard, dans un texte mathématique dont l'objectif est la démonstration des théorèmes sur l'invariance de la dimension d'un espace topologique localement homéomorphe à un espace euclidien.

Sommaire 1 Énoncés 2 Approche qualitative 2.1 Fragment d'histoire 2.2 Démonstration intuitive 2.3 Usages 3 Démonstrations topologiques 3.1 Lemme d'Urysohn 3.2 Corollaire 4 Démonstrations différentielles 4.1 Fonction plateau 4.2 Lemme 5 Notes et références 6 Voir aussi 6.1 Bibliographie 7 Lien externe

Énoncés

Il existe un premier énoncé spécifique aux espaces T₄ (et dont la réciproque est immédiate) :

Un premier corollaire est que tout espace normal (i.e. T₄ et séparé) est complètement régulier.

Un autre corollaire est le suivant^[2] :

• Si X est un espace localement compact alors, pour tout compact K de X, il existe une application continue de X dans [0, 1], à support compact, et qui vaut 1 sur K.

Ce lemme est aussi utilisé en géométrie différentielle sous la forme suivante^[3] :

• Soient K un compact d'un espace euclidien E et Ω un ouvert de E contenant K. Il existe une fonction infiniment différentiable de E dans [0, 1], dont le support est inclus dans Ω, et qui vaut 1 sur K.

Approche qualitative

Fragment d'histoire

Une des grandes questions qui se posent au début du XX^e siècle en topologie est la classification des différents espaces. Un invariant important pour ce classement est la dimension. Si un espace topologique connexe possède en tout point un ouvert, contenant ce point et homéomorphe à un ouvert d'un espace euclidien, tous les espaces euclidiens ont la même dimension et cette dimension est unique^[4]. Si ce résultat est très intuitif : si un espace topologique est de même nature qu'une courbe, ce n'est alors pas un plan, la démonstration est difficile. Depuis Peano, la connaissance d'une fonction continue et surjective de R dans [0, 1]² illustre un des écueils à éviter, pour trouver des démonstrations rigoureuses.

Heinrich Tietze travaille sur cette question et, dans ce contexte, montre en 1914 que si f est une application continue définie sur un fermé d'un espace métrique, elle est continument prolongeable sur l'espace entier^[5]. Il trouve la définition d'espace normal en 1923^[6]. Pavel Urysohn, un mathématicien russe, parvient à démontrer le théorème clé de la dimension qu'il publie^[7] en 1924. Il retrouve des résultats déjà démontrés par Luitzen Brouwer en 1912, mais qu'Urysohn ne connaissait pas^[8]. Cette publication contient le lemme de l'article.

On doit encore à Tietze aussi le théorème de prolongement, qui porte maintenant son nom et dont le lemme de l'article n'est qu'un cas particulier^[8]. Jean Dieudonné développe l'usage du théorème en géométrie différentielle et développe simultanément et indépendamment avec Salomon Bochner la notion de partition de l'unité^[9] en 1937. Il introduit aussi la définition d'espace paracompact^[9] en 1944, elle remplace souvent celle d'espace normal, qui contient trop d'exceptions pathologiques pour être véritablement fertile en topologie algébrique^[6].

Démonstration intuitive

Intuitivement, il n'est pas très difficile d'imaginer une démonstration, se fondant sur la notion d'oscillation d'une fonction. L'oscillation d'une fonction f, définie sur un espace topologique et à valeurs dans un espace métrique, en un point x, est la borne inférieure des diamètres des images des voisinages de x. Si l'oscillation est nulle, la fonction est continue.

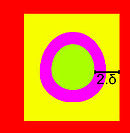
On suppose que les deux fermés A et B sont illustrés en rouge et vert sur la figure de droite. On peut définir une fonction f₁ qui vaut 1 sur A, 0 sur B et 1/2 partout ailleurs. Cette fonction est illustrée sur le graphique numéroté 1 (le jaune est la couleur milieu entre le rouge et le vert). L'axiome définissant un espace topologique normal montre qu'il existe un ouvert A₁₁ contenant A et tel que son adhérence soit strictement incluse dans le complémentaire de B, car le complémentaire de B est un ouvert contenant A. Il est alors possible de définir la fonction f₂ comme valant 1 sur A, 0 sur B 1/2 sur la frontière de A₁₁, 3/4 sur le complémentaire de A dans A₁₁ et 1/4 ailleurs. Cette fonction est représentée dans l'illustration numérotée 2. Cette fois-ci, l'oscillation de la fonction ne dépasse pas 1/4.

En réitérant la démarche, on obtient une fonction f₃ dont l'oscillation ne dépasse pas 1/8 puis une fonction (numéroté 3). En prolongeant la démarche, on obtient une fonction f_n dont l'oscillation ne dépasse pas 2 ^-n. Les fonctions deviennent de plus en plus continues, même si aucune ne l'est vraiment. Graphiquement, cela se traduit par le fait que le dégradé de couleur entre A et B est de plus en plus lisse.

La suite (f_n) converge uniformément, elle admet donc une limite f car l'intervalle [0, 1] est complet. Cette limite devrait satisfaire les hypothèses du lemme^[10].

Usages

On trouve le lemme d'Urysohn dans deux contextes géométriques différents.

• En topologie algébrique, ce lemme est utilisé pour établir des résultats topologiques fondamentaux. Ainsi l'une des démonstrations du théorème de Jordan, qui indique qu'un lacet sépare l'espace en deux composantes connexes, utilise le théorème de prolongement de Tietze, lequel — malgré l'existence d'une démonstration directe plus simple^[11] — se déduit, par tradition, du lemme d'Urysohn.

• En géométrie différentielle, le lemme d'Urysohn est utilisé pour établir un des outils les plus importants^[12] de la géométrie différentielle. Cet outil porte le nom de partition de l'unité. Il permet par exemple d'établir l'existence d'une densité sur une variété différentielle.

Démonstrations topologiques

Lemme d'Urysohn

La démonstration proposée ici s'appuie sur les fractions dyadiques^[13].

Soit D l'ensemble fractions dyadiques comprises entre 0 et 1, c'est-à-dire des rationnels de la forme k/2ⁿ, n étant un entier positif ou nul et k un entier variant de 0 à 2ⁿ. Pour tout r élément de D, on définit un ouvert U(r) tel que :

On procède pour cela par récurrence. Utilisant la propriété T₄ de l'espace topologique, soit U(0) un ouvert tel que B est inclus dans U(0) et l'adhérence de U(0) est incluse dans U(1), où U(1) désigne le complémentaire de A.

Si les U(r) sont construits pour tout r ayant un dénominateur inférieur ou égal à 2^n-1, considérons k impair. Par hypothèse de récurrence :

Une fois encore, la propriété T₄ permet de définir un ouvert U(k/2ⁿ) tel que :

On définit une fonction f de X dans [0, 1] tel que si x est élément de A, f(x) = 1 et sinon :

Par construction, f est égale à 1 sur A et à 0 sur B et est à valeurs dans [0,1]. Enfin, f est continue en tout point x. En effet, soit ε un réel strictement positif, x un élément de X, s et t deux éléments de D tels que f(x) = r et :

(Si r = 0, on prend s = 0, et si r = 1, on prend t = 1). La différence entre l'ensemble U(t) et l'adhérence de U(s) est un voisinage ouvert de x dont l'image par f est incluse dans [s,t]. (Si r = 0 on prend seulement U(t), et si r = 1, on prend seulement le complémentaire de l'adhérence de U(s)). La démonstration de la continuité de f complète la preuve.

Corollaire

Soit K une partie compacte d'un espace localement compact X. L'objectif est de montrer l'existence d'une fonction f continue, à support compact, qui vaut 1 sur K^[14]. Puisque X est localement compact, pour tout point k de K, il existe un ouvert U_k contenant k et dont l'adhérence est compacte. La famille (U_k) forme un recouvrement ouvert du compact K, donc il est possible d'en extraire un sous-recouvrement fini (U_kn). L'union des U_kn est un ouvert U contenant K et dont l'adhérence L est compacte donc normale. Le lemme d'Urysohn montre qu'il existe une fonction f_L, qui vaut 1 sur K et 0 sur le complémentaire de U dans L. On prolonge f_L par une fonction f, définie sur X et qui vaut 0 sur le complémentaire de L dans X. La fonction f est continue sur le fermé L, et nulle donc continue sur le complémentaire de U dans X. Elle est donc continue sur l'union X de ces deux fermés. Le support de la fonction f est un fermé du compact L, la fonction f est donc à support compact.

Démonstrations différentielles

Fonction plateau

Dans toute la suite de l'article E désigne un espace euclidien et n sa dimension. La démonstration du lemme d'Urysohn en géométrie différentielle demande la construction de fonctions plateau, analogue à celle illustrée sur la figure de droite. On cherche une application f_δ, où δ est un réel strictement positif, de E et à valeurs dans les nombres réels positifs, à support dans la boule fermée de centre le vecteur nul et de rayon δ, infiniment différentiable et d'intégrale sur E égale à 1^[15].

Pour construire une telle fonction, on bâtit d'abord la fonction illustrée en rouge sur la figure de gauche. Soit a et b deux nombres réels tels que a < b, on cherche à construire une application φ_ab définie sur R, à support égal à [a, b], infiniment dérivable et à valeurs dans les nombres réels strictement positifs. On définit la fonction φ_ab par :

Une rapide vérification montre que φ_ab est bien infiniment dérivable, à support égal à [a, b] et à valeurs positives. Comme elle est à valeurs strictement positives sur ]a, b[, l'intégrale dont la valeur est notée k^-1 est bien différente de 0.

On cherche alors à construire la fonction illustrée en bleu sur la figure de gauche. C'est une fonction ψ_ab de R dans l'intervalle [0, 1] qui vaut 1 pour toute valeur inférieure à a, 0 pour toute valeur supérieure à b et qui est infiniment dérivable. Pour la construire, il suffit de considérer la primitive de la fonction -k.φ_ab qui vaut 0 en b. La fonction f_δ est alors définie par :

Lemme

On suppose que E est un espace euclidien, K, illustré en vert sur la figure de gauche est un compact, Ω est un ouvert contenant K, en jaune sur la figure et on note ^cΩ, en rouge, le fermé complémentaire de Ω. L'objectif est de construire une application définie sur E, à valeurs dans [0, 1], qui vaut 1 sur K, 0 sur ^cΩ et infiniment différentiable. Cela revient à dire que la fonction g recherchée possède un graphe inclus dans la cage jaune de la figure en haut à droite (sauf sur la zone rouge où elle est nulle) et qu'elle recouvre le graphe de la fonction caractéristique que K, illustrée en bleu-vert sur la même figure. En termes plus mathématiques on obtient, si χ_K et χ_Ω désignent les fonctions caractéristiques de K et de Ω :

Considérons la fonction de K dans R₊, qui à x associe la distance entre x et ^cΩ. C'est une fonction continue, définie sur un compact, elle atteint sa borne inférieure. Si cette borne inférieure était nulle, elle serait atteinte en un point x adhérent à K et à ^cΩ. Comme ces deux ensembles sont fermés, x serait élément de K et de ^cΩ. Par définition de Ω, un tel point ne peut exister et la borne inférieure est strictement positive. Soit δ un réel strictement positif tel que 2.δ soit plus petit que cette borne inférieure (illustré sur la figure de gauche). On considère alors l'ensemble V, illustré en violet sur la figure de gauche, des points de E situés à une distance inférieure ou égale à δ de K. Par construction, tout point de ^cΩ est à une distance au moins égale à δ de V et toute boule de centre un point de K et de rayon δ est incluse dans l'ensemble V.

On considère la fonction caractéristique χ_V de l'ensemble V, illustrée sur la figure au milieu à droite et on définit g comme le produit de convolution de la fonction χ_V et f_δ du paragraphe précédent :

Comme les deux fonctions sont à support compact, l'intégrale est bien définie. Comme f_δ est une fonction infiniment différentiable, la fonction g l'est^[16]. Comme la fonction caractéristique est à valeurs positives comprises entre 0 et 1 et que f_δ est une fonction positive, d'intégrale sur E égal à 1, la fonction g prend ses valeurs dans l'intervalle [0, 1]. Si x est un élément de K, la fonction qui à t associe f_δ(x - t) est partout nulle, sauf sur la boule de centre x et de rayon δ. Si x est élément de K, cette boule est incluse dans V, on en déduit :

Si x est élément de ^cΩ, la fonction qui à t associe f_δ(x - t) est encore partout nulle, sauf sur la boule de centre x et de rayon δ. Sur cette boule, la fonction χ_V est nulle, on en déduit que sur le complémentaire de Ω, la fonction g est bien nulle. Cette remarque termine la démonstration^[3]. La fonction g est celle illustrée sur la figure en bas à droite.

Notes et références

Voir aussi

Bibliographie

(en) M. Henle, A combinatorial introduction to topology, Dover Publications (1994) (ISBN 0486679667)

Lien externe

G. Favi, Quelques idéaux maximaux de l'anneau des fonctions continues Journal de l'IMA, Université de Basel (Une démonstration de la version topologique)

• Portail des mathématiques