- Bulle De Savon
-
Bulle de savon
Même sujet vu par Chardin, XVIIIe siècle
Charles Joshua Chaplin, Blowing Bubbles, seconde moitié XIXe siècleUne bulle de savon est un globe formé d'un mince film d'eau savonneuse rempli d'air qui flotte dans l'atmosphère.
Sa paroi est constituée de deux rangées de phospholipides amphiphiles de par leurs "têtes" hydrophiles et leurs "queues" hydrophobes. Une étroite couche d'eau est retenue entre les têtes hydrophiles tandis que les queues hydrophobes, préférant le contact de l'air plutôt que celui de l'eau (comme leur nom l'indique), s'agencent de la manière suivante :
- queues de la rangée phospholipidique externe : tournées vers l'extérieur de la bulle, donc vers l'air ambiant.
- queues de la rangée phospholipidique interne : tournées vers l'intérieur de la bulle, donc vers l'air emprisonné.
Sommaire
Étude de la forme d'une bulle de savon
En raison de la tension superficielle, les films d'eau savonneuse sont dotés d'une certaine élasticité et il faut dépenser un peu d'énergie pour les étirer, comme on le fait sans s'en rendre compte lorsque l'on produit une bulle de savon. Ce phénomène peut, dans une certaine mesure, être comparé au gonflage d'un ballon de baudruche, à ceci près que le film d'eau savonneuse est constitué de liquide et que l'énergie mise en jeu pour produire une bulle est beaucoup moins importante. Il reste que la pression du gaz contenu dans une bulle est légèrement plus forte que celle de l'atmosphère environnante.
Plus l'aire d'un film liquide est importante, plus son énergie potentielle est élevée. Or, tout système matériel atteint un équilibre stable lorsque son énergie potentielle est minimale. Une bulle de savon tend donc, naturellement, à prendre la forme qui lui permet d'enfermer un volume d'air donné dans une surface d'aire minimale ; tout le monde a pu constater qu'il s'agit d'une sphère, mais constater n'est pas démontrer et les mathématiciens, Archimède en tête, s'y sont longtemps cassé les dents. Il fallut attendre 1882 pour que le mathématicien allemand Hermann Amandus Schwarz prouve que parmi toutes les surfaces enfermant un volume donné, la sphère est bien celle qui présente l'aire minimale (cf l'article Isopérimétrie).
On peut généraliser ce problème : étant donnés deux volumes Va et Vb, quelle est la surface minimale susceptible de les contenir ? L'observation incite à penser qu'il s'agit d'une double bulle, limitée par deux portions de sphère, avec un « disque » de séparation bombé ou non. Ceci n'a cependant été prouvé qu'en 1995, et encore, dans le cas de deux volumes égaux...
Beaucoup de problèmes mathématiques très ardus ont pourtant des énoncés extrêmement simples...
Les lois de Plateau
Le problème se complique singulièrement lorsque l'on a affaire à une mousse formée d'un très grand nombre de bulles accolées. Le physicien belge Joseph Plateau, dans la seconde moitié du XIXe siècle, énonça quatre lois simples, tirées de l'observation des bulles, jamais démenties, et qui portent son nom :
- tout film enfermant des bulles se compose d'éléments de surface lisses,
- la courbure moyenne de chacun de ces éléments est constante (ce ne sont pas forcément des sphères),
- lorsque trois éléments de surface se rejoignent, ils se raccordent selon une courbe régulière en tout point de laquelle leurs plans tangents forment des angles de 120°,
- lorsque ces lignes de raccordement se rejoignent, elles le font quatre par quatre et prennent alors, au point de rencontre, les quatre directions tétraédriques (comme les quatre segments qui joignent le centre d'un tétraèdre régulier à ses sommets, et dont chacun forme avec les autres des angles d'environ 109°).
Pression intérieure
Deux bulles ou double bulle ?Pour passer de l'extérieur à l'intérieur d'une bulle de savon, nous devons traverser deux surfaces de changement de milieu. En vertu de la loi de Laplace, nous en déduisons la pression à l'intérieur d'une bulle de savon. Elle est donnée par la formule :
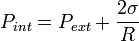
Pint étant la pression à l'intérieur de la bulle.
Pext étant la pression à l'extérieur de la bulle.
σ étant la tension superficielle.
R étant le rayon de la bulle de savon.
Iridescence d'une bulle de savon.Couleurs observées sur une bulle de savon
Lorsque nous observons une bulle de savon en plein jour, nous pouvons voir des irisations rappelant les couleurs de l'arc-en-ciel. Pourtant le phénomène a une origine totalement différente. Ce phénomène d'iridescence est dû à des interférences entre les rayons se réfléchissant sur la surface extérieure de la bulle et les rayons se réfléchissant sur la surface intérieure de la bulle.
Recettes pour faire des bulles de savon géantes
Les petits tubes vendus dans le commerce avec un cercle fixé au bouchon, que l'on trempe et retrempe dans le produit liquide d'origine, donnent généralement d'honnêtes bulles d'environ 5 cm de diamètre. D'autres, meilleurs, produisent des bulles nettement plus grosses, pouvant atteindre 15 ou 20 cm, ou davantage. Une fois le produit épuisé, on essaie souvent de le remplacer par de l'eau savonneuse ou du produit à vaisselle, et... ça ne marche pas !
Un bon début !Quel est donc le secret des belles bulles ? Les spécialistes sont à peu près d'accord sur la composition du liquide.
De nombreuses recettes circulent sur Internet : la plupart d'entre elles recommandent l'utilisation de glycérine pour épaissir le mélange et assurer la stabilité des bulles de grande taille.
Pour obtenir 100 ml, il faut mélanger dans l'ordre :
- 25 ml d'eau distillée (de l'eau très peu minéralisée convient également)
- 5 grammes de sucre (une à deux cuillères à café de sucre) (du sucre glace est parfois conseillé)
- 20 ml de liquide de vaisselle
- 10 ml de glycérine On peut facilement en acheter en pharmacie
- 40 ml d'eau distillée. L'ajouter à la fin permet un meilleur mélange et moins de mousse.
Le produit "mir" est souvent conseillé également. Voir les liens externes pour plus de conseils, par exemples sur la marque du produit de vaisselle
Voici une recette générale pour faire des bulles de savon géantes:
- 1 volume de liquide vaisselle
- 12-14 volume d'eau
- 1/4 de volume de glycérine
Si vous n'avez pas de glycérine, une alternative intéressante à ce produit est l'amidon de maïs contenu dans la « levure chimique ». C'est David Stein, faiseur de bulles géantes, qui l'a popularisée. Cette recette a l'avantage de revenir à un prix modique. Dans ce cas, ajoutez 1 cuillère à soupe de « levure chimique » pour 1 volume de liquide vaisselle.
Un autre ingrédient particulièrement important est le liquide vaisselle. Les multiples essais et la pratique des bulleurs du monde entier ont permis de constater que les produits vaisselle du groupe Procter & Gamble — « Dreft » est la marque habituelle en Europe — offrent les meilleurs résultats.
Les conditions climatiques sont déterminantes, elles aussi, pour la stabilité des bulles. Plus l'air est humide, plus les bulles seront grosses et auront une longue durée de vie. C'est pourquoi les meilleurs moments pour buller sont à l'aube et pendant la nuit, quand l'humidité est la plus haute. Se trouver à proximité d'un fleuve, d'un étang ou dans une forêt favorise l'humidité de l'air.
Production automatique de bulles de savon
Petit générateur de bullesPour des raisons ludiques et festives, ont été développés quelques modèles de petites machines générant des bulles en continu.
La pratique des bulles de savon géantes
Les champions parviennent à produire des bulles d'un mètre et plus.
Bulle-tube géante Il faut savoir manier la ficelle et les baguettes, et ne pas hésiter à s'entraîner et à utiliser un grand nombre de litres de « sauce » avant de vouloir briller en public.
Bulle-tube Voir aussi
- Les Bulles de savon, d'Édouard Manet (1867).
- Gouttes, bulles, perles et ondes, P-G. de Gennes, F. Brochard-Wyart, D. Quéré, (Belin Échelles, 2002) (ISBN 2701140552)
liens externes
- Bubble solutions en anglais
- Soap bubbles sur wikipedia en anglais
Catégories : Mécanique des milieux non homogènes | Enfance
Wikimedia Foundation. 2010.
