- Histoire des équations
-
Cet article décrit les faits marquants de l'histoire des équations de l'Antiquité à aujourd'hui.
De l'Antiquité à la Renaissance
L'Antiquité
 Le livre arithmetica de Diophante est le premier à décrire l'ajout d'une lettre à un ensemble de nombres.
Le livre arithmetica de Diophante est le premier à décrire l'ajout d'une lettre à un ensemble de nombres.
- Egypte ancienne et Babylone
Aussi loin que remontent les textes connus en mathématiques, on y trouve des questions que l'on modéliserait aujourd'hui par des équations algébriques. On lit, dans un papyrus de l'Égypte ancienne : « Quand le scribe te dit 10 est les 2/3 et le 1/10 de quoi ? »[1], ce qui pourrait se traduire par
 . Aucun outil algébrique n'est alors développé. Les égyptiens résolvent l'équation du premier degré par tâtonnement et les babyloniens disposent d'algorithmes mais sans justification autre que l'expérience.
. Aucun outil algébrique n'est alors développé. Les égyptiens résolvent l'équation du premier degré par tâtonnement et les babyloniens disposent d'algorithmes mais sans justification autre que l'expérience.- Empire romain
Au Ier siècle apr. J.-C., les écrits de Héron d'Alexandrie décrivent une méthode permettant l’approximation de la racine positive d’une équation telle que x2 = 2.
- Chine
En 263 Liu Hui, mathématicien chinois publia une estimation de π à 3,1416[2] à l'aide d'une méthode itérative.
- Première théorie
La première étape qui rapproche de l'ébauche d'une véritable théorie est franchie indépendamment par trois cultures mathématiques : la Grèce, la civilisation arabe et celle des Indes.
Diophante, un mathématicien du IIIe siècle, formalise l’arithme, une lettre qu'il définit[3] comme : « Le nombre qui possède une quantité indéterminée d’unités s’appelle l’arithme, et sa marque distinctive est σ. ».
Le Moyen Âge
- Inde et Moyen-Orient
Avant que Diophante ne soit traduit en arabe[4], Al-Khawarizmi, 783 - 850, un mathématicien d'origine perse, développe au VIIIe siècle une idée analogue. Son inconnue s'appelle le say' [5]. La même idée est encore présente chez le mathématicien indien Bhāskara II, dans son texte intitulé Bījagaṇita[6].
 Les polynômes d'al-Samaw'al représentés par un tableau préfigurent une conception purement abstraite de l'algèbre.
Les polynômes d'al-Samaw'al représentés par un tableau préfigurent une conception purement abstraite de l'algèbre.
Les travaux d'Al-Khawarizmi sont souvent considérés comme l'acte de naissance de la branche des mathématiques appelée algèbre. En termes d'étymologie, le titre de son traité sur les équations : Kitâb al-jabr wa al-muqâbala utilise le terme al-jabr, devenu algèbre.
En arabe, al-jabr « correspond à transformer une soustraction dans un membre en une addition dans l'autre membre »[7] dans l'objectif d'obtenir uniquement des coefficients positifs. Par exemple[8] : 2x2 + 100 - 20x = 58 devient par al-jabr : 2x2 + 100 = 58 + 20x.
Le travail d'Al-Khawarizmi est l'acte de naissance d'une théorie des équations quadratiques, dans l'ensemble des nombres positifs (presque toujours rationnels)[9]. Al-Khawarizmi s'intéresse à toutes les équations du second degré alors que Diophante ne cherchait à résoudre que celles ayant des solutions, soit entières, soit rationnelles. Al-Khawarizmi est systématique, l'objet de son traité est d'offrir une méthode permettant de trouver à coup sûr, s'il en existe, une solution de l'équation.
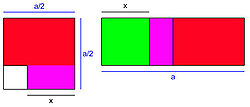 Les gnomons et la géométrie d'Euclide sont le moteur de la résolution des équations algébriques pendant plusieurs siècles.
Les gnomons et la géométrie d'Euclide sont le moteur de la résolution des équations algébriques pendant plusieurs siècles.
La géométrie, et particulièrement celle des Éléments d'Euclide, écrits vers -300, joue un rôle fondamental dans cette algèbre naissante. Si l'angle d'analyse des arabes est différent, puisqu'ils cherchent à résoudre une équation, dans ce cas particulier du second degré, le cœur de la démonstration est le même : une analyse d'une configuration géométrique, construite sur la base d'un gnomon.
Omar Khayyam remarque qu'il est possible d'interpréter la racine de l'équation cubique comme l'abscisse de l'intersection d'un cercle et d'une parabole[10]. Ce qui montre déjà l'usage de ce que l'on appellera plus tard un repère cartésien et permet de remarquer l'existence possible de plusieurs solutions[11]. Deux siècles plus tard, profitant des progrès tant algébrique que géométrique, Nasir ad-Din at-Tusi développe plusieurs outils de la théorie des équations dans le cadre de l'équation cubique. Son successeur Sharaf al-Dîn al-Tûsî (XIIe siècle) va étudier de façon plus rigoureuse les conditions d’existence de solutions ; ceci va l’amener à se pencher sur des problèmes de localisation et de séparation des racines, l’obliger à définir la notion de maximum d’une expression algébrique (en introduisant la dérivée formelle d’un polynôme). Une autre innovation d’al-Tûsî consiste à traiter, en même temps que la résolution géométrique, la résolution numérique des équations du troisième degré.
- Europe
Vers l'an mil, le pape Sylvestre II fait adopter les chiffres arabes issus de la numération indienne.
- Extrême-Orient
En parallèle avec l'Europe et le Moyen-Orient, en Chine des algorithmes de résolution d'équations sont développés.
Un système de résolution d'équations linéaires aurait été publié dès la Dynastie Han, mais elle n'étend pas la définition des nombres aux valeurs négatives. Cette information n'est plus mentionnée durant des siècles et pourrait avoir été partiellement oubliée[12].
En 1303, Zhu Shijie, mathématicien chinois publie Miroir précieux des quatre éléments qui inclut une explication de sa méthode des quatre éléments, qui sont utilisés pour signifier quatre quantités inconnues dans une seule équation algébrique. Il inclut les nombres négatifs[13]. Ce savoir semble s'être à nouveau estompé jusqu'à l'arrivée des jésuites en Chine à la fin du XVIe siècle.
La Renaissance
- Europe
Vers 1450, Johannes Gutenberg invente l'imprimerie, permettant dès le début du XVIe siècle de diffuser les documents écrits à une très large échelle. À travers l'impression des textes de Fibonacci ou encore de Luca Pacioli, l'Italie a accès à l'essentiel du savoir arabe. Les mathématiciens d'alors se passionnent pour l'algèbre et surtout, pour le problème encore laissé ouvert : trouver une méthode générale et exacte de résolution de l'équation cubique.
Scipione del Ferro trouve comme formule de résolution de l'équation X3 + aX = b :
![x= \sqrt[3] {\frac b2 + \sqrt {\left(\frac b2\right)^2 + \left(\frac a3\right)^3}} + \sqrt[3] {\frac b2 - \sqrt {\left(\frac b2\right)^2 + \left(\frac a3\right)^3}}](3/16355c2c9eb2d8ec58af9a6535fb73b4.png)
Une question reste ouverte, comment résoudre l'équation X3 + b = aX si 4a3 > 27b2 ? Tartaglia, un maître en la matière, qualifie l'équation d' irréductible. Girolamo Cardano généralise la formule de Tartaglia et lui adjoint des nombres imaginaires pour résoudre des cas qualifiés alors d'irréductibles.
Une nouvelle étape est franchie dans la théorie des équations. Si la signification précise de l'expression
 reste mystérieuse, l'idée de faire appel à un ensemble de nombres plus grand pour résoudre une question en théorie des équations est découverte. Un élève de Cardano, Ludovico Ferrari finit par résoudre l'équation quartique, en 1540[14]. Bombelli propose un formalisme autorisant l'existence de nombres négatifs et imaginaires.
reste mystérieuse, l'idée de faire appel à un ensemble de nombres plus grand pour résoudre une question en théorie des équations est découverte. Un élève de Cardano, Ludovico Ferrari finit par résoudre l'équation quartique, en 1540[14]. Bombelli propose un formalisme autorisant l'existence de nombres négatifs et imaginaires.L'article Méthode de Cardan présente la solution, en terme contemporain, de l'équation cubique et celui intitulé Méthode de Ferrari celle du quatrième degré.
- Extrême-Orient
Vers 1590, une mission jésuite, dont fait partie Matteo Ricci, arrive en Chine et échange des informations scientifiques avec les savants de la Dynastie Ming. Il faut savoir que la capacité à déterminer les faits célestes avec précision sont essentiels au pouvoir de l'empereur de Chine et les jésuites utilisent leurs compétences en horlogerie et en géométrie pour accéder à la cité interdite et avoir les faveurs de l'empereur[15]. Mei Wending comparera le savoir obtenu des occidentaux au savoir ancestral des chinois et conclura[16]:
« J'ai commencé à me persuader que les différentes constructions de la géométrie étaient compréhensibles, tandis qu'eux [les Occidentaux] en font un enseignement secret des Dieux, et que nous [Chinois] les rejetons en tant qu'hérésie. Ni les uns ni les autres n'ont sur la géométrie un jugement équilibré. »
Les équations différentielles
La résolution mécanique
 Kay McNulty, Alyse Snyder, et Sis Stump utilisant l'analyseur différentiel dans les sous-sols de la Moore School of Electrical Engineering à l'université de Pennsylvanie en Philadelphia, vers 1942-1945.
Kay McNulty, Alyse Snyder, et Sis Stump utilisant l'analyseur différentiel dans les sous-sols de la Moore School of Electrical Engineering à l'université de Pennsylvanie en Philadelphia, vers 1942-1945.
Comme le dit lui-même Newton,
« il est utile de résoudre des équations différentielles. »
Dès lors que l'analyse pris son essor sous l'impulsion de Newton, Leibniz et des Bernoulli, on s'est préoccupé de résoudre des problèmes de géométrie avec cet outil. Et plus encore, avec des outils mécaniques. De 1692 à 1752, pendant soixante ans, on a développé toute une industrie mécanique destinée à résoudre graphiquement les équations différentielles. Le traité de Vincenzo Riccati, De usu motus tractorii in constructione æquationum differentialium, publié en 1752 est à ce titre tout à fait remarquable d'une technique ayant atteint son sommet et qui va disparaître totalement dans les méandres du temps au point que lorsque de nouveau le besoin se fait sentir d'avoir des outils mécaniques, les intégraphes, entre 1880 et 1920, on retrouvera les anciennes solutions sans savoir que de telles solutions existaient plus d'un siècle avant. L'analyseur différentiel est l'aboutissement de cette méthode.
La résolution analogique
De la même manière, on a cherché à résoudre de manière analogique les équations aux dérivées partielles en se servant des phénomènes physiques à l'origine de ces équations. Ainsi, l'équation de Laplace se résout-elle par une analogie électrique et cette méthode était enseignée au niveau universitaire au moins au milieu des années 1970. Des calculateurs électroniques analogiques ont vu le jour. Le premier par Helmut Hoelzer date de la fin des années 1930 et du début des années 1940 pour les études des V1, V2, et V3 du Troisième Reich. L'élément essentiel de ces dispositifs à lampes, ou à transistors par la suite, est l'amplificateur opérationnel.
Les équations différentielles au XVIIe siècle et au XVIIIe
Les problèmes posés ou menant à des équations différentielles sont aussi vieux que l'analyse elle-même. Avant même qu'on ait complètement élucidé la question des infiniment petits et trouvé des fondements (provisoires), l'on se préoccupe déjà de résoudre des problèmes de tangente, qui mènent invariablement à une équation différentielle. De la même manière, dès les débuts de la mécanique classique, dite newtonienne, on cherche à résoudre des problèmes de n points matériels qui tous mènent à l'intégration d'un système de 3n équations différentielles du second ordre, où les inconnues sont des fonctions du temps représentant des coordonnées des points.
On s'habitue progressivement à ce que l'inconnue d'une équation puisse être une fonction. La fonction a encore à cette époque, et pour longtemps un statut flou. Même les fonctions élémentaires ne sont pas exemptes de problèmes. Une longue polémique occupe toute l'Europe mathématique sur la question des logarithmes des nombres négatifs. Leibniz s'oppose ainsi à Euler qui est le seul à entrevoir la bonne réponse.
Pour un mathématicien de la fin du XVIIe siècle ou du début du XVIIIe, résoudre une équation différentielle consiste à écrire la solution générale de l'équation, et de préférence en termes finis et avec des fonctions élémentaires. Il n'est ici pas question de problème de conditions initiales.
On utilise à cette époque, sans formalité, la méthode des séries entières pour résoudre les équations différentielles. On ne se préoccupe aucunement de la convergence de ces séries qui sont censées converger tout le temps. Même Euler, le plus grand mathématicien du XVIIIe siècle, ne voit pas le problème. Il va jusqu'à intégrer et dériver des séries dont le rayon de convergence est 0, sans même s'apercevoir qu'il a trouvé ainsi des contre-exemples à la croyance de l'époque que la série de Taylor converge. Quand il est confronté au calcul numérique sur de telles séries non convergentes, son flair de mathématicien lui indique qu'il convient de s'arrêter au terme le plus faible en valeur absolue. Les séries asymptotiques ne sont pas loin mais il faudra encore du temps pour la conceptualisation de la question qui ne sera réellement abordée qu'un siècle plus tard. Stirling de son côté, avec de Moivre, interpolent la fonction factorielle dont Euler donnera une représentation intégrale. Là encore, il s'agit d'un développement asymptotique.
Une autre question qui occupe beaucoup est d'écrire les solutions des équations différentielles en ne faisant intervenir que des expressions finies de fonctions élémentaires. Leibniz est ainsi le prometteur de la méthode de décomposition en éléments simples. Le nombre des équations qu'on sait résoudre à cette époque par cette voie, quoiqu'en constante augmentation, est tout de même assez faible. Par exemple, les Bernoulli savent intégrer l'équation linéaire et quelques autres du premier ordre. À cette courte liste, Riccati va apporter en 1722, un nouveau cas.
Pour les équations différentielles du premier ordre de la forme P(x,y)dx + Q(x,y)dy = 0, Alexis Clairaut utilise pour la première fois un multiplicateur, une fonction M(x,y) telle que le produit par l'équation en fasse une différentielle totale exacte dV(x,y) = 0 ce qui permet de l'intégrer sous la forme V(x,y) = Constante. Euler développera cette méthode.
Clairaut est le premier, en 1734, à remarquer, sur l'équation y − xy' + f(y') = 0, l'existence d'une solution singulière. À la famille de droites y = Cx + f(C) qui est l'expression générale des courbes intégrales, il faut adjoindre l'enveloppe de cette famille pour avoir toutes les solutions analytiques de l'équation. D'Alembert, en 1748, trouve un second cas d'intégrale singulière. Mais c'est Euler et Lagrange qui élucident ce qui se passe en général en montrant que la courbe C(x,y) = 0 obtenue en éliminant y' entre les deux équations F(x,y,y') = 0 et
 est en général le lieu des points singuliers des courbes intégrales de l'équation F(x,y,y') = 0. Si elle vérifie l'équation
est en général le lieu des points singuliers des courbes intégrales de l'équation F(x,y,y') = 0. Si elle vérifie l'équation  , la courbe C(x,y) = 0 est solution singulière de l'équation.
, la courbe C(x,y) = 0 est solution singulière de l'équation.Si l'on sait, dès la fin du XVIIe siècle intégrer les équations différentielles linéaires du premier et du second ordre à coefficients constants par des sommes d'exponentielles, il faut attendre 1760 pour que la théorie vienne à bout des équations différentielles linéaires à coefficients constants d'ordre quelconque. En 1739, Euler rencontre une équation différentielle linéaire à coefficients constants du 4e ordre sur un problème de vibration des tiges qu'il ne sait pas intégrer. C'est en 1743 qu'il forme ce qu'on appelle aujourd'hui l'équation caractéristique : les solutions sont de la forme erx où les r sont solutions d'une équation polynomiale. Un peu plus tard, il trouve comment obtenir toutes les intégrales lorsqu'une racine r de l'équation caractéristique est multiple : il faut les chercher de la forme xkerx.
D'Alembert remarque que pour les équations différentielles linéaires non homogènes, l'adjonction d'une solution particulière à la solution générale de l'équation homogène donne la solution générale de l'équation homogène. Lagrange démontre que la solution générale d'une équation différentielle linéaire d'ordre n est de la forme
 où les yk sont des solutions particulières convenablement choisis de l'équation. Lagrange introduit également la méthode de variation des constantes pour résoudre par quadratures l'équation linéaire non homogène lorsque l'on connaît la solution générale de l'équation homogène. D'Alembert, de son côté, remarque que si l'on connaît une solution particulière y1, en posant y = zy1, on ramène l'intégration d'une équation linéaire d'ordre n homogène à une équation du même type d'ordre n-1 en z : il y a abaissement de l'ordre.
où les yk sont des solutions particulières convenablement choisis de l'équation. Lagrange introduit également la méthode de variation des constantes pour résoudre par quadratures l'équation linéaire non homogène lorsque l'on connaît la solution générale de l'équation homogène. D'Alembert, de son côté, remarque que si l'on connaît une solution particulière y1, en posant y = zy1, on ramène l'intégration d'une équation linéaire d'ordre n homogène à une équation du même type d'ordre n-1 en z : il y a abaissement de l'ordre.Pour les équations linéaires, Euler utilise aussi des séries entières. Il remarque alors qu'il faut parfois des développements de la forme
 où S(x) est une série entière et λ un exposant non entier. Ceci près d'un siècle avant les travaux de Fuchs et de Frobenius. Pour l'équation du second ordre, il sait former l'équation déterminant λ et observe aussi, dans le cas où λ est entier qu'il existe une second solution avec un terme logarithmique.
où S(x) est une série entière et λ un exposant non entier. Ceci près d'un siècle avant les travaux de Fuchs et de Frobenius. Pour l'équation du second ordre, il sait former l'équation déterminant λ et observe aussi, dans le cas où λ est entier qu'il existe une second solution avec un terme logarithmique.En mécanique, la question se concentre essentiellement autour du problème des n corps de la mécanique céleste. Les 3n équations différentielles sont traitées à partir de la solution keplerienne : on néglige d'abord tous les autres corps sauf deux, le corps dont on étudie le mouvement et le Soleil. Les autres corps apparaissent ensuite comme affectés de petits paramètres. On développe les solutions en séries entières et on essaie, autant que possible, d'éviter l'apparition de termes non périodiques. Clairaut, D'Alembert, Euler, Lagrange et Laplace consacrent de nombreux mémoires afin de démontrer la stabilité du système solaire. La stabilité est plausible mais non démontrée à grande échelle.
Le premier exemple du problème de Sturm-Liouville est donné par D'Alembert à propos de la vibration d'une corde non homogène. D'Alembert considère une équation différentielle y'' = ma(x)y, dont la solution répond à la condition aux limites y(0)=y(a)=0 et où m est un paramètre dont il cherche la valeur afin que la solution ne s'annule pas dans l'intervalle ]0,a[. Il forme l'équation de Riccati associée et montre, avec quelques trous dans son raisonnement, qu'il n'existe qu'une seule valeur de m répondant à la question.
L'équation de Riccati, phase I: de Riccati à Euler
L'équation différentielle de Riccati est de la forme y' = a(x)y2 + b(x)y + c(x). On peut la voir comme une équation différentielle y' = f(x,y) dont on aurait développé la fonction f(x,y) en y à l'ordre deux.
Initialement elle est d'une forme plus simple, y' = ay2 + bxn. Bien qu'étudiée par Jacques Bernoulli, cette équation différentielle porte le nom de Jacopo Riccati, un hydraulicien et mathématicien qui s'intéressa à cette équation longtemps avant d'en proposer la résolution à ses collègues, en 1724. Il est connu, à cette époque, pour avoir intégré par réduction de l'ordre et séparation des variables certaines équations différentielles. Son problème fait aussitôt réagir les Bernoulli : l'équation a été étudiée par plusieurs d'entre eux et ils connaissent un cas d'intégration par quadrature. Mais on sait que Jacopo Riccati connait également, et depuis longtemps, le cas d'intégration par quadrature. Cette équation ne s'intègre ainsi que si n est égal à 2 ou de la forme -4m/(2m+1) ou -4m/(2m-1), m étant un entier positif ou nul.
Cependant, chacun cherche une solution par quadrature dans les autres cas. Quand l'encyclopédie de Diderot et d'Alembert paraît en 1751, on lit à ce propos
« RICATI (équation de) Algèbre. Calcul intégral. On appelle ainsi une équation différentielle du premier ordre à deux variables que le comte Ricati proposa aux géomètres vers 1720, & dont personne n'a encore donné de solution générale. Peut-être n'est-elle pas susceptible d'en avoir une en termes finis.
Cette équation est de la forme dy + y2dx + axmdx = 0. On a trouvé que toutes les fois m = (- 4 h)/(2 h ± 1), h étant un nombre entier positif, la proposée se réduisoit à dy' + y'2dx' + a'dx' = 0, d'où l'on tire a'dx' = − (sdy') / (1 + y'2), pour le prouver, il suffit de faire y égal à
 & x = a'x'n, & on trouvera des valeurs de q, r, & c. telles que la réduction ait lieu, la valeur de y en y'& x' n'étant qu'en nombre fini de termes. »
& x = a'x'n, & on trouvera des valeurs de q, r, & c. telles que la réduction ait lieu, la valeur de y en y'& x' n'étant qu'en nombre fini de termes. »Effectivement, cette équation ne se laisse généralement pas résoudre par des quadratures indéfinies.
Euler a montré, en 1760, qu'un changement de variable de la forme y(x) = − w'(x) / a(x)w(x) transforme l'équation de Riccati en une équation différentielle du second ordre linéaire en w:
a(x)w'' − (a'(x) + b(x)a(x))w + a2(x)c(x)w = 0. Et inversement, il sait transformer une équation différentielle linéaire du second ordre en une équation de Riccati, ce qui lui permet parfois de l'intégrer par quadrature.
Euler et Lagrange se servent de la propriété qu'une équation de Riccati se transforme en une autre équation de Riccati en posant la solution fonction homographique (à coefficients fonctions de x) d'une autre inconnue, pour développer la solution en fraction continue.
L'équation de Riccati, phase II : la théorie galoisienne
Émile Picard avait montré l'existence d'un groupe continu de transformations linéaires homogènes à n variables pour chaque équation linéaire d'ordre n, ce groupe jouissant de propriétés semblables à celles du groupe de substitutions d'une équation algébrique[17],[18]. Dans sa thèse[19] soutenue en 1892, Vessiot pose les fondements de la théorie galoisienne des équations différentielles linéaires. Il démontre ainsi les théorèmes suivants
« Pour qu'une équation linéaire soit intégrable par quadrature il faut et il suffit que le groupe de transformations de cette équation soit intégrable[20] »
« L'équation différentielle générale d'ordre n (n>1) n'est pas intégrable par quadratures[21] »
« Si une équation linéaire est intégrable par quadratures, la dérivée logarithmique de l'une de ses intégrales s'exprime rationnellement[22], »
résultat démontré auparavant par Liouville dans le cas de l'équation différentielle d'ordre 2 du type y'' = Py, P étant un polynôme en x[23].
Cela permet de conclure que l'équation de Riccati n'est en général pas résoluble par quadrature. On a montré aussi que la solution générale d'une équation de Riccati est une fonction homographique de la constante d'intégration.
La résolution par quadrature : le renouveau moderne
La question de la résolution d'une équation différentielle en termes finis est un vieux problème. Painlevé, en 1904, déclarait
« La vague s'arrêta quand tout ce qui était intégrable, dans les problèmes naturels fût intégré[24], »
et il croyait cette question définitivement résolue[Note 1]. On pensait que jamais on ne pourrait trouver un algorithme permettant de savoir si une équation différentielle est résoluble par une formule. Cependant, cette question a reçu aujourd'hui un regain certain d'intérêt. On sait déterminer depuis une cinquantaine d'années si une équation différentielle admet une solution exprimable par une formule ou s'il faut se contenter d'un calcul numérique. C'est la résolution en forme close, suite aux travaux de Oystein Ore[25], dans les années 1930, sur les polynômes non-commutatifs. L'introduction des bases de Gröbner a permis la réalisation d'algorithmes bien adaptés aux calculs formels, tant sur les équations différentielles elles-mêmes que sur les équations aux dérivées partielles. Des logiciels puissants ont été réalisés depuis 1980 qui étendent considérablement les moyens de calcul des ingénieurs. Mais ils restent cependant encore limités aux équations les plus simples. En mécanique des fluides, par exemple, cela ne permet pas d'étudier des modèles de turbulence.
Les théorèmes d'existence et d'unicité
Les mathématiciens du XVIIIe siècle admettent sans discussion l'existence de solutions des équations différentielles ou aux dérivées partielles sans chercher le domaine d'existence de ces solutions. Ils utilisent principalement des séries entières par une méthode de coefficients indéterminés quand ils n'arrivent pas à intégrer l'équation par quadrature. Leur confiance est placée dans le théorème de Taylor et ils ne se posent pas la question de la convergence de cette série. Ils savent, par contre, que la donnée d'un point et de la fonction en ce point ainsi que ses n-1 dérivées détermine la solution de l'équation différentielle y(n) = f(x,y,y',...,y(n − 1)).
Il faut attendre Cauchy, vers 1820, pour que soit abordée l'existence d'une solution à l'équation différentielle y' = f(x,y), où f est supposée continument différentiable en chaque variable. Il s'agit de prouver qu'étant donné un point (x0,y0) il existe une solution et une seule qui satisfait à l'équation différentielle et qui passe par ce point, cette fonction étant définie sur un petit intervalle autour de x0. Évidemment, on ne se pose encore pas la question des solutions complexes. Il s'agit donc pour Cauchy, contrairement à ses devanciers, d'un problème d'existence et d'unicité local puisqu'on ne sait pas jusqu'où la solution se prolonge. Pour cela Cauchy reprend la méthode d'Euler à un pas h. Il calcule ainsi une solution approchée, affine par morceaux, de l'équation et il peut, utilisant le théorème de la moyenne, majorer la différence entre deux solutions approchées pour deux pas h et h' différents, en fonction de f et de x0 et y0 mais non du pas la différence. Il démontre ainsi que la solution approchée uh(x) tend vers une fonction u(x) qui est l'unique solution de l'équation quand h tend vers 0. Sa démonstration s'applique, il le remarque, pour les systèmes d'équations différentielles de sorte qu'il obtient un théorème d'existence et d'unicité pour les équations différentielles d'ordre quelconque.
Sans connaître les travaux de Cauchy, Lipschitz, en 1868, retrouve le résultat de Cauchy mais, là où Cauchy avait supposé la différentiabilité de f, Lipschitz remarque qu'elle n'est nullement nécessaire et qu'il suffit qu'il existe un nombre k strictement positif tel que | f(x,y1) − f(x,y2) | < k | y1 − y2 | . C'est la condition de Lipschitz.
En 1837, Liouville utilise, pour le cas particulier d'une équation linéaire du second ordre une méthode d'approximation successive : on détermine une suite de fonctions en posant u(x0)=y0 et en utilisant la récurrence un'(x) = f(x,un − 1(x)). Si la condition de Lipschitz est satisfaite, les un(x) sont définies dans un voisinage de x0 et convergent uniformément vers la solution u de l'équation, avec u(x0)=y0. D'après l'abbé Moigno, Cauchy aurait également utilisé ce procédé vers la même époque. Mais ce procédé tombe dans l'oubli jusqu'en 1870 où il réapparaît sous la plume de Carl Neumann, et de Hermann Amandus Schwarz à propos du problème de Dirichlet. C'est Émile Picard qui va montrer la fécondité de la méthode des approximations successives, à partir de 1890, en l'appliquant à de très nombreux problèmes d'existence pour des équations fonctionnelles. Par la suite, Banach formulera la méthode dans un cadre général.
Émile Picard montre en outre que la méthode des approximations successives fournit une solution holomorphe au voisinage de (x0,y0) lorsque le second membre est lui-même analytique. Ce résultat, obtenu par Cauchy en 1831, justifiait pleinement le procédé des séries formelles des analystes du XVIIIe siècle. Mais Cauchy obtenait son résultat de la méthode des majorantes (qu'il appelait « calcul des limites ») : Si on développe au voisinage de (x0,y0) la fonction f(x,y) en série entière double, on a
f(x,y) = ∑ ∑ cn,m(x − x0)n(y − y0)m. n m La fonction f(x,y) est "majorée" par F(x,y) au voisinage de (x0,y0) si les coefficients du développement de f(x,y) sont majorés par ceux du développement de F(x,y). On a donc
 .
.(en travaux)
Les équations différentielles linéaires ordinaires à coefficients variables. La théorie de Fuchs
En 1866, Fuchs étudia[26] les points singuliers des solutions d'une équation différentielle ordinaire à coefficients variables dont on peut séparer la dérivée d'ordre le plus élevé. Il s'intéressa aux solutions qui sont développables en série au voisinage d'un point singulier des coefficients.
Soit P(x)y'' + Q(x)y' + R(x) = 0 une équation différentielle à coefficients variables du second ordre. Si a est un point régulier de Q(x) / P(x) et R(x) / P(x),le point est dit régulier. La solution est développable en série entière convergente au voisinage de a. Autrement a est un point singulier.
Si a est un point singulier tel que (x − a)Q(x) / P(x) ainsi que (x − a)2R(x) / P(x) soient développables en séries entière convergentes, alors a est appelé point singulier régulier. Autrement le point a est dit singulier irrégulier.
On obtient dans ce cadre le théorème suivant dû à Fuchs :
« Si a est un point régulier, il existe une unique solution développable en série entière dans le disque | x − a | < r où r est le plus petit des rayons de convergence des séries entières de Q(x) / P(x) et R(x) / P(x).
Si a est un point singulier régulier, il existe une unique solution développable en série entière dans le disque | x − a | < r, où r est le plus petit des rayons de convergence des séries entières de
 et
et  . »
. »On cherchera ainsi des solutions de la forme
 , c étant un réel. C'est par exemple ainsi qu'on résout l'équation de Bessel[27]. Les fonctions de Bessel qui sont des solutions des équations de Bessel sont des oscillations amorties, elles se retrouvent en particulier dans les systèmes diffractés (optique, physique corpusculaire, électromagnétisme).
, c étant un réel. C'est par exemple ainsi qu'on résout l'équation de Bessel[27]. Les fonctions de Bessel qui sont des solutions des équations de Bessel sont des oscillations amorties, elles se retrouvent en particulier dans les systèmes diffractés (optique, physique corpusculaire, électromagnétisme).Les équations différentielles sans point critique fixe
La résolution des équations différentielles avait montré que les solutions dépendaient des constantes d'intégration et des conditions du problème (conditions de Cauchy par exemple). Une solution était définie dans un certain intervalle et cet intervalle d'existence dépendait en général du problème. On s'est donc demandé s'il existait des cas où les solutions admettaient des points singuliers fixes, c'est-à-dire indépendants des conditions du problème. Briot et Bouquet en 1855, attaquent la question sur les équations différentielles (non linéaires) du premier ordre dans le champ complexe. Ils se proposent ainsi de déterminer les équations n'ayant que des pôles mobiles. Ces études se poursuivent avec Émile Picard et Henri Poincaré. Pour les équations différentielles y'=g(y,s)/h(y,s), où g et h sont des polynômes en y sans facteur commun à coefficients holomorphes en s, Painlevé démontre rigoureusement (ce qu'avaient admis Briot et Bouquet) qu'une solution y ne peut pas ne pas avoir de limite, finie ou infinie, quand la variable s tend vers un point a singulier mobile. Autrement dit, une singularité essentielle a ne peut être qu'un point d'indétermination (en y) du rapport de g(y,a) par h(y,a) et de tels points sont fixes et isolés. La solution y(s) tend donc vers une limite qui peut être finie ou infinie quand s tend vers un point singulier mobile a. Si la limite est finie, a est alors un pôle de g/h et un point de branchement de la solution qui est de la forme y(s) = (s − a)1 / (k + 1)u(s) où k est l'ordre du pôle de g/h et u(s) est holomorphe au voisinage de a. On en déduit que les seules équations de cette forme sans point de branchement mobile sont les équations de Riccati à coefficients holomorphes.
La question est d'une tout autre difficulté pour les équations différentielles d'ordre 2. Painlevé en vint à bout en 1899 pour les équations différentielles de la forme y"=f(s,y,y') où f est une fonction rationnelle en y et y' à coefficients holomorphes en s. Il détermine les équations différentielles pour lesquelles il n'y a ni point singulier essentiel mobile ni point de branchement mobile par changements de variable et de fonction dépendant analytiquement d'un paramètre t tels que s = s0 + tnS, y = y0 + tmY, ramenant l'équation à la forme Y"=G(S,Y,Y',t) de façon que pour une valeur t0, par exemple t=0, du paramètre, l'équation puisse être intégrée explicitement. Si l'équation n'a ni point singulier essentiel mobile ni point de branchement mobile pour t différent de t0, il montre qu'il en est de même pour t=t0. Comme on connaît la solution de l'équation pour t0, cela fournit des conditions nécessaires pour que toute intégrale de l'équation initiale n'ait que des pôles mobiles. Par des applications répétées de ce procédé, Painlevé et Gambier parviennent à 50 types d'équations dont 44 sont intégrables explicitement ou dont on connaît une intégrale première. Il reste 6 cas qui ne se traitent pas ainsi. La plus simple est y"=6y²+s dont Painlevé parvint à montrer que ses solutions étaient uniformes n'ayant que des pôles mobiles et qu'elles ne s'exprimaient pas par des fonctions élémentaires ou elliptiques. Ces transcendantes sont depuis appelées transcendantes de Painlevé.
En publiant son mémoire en 1902 dans les Acta mathematica, Painlevé indiqua dans un tableau ses résultats mais il avait oublié un cas qui fut complété par Gambier dans sa thèse soutenue en 1909.
Le calcul opérationnel
Dans les années 1880, un ingénieur anglais, Oliver Heaviside, publie des articles dans lesquels il utilise une méthode de résolution des équations différentielles à la fois originale et injustifiée, même par son auteur qui déclare à ce propos qu'on ne refuse pas un repas parce qu'on n'a pas bien compris le fonctionnement de la digestion ! Sa méthode consiste à utiliser la lettre p à la place de l'opérateur de différentiation d/dt. et à considérer de la même manière que 1/p est l'opérateur d'intégration... Il fait, en fait, du calcul algébrique sur p après avoir traduit la fonction cherchée et revient à l'original à la fin. Tout cela laisse pantois les mathématiciens « sérieux » mais ceux-ci cependant conviennent, sans explication, que la méthode d'Heaviside donne les résultats escomptés. Dans les années 1920, Carson, montre que la méthode d'Heaviside s'explique si l'on considère une transformation intégrale qui consiste à associer à une fonction f(t) sa transformée, la fonction g(p)=Lf(t) définie par

On s'aperçut bientôt que la méthode d'Heaviside avait eu un précurseur, Laplace. De ce fait, la méthode porte aujourd'hui le nom de « transformation de Carson-Laplace » ou seulement « transformation de Laplace ». À sa suite, on utilisera tout une gamme de transformations fonctionnelles, tels que les transformations de Mellin, de Fourier, de Laplace bilatérale (l'intégrale est sur R au lieu d'être sur R+), ... Lesdites transformations sont très étudiées, par Lerch, Carson, Bromwich, ... On démontre ainsi que si l'on connaît la transformée g(p) de Carson-Laplace (unilatérale) d'une fonction f(t), la fonction est donnée par la formule

Des tables de correspondances sont publiées. Van Der Waerden, dans les années 1920, s'en sert en théorie analytique des nombres pour donner une preuve du théorème des nombres premiers,... Pour les besoins de la théorie des équations aux dérivées partielles, un calcul opérationnel à plusieurs variables est inventé.
Les équations aux dérivées partielles
Dans un premier temps, les problèmes qui mènent normalement à une équation aux dérivées partielles sont résolus par des méthodes ad-hoc, le plus souvent géométriques. On n'écrit pas l'équation aux dérivées partielles. On ne s'étonnera donc pas que la première équation aux dérivées partielles n'apparaisse qu'assez tard.
Le premier ordre
La théorie de l'intégration des équations aux dérivées partielles du premier ordre ne date que de 1734[28]. L'idée d'Euler est de ramener ladite intégration à celle des équations différentielles ordinaires. Euler montre qu'une famille de fonctions dépendant de deux paramètres a et b de la forme z=f(x,y,a,b) vérifie une équation aux dérivées partielles du premier ordre en éliminant a et b entre les dérivées partielles
 ,
,  et z. Inversement, une telle équation admet une solution dépendant d'une fonction arbitraire. Il parvient ainsi à intégrer plusieurs équations de ce type.
et z. Inversement, une telle équation admet une solution dépendant d'une fonction arbitraire. Il parvient ainsi à intégrer plusieurs équations de ce type.D'Alembert de son côté[29] fonde ses procédés d'intégration sur deux principes :
- La valeur de la dérivée seconde d'une fonction de deux variables est indépendante de l'ordre des différentiations par rapport à ces variables (théorème dû à Euler mais auquel il faut rajouter des conditions)
- La formation d'une différentielle totale exacte moyennant les deux relations dz = pdx + qdy et F(x,y,z,p,q) = 0 de sorte que l'intégration de cette dernière donne l'intégrale.
Vingt ans après, en 1768-1770, Euler, dans ses Institutiones calculi integralis publie un tome 3 consacré à ces équations où il applique les principes indiqués à un assez grand nombre d'équations mais d'une forme particulière. Clairaut avait, dès 1740, et par analogie avec les équations différentielles ordinaires, rencontré les équations différentielles totales exactes d'une famille de surfaces.
Lagrange, dans un mémoire de 1785[30], résume les connaissances de l'époque sur ces questions. Il ne sait intégrer que 11 types d'équations aux dérivées partielles du premier ordre.
La solution de l'intégration de ces équations allait venir d'un mathématicien peu connu, mort en 1784, Paul Charpit. Son mémoire, présenté en 1784 à l'académie des sciences n'a jamais été publié et est resté longtemps une énigme. On n'en savait que ce que Lacroix en avait écrit, ce qui a fait dire de nombreuses contrevérités, jusqu'à ce qu'on retrouve une copie du mémoire en 1928. Charpit part d'un mémoire de Lagrange de 1772 et écrit ce qu'on appelle aujourd'hui les équations différentielles des caractéristiques. Il continue en indiquant qu'il suffit d'intégrer ces équations, si elles sont résolubles, avec l'équation F(x,y,z,p,q)=0, par rapport aux dérivées p et q. Il obtient ainsi l'intégrale complète en intégrant l'équation aux différentielles totales dz = pdx + qdy. C'est la méthode classique d'intégration des équations aux dérivées partielles du premier ordre qu'on trouve dans les cours d'analyse.
Lagrange ne prendra connaissance du mémoire de Charpit qu'en 1793, ce qui explique que le mémoire de 1785 ne sache intégrer que 11 types d'équations. Ces 11 types sont parfaitement expliqués par Charpit qui les prend pour exemples de sa méthode. Cependant, Charpit n'a pas démontré les théorèmes inverses nécessaires à la rigueur de sa méthode :
- Toute intégrale des caractéristiques définit une solution de l'équation linéaire aux dérivées partielles correspondante.
- Toute intégrale des caractéristiques vérifie la condition d'Euler

Ces théorèmes seront démontrés par Jacobi.
Lagrange, quatre ans après avoir pris connaissance du mémoire de Charpit, en 1797, traite ces questions d'une manière plus compliquée que Charpit dans sa Théorie des fonctions analytiques.
Monge, dans ses Applications de l'analyse à la géométrie, en 1809, montre que les solutions sont des courbes de contact avec son enveloppe d'une surface intégrale et que p et q déterminent les plans tangents à cette surface le long de la courbe.
Les noms de Charpit, Lagrange et Monge sont définitivement associés à ce qui va devenir la méthode des caractéristiques.
En 1815, Pfaff[31] étend la méthode de Charpit et donne la première méthode d'intégration d'une équation aux dérivées partielles d'une seule fonction inconnue à un nombre quelconque de variables indépendantes. Ce procédé sera simplifié successivement par Cauchy en 1819[32] puis par Jacobi en 1836[33].
Jacobi est ainsi à l'origine des méthodes d'intégration, qu'on qualifie de modernes, permettant d'achever l'intégration là où les procédés classiques se heurtaient à des difficultés. Bertrand retrouve en 1852 les bases des considérations de Jacobi, avant que le mémoire posthume de Jacobi ne soit publié. |Bour y apporta des contributions importantes.
Sophus Lie reprit le problème de Jacobi et y apporta une réponse originale mais très compliquée, en introduisant la notion de groupe fonctionnel des intégrales. D'autres recherches sur le même sujet furent faites par Saltykow en 1903, par Stekloff en 1909, Russyan et De Donder en 1910.
La théorie des enveloppes
La théorie des enveloppes des courbes planes a été commencée à la fin du XVIIe siècle par Leibniz et Jean Bernoulli. Elle est complétée principalement par Monge mais apparaît comme un élément essentiel dans la théorie des solutions singulières des équations différentielles d'Euler et Lagrange avait généralisé cette théorie aux enveloppes de famille de surfaces à propos des équations aux dérivées partielles du premier ordre. Il reviendra à Monge une étude plus systématique. Monge définit la courbe caractéristique d'une famille de surfaces à un paramètre a, V(x,y,z,a)=0 par les équations V(x,y,z,a)=0 et
 L'élimination de a entre ces équations donne le lieu des caractéristiques ou surface enveloppe de la famille. Il montre alors que les courbes caractéristiques sont tangentes à une même courbe vérifiant
L'élimination de a entre ces équations donne le lieu des caractéristiques ou surface enveloppe de la famille. Il montre alors que les courbes caractéristiques sont tangentes à une même courbe vérifiant 
Dans son étude sur les applications de l'analyse à la géométrie (1809), Monge montre qu'une surface développable est applicable sur un plan, répondant ainsi à un problème d'Euler et montre que les surfaces développables z=f(x,y) vérifient l'équation rt − s2 = 0.
Ces idées lui permirent de formuler la notion de bande caractéristique et le menèrent à l'intégration de l'équation de Monge-Ampère
rt − s2 + Ar + Bs + ct + D = 0, où A, B, C, D sont des fonctions de x,y,z, p, q.
Les travaux de Monge seront poursuivis pendant tout le XIXe siècle sur les surfaces satisfaisant à des conditions géométriques (surfaces canal, surfaces moulures, surfaces de Weingarten…).
La théorie des surfaces minima
Euler avait défini la notion de ligne géodésique, c'est-à-dire de « lignes de moindre longueur ». Une surface minima généralise à deux dimensions le concept de géodésique en réalisant le minimum de l'aire ayant pour frontière une courbe fermée donnée. C'est Lagrange qui écrivit l'équation aux dérivées partielles des surfaces minima z=f(x,y) en 1760:
(1 + q2)r − 2pqs + (1 + p2)t = 0. Monge tente d'intégrer l'équation en 1784 mais commet des erreurs rectifiées par Legendre en 1787. Legendre y introduit la transformation de Legendre.
La théorie sera complétée par Meusnier, Sophie Germain, Bonnet, Weierstrass, Riemann, Schwarz, Lie et reste encore aujourd'hui un vaste champ d'étude (Nitsche, Ossermann, Chern, Calabi, Bombieri et d'autres).
Les équations aux dérivées partielles d'ordre 2 et plus
En dehors de la géométrie, les équations aux dérivées partielles d'ordre un n'ont que peu de rapport avec les applications de l'analyse. Il en va tout autrement avec les équations d'ordre supérieur qu'on rencontre dès le XVIIIe siècle dans la mécanique des corps déformables, dans l'hydrodynamique, et dans la théorie de l'élasticité. La difficulté est de traduire les lois de la mécanique newtonienne sur des corps non rigides. Les Bernoulli, Taylor, Euler, avant 1740, n'écrivent pas d'équations aux dérivées partielles mais utilisent des raisonnements géométriques particuliers à chaque cas. C'est seulement en 1743 que D'Alembert écrit la première équation aux dérivées partielles de la mécanique, à propos des oscillations d'une chaine pesante au voisinage de sa position d’équilibre :

On rencontre bien vite l'équation

en hydrodynamique puis l'équation des ondes dans la propagation du son

et l'analogue dans la vibration d'une membrane. Laplace rencontre, dans sa théorie des marées, l'équation

et Euler l'équation des vibrations des tiges qui est d'ordre 4:

Pour les applications, il s'agit de résoudre des problèmes avec des conditions aux limites et non trouver les solutions générales de ces équations. Mais les techniques du XVIIIe siècle ne sont pas assez puissantes pour étudier ces équations. Une seule sera étudiée en détail, l'équation des cordes vibrantes la plus simple, l'équation

qui est résolue par D'Alembert, par changement de variable y=x-ct et z=x+ct. Il obtient ainsi l'équation triviale

En revenant aux variables d'origines, il trouve que la solution générale est de la forme u=f(x-ct)+g(x+ct), f et g étant deux fonctions arbitraires.
Mais au XVIIIe siècle, on ne fait pas la distinction entre opérateurs différentiels elliptiques, paraboliques ou hyperboliques. Par contre, on cherche des solutions stationnaires et on utilise pour cela la méthode de séparation des variables.
Notes
- Manifestement, il avait tort. Même à son époque, la question faisait encore travailler : Fields, un jeune mathématicien américain passe sa thèse, en 1887, sur Symbolic finite solutions and solutions by definite integrals of the equation

Références
- A. Dahan-Dalmedico et J. Peiffer, Une Histoire des mathématiques - Routes et dédales [détail des éditions], p 75.
- Karine Chemla, Guo Shuchun, Neuf Chapitres. Le Classique de la Chine ancienne et ses commentaires. Édition critique. [détail des éditions], p144-147
- La première inconnue par l'IREM de Poitiers p 27.
- A. Dahan-Dalmedico et J. Peiffer, Une Histoire des mathématiques - Routes et dédales [détail des éditions], p 76
- Voir par exemple : R. Rashed Entre arithmétique et algèbre : recherches sur l'histoire des mathématiques arabes Paris, Les Belles lettres (1984).
- L. Rodet L’Algèbre d'Al-Khârizmi et les méthodes indienne et grecque lire sur Gallica p 24.
- C. Drouin Muhammad Al-Khâwârîzmî Équipe académique Mathématiques (2001)
- L'exemple est tiré de la même source.
- A. Dahan-Dalmedico et J. Peiffer, Une Histoire des mathématiques - Routes et dédales [détail des éditions], p 85.
- Voir à ce sujet l'article : Algèbre géométrique (mathématiques élémentaires)
- A. Dahan-Dalmedico et J. Peiffer, Une Histoire des mathématiques - Routes et dédales [détail des éditions], p 95
- L'Europe mathématique, dirigé par Catherine Goldstein, Jeremy Gray et Jim Ritter, Éditions de la Maison des sciences de l'homme, Paris, ISBN = 2 7351 0685 3, p. 228
- L'Europe mathématique, dirigé par Catherine Goldstein, Jeremy Gray et Jim Ritter, Éditions de la Maison des sciences de l'homme, Paris, ISBN = 2 7351 0685 3, p. 235
- Lodovico Ferrari Encyclopædia Britannica
- Daniel Boorstin, Les Découvreurs, Éditions Stegers, 1983, pp. 57-79
- L'Europe mathématique, dirigé par Catherine Goldstein, Jeremy Gray et Jim Ritter, Éditions de la Maison des sciences de l'homme, Paris, ISBN = 2 7351 0685 3, p. 241
- Picard, Sur les groupes de transformation des équations différentielles linéaires, CRAS T96, 1883, p1131.
- Picard, Sur les équations différentielles linéaires et les groupes algébriques de transformation, Annales de la faculté des sciences de Toulouse, T1, 1887
- Vessiot, Sur l'intégration des équations différentielles linéaires, Gauthier-Villars, Paris, 1892
- Vessiot, thèse, p45
- Vessiot, Thèse, p46
- Vessiot, thèse, p49
- Liouville, Sur l'intégration d'une classe d'équations différentielles du second ordre en quantités finies explicites, Journal de mathématiques pures et appliquées, T4, 1839, p423
- Painlevé, Le problème moderne de l'intégration des équations différentielles, Bulletin des sciences mathématiques, T28, 1904, p193-208
- Ore, The theory of non-commutative polynomials. Annals of Mathematics, T34, 1933, p480-508
- Fuchs, Zur theorie der linearen differentialgleichungen mit veränderlichen coefficienten, Journal für die reine und angewandte mathematik,T66, 1866, p121-160.
- Decuyper, Modèles mathématiques de la physique, Dunod, 1968, chapitre 3
- Euler, De infinitis curvis eiusdem generis seu methodus inveniendi aequationes pro infinitis curvis eiusdem generis, Commentarii academiae scientiarvm imperialis petropolitanae, T7, 1740, p174-193
- Sur la courbe que forme une corde tendue mise en vibration, Histoire de l'académie de Berlin, 1747, tome 3, p14-49
- Lagrange, Méthode générale pour intégrer les équations aux différences partielles du premier ordre, lorsque ces différences ne sont que linéaires, Nouveaux mémoires de l'académie des sciences et belles-lettres de Berlin, 1785
- Allgemeine methode partielle differentialgleichungen und gewöhnliche differentialgleichungen, beide von ester ordnung, in beliebig vielen veränderlichen, vollständig zu integriren, Abhandlungen der Königlichens akademie den wissenchaften in Berlin, 1814-1815
- Bulletin de la société philomatique de Paris, 1819, p10
- Jacobi, Ueber die reduction der integration der partiellen differentialgleichungen erster ordnung zwischen irgend einer zahl variabeln auf die integration eines einzigen systems gewöhnlicher differentialgleichungen, Gesammelte Werke, bd IV, p59
Voir aussi
Bibliographie
- Galle, Mathematische instrumente, Teubner, Leipzig & Berlin, 1912.
- Horsburgh & al, Modern instruments and methods of calculation, Bells & sons, Londres, 1914.
- De Morin, Les appareils d'intégration, Gauthier-Villars, Paris, 1913.
Wikimedia Foundation. 2010.
