- James Stirling (mathematicien)
-
James Stirling (mathématicien)
James Stirling (mai 1692[1],[2] à Garden près de Stirling – 5 décembre 1770 à Leadhills) est un mathématicien écossais.
Biographie et contributions
Stirling a été découvert par Newton. En 1717, il enseigna à Venise et publia ses premiers travaux à Rome, Lineae Tertii Ordinis Neutonianae, qui développent la théorie de Newton sur les courbes planes de degré 3, ajoutant un nouveau niveau de courbes aux 72 donnés par Newton. Ses travaux furent publiés à Oxford et Newton lui-même en reçut une copie.
Lineae Tertii Ordinis Neutonianae contient d'autres résultats que Stirling avait obtenus. Ce sont des résultats sur les courbes à descente rapide, sur les enchaînements (en particulier, ces problèmes sont relatifs au placement de sphères dans une voûte), et sur les trajectoires orthogonales. Le problème des trajectoires orthogonales a été soulevé par Leibniz et de nombreux mathématiciens autres que Stirling travaillèrent sur le problème, ainsi Jean Bernoulli, Nicolas Bernoulli I, Nicolas Bernoulli II et Leonhard Euler. On sait que Stirling résolut ce problème au début de 1716.
À Londres, Stirling publia ses principaux travaux Methodus Differentialis en 1730. Ce livre porte sur les séries infinies, l'addition, la somme, l'interpolation et les puissances carrées. À cette époque, Stirling était en correspondance avec de Moivre, Cramer et Euler.
L'équivalent asymptotique de n!, pour lequel Stirling est le plus connu, apparaît à l'Exemple 2 de la Proposition 28 de Methodus Differentialis. Un des principaux objectifs de cet ouvrage était d'étudier des méthodes pour accélérer la convergence des séries. Stirling note d'ailleurs dans sa préface que Newton avait étudié ce problème. Beaucoup d'exemples de ses méthodes sont donnés, dont le problème de Leibniz de π / 4 = 1 − 1 / 3 + 1 / 4 − 1 / 5 + 1 / 6 − ... Il applique également ses procédés d'accélération à la somme de la série 1 + 1 / 4 + 1 / 9 + 1 / 16 + ... dont la valeur exacte était encore inconnue à l'époque. Il obtient (Prop.11, exemple 1) la relation
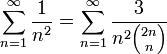qui lui permet d'obtenir la valeur approchée 1.64493406684822643, mais ne reconnaît pas π2 / 6, ce qui sera fait par Euler peu d'années après.Il donne également un théorème à propos de la convergence d'un produit infini. Dans ses travaux sur l'accélération de la convergence des séries se trouve une discussion des méthodes de de Moivre. L'ouvrage contient d'autres résultats sur la fonction Gamma d'Euler et la fonction hypergéometrique.
Notes et références
- ↑ Algebraic number theory,Richard A. Mollin
- ↑ Bibmath.net
Voir aussi
Portail des mathématiques
Portail de l’Écosse
Catégories : Mathématicien écossais | Naissance en 1692 | Décès en 1770
Wikimedia Foundation. 2010.
