Theoreme de la moyenne

Theoreme de la moyenne

Théorème de la moyenne

En analyse réelle, le théorème de la moyenne est un résultat classique concernant l'intégration des fonctions continues d'une variable réelle. La moyenne d'une fonction continue sur un segment se réalise comme valeur de la fonction. Plus précisément :

Énoncé — Pour toute fonction d'une variable réelle f définie et continue sur un segment [a,b], avec a<b, il existe un réel c strictement compris entre a et b vérifiant :

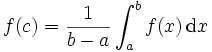f(c)=\frac{1}{b-a}\int_a^b f(x)\, \mathrm{d}x .

L'intégrale est ici définie soit au sens de Riemann, soit au sens de Lebesgue.

Graphiquement, une interprétation de ce théorème est que l'aire algébrique sous la courbe représentative de f est égale à celle d'un rectangle de base [a,b], et de hauteur un point moyen de la courbe. On peut démontrer le théorème de la moyenne à partir du théorème des accroissements finis.

Ce théorème s'étend aux fonctions réelles de plusieurs variables sur un domaine compact et connexe par les intégrales multiples.

Sommaire

Errata

  • Le point c ne dépend pas continûment de f. Le théorème de la moyenne, comme conséquence du théorème des accroissements finis, pose l'existence d'un réel c mais ne donne aucune information sur sa dépendance en la fonction f.
  • L'hypothèse de continuité est essentielle. Le résultat devient trivialement faux pour une fonction mesurable mais non continue (où l'intégrale serait définie au sens de Lebesgue).

Preuves

Preuve par l'absurde

Supposons par l'absurde que la moyenne de f n'est pas réalisé comme valeur de f :

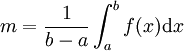m=\frac{1}{b-a}\int_a^bf(x)\mathrm dx.

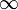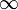Comme l'image du segment [a,b] par f est connexe par arcs (théorème des valeurs intermédiaires), l'image de f est un fermé contenu soit dans (-\infty,m), soit dans (m,+\infty) :

  • Dans le premier cas, le maximum de f est strictement inférieur à m, disons égal à m-r avec r>0, et il vient :
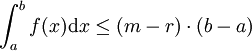    \int_a^bf(x)\mathrm dx\leq (m-r)\cdot(b-a) ;

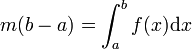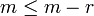Comme m(b-a)=\int_a^bf(x)\mathrm dx , on obtient la contradiction suivante: m \leq m-r .

  • Dans le second cas, le minimum de f est strictement supérieur à m, disons égal à m+r avec r>0, et il vient :
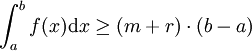    \int_a^bf(x)\mathrm dx\geq (m+r)\cdot(b-a).

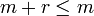De la même manière, on en déduit la contradiciton m +r \leq m .

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de la moyenne ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de la moyenne de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Théorème de la moyenne — En analyse réelle, le théorème de la moyenne est un résultat classique concernant l intégration des fonctions continues d une variable réelle, selon lequel la moyenne d une fonction continue sur un segment se réalise comme valeur de la fonction.… …   Wikipédia en Français

  • théorème de la moyenne — vidutinės vertės teorema statusas T sritis fizika atitikmenys: angl. mean value theorem vok. Mittelwertsatz, m rus. теорема о среднем значении, f pranc. théorème de la moyenne, m …   Fizikos terminų žodynas

  • Theoreme de la moyenne de Cauchy — Théorème de la moyenne de Cauchy Pour les articles homonymes, voir Cauchy. Soient f et g deux fonctions continues sur [a,b] et différentiables sur ]a,b[. Si la dérivée g ne s annule pas sur ]a,b[, alors il existe . Ce théorème permet de démontrer …   Wikipédia en Français

  • Théorème de la moyenne de Cauchy — Pour les articles homonymes, voir Cauchy. Soient f et g deux fonctions continues sur [a,b] et différentiables sur ]a,b[. Si la dérivée g ne s annule pas sur ]a,b[, alors il existe . Ce théorème permet de démontrer la règle de l Hôpital …   Wikipédia en Français

  • Théorème de la moyenne de cauchy — Pour les articles homonymes, voir Cauchy. Soient f et g deux fonctions continues sur [a,b] et différentiables sur ]a,b[. Si la dérivée g ne s annule pas sur ]a,b[, alors il existe . Ce théorème permet de démontrer la règle de l Hôpital …   Wikipédia en Français

  • Théorème de WICK — Le théorème de Wick est un outil particulièrement important de la physique statistique, dans la mesure où il permet de calculer des valeurs moyennes d observables compliquées, par exemple des corrélations ou des interactions à plusieurs… …   Wikipédia en Français

  • Théorème de wick — Le théorème de Wick est un outil particulièrement important de la physique statistique, dans la mesure où il permet de calculer des valeurs moyennes d observables compliquées, par exemple des corrélations ou des interactions à plusieurs… …   Wikipédia en Français

  • Theoreme des accroissements finis — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Théorème des accroissements finis généralisé — Théorème des accroissements finis En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d une variable réelle, son accroissement entre deux valeurs est réalisable comme… …   Wikipédia en Français

  • Théorème de Wick — Le théorème de Wick est un outil particulièrement important de la physique statistique, dans la mesure où il permet de calculer des valeurs moyennes d observables compliquées, par exemple des corrélations ou des interactions à plusieurs… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”