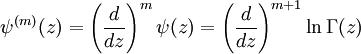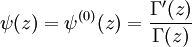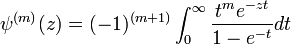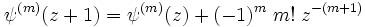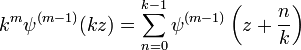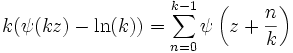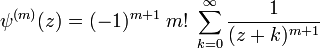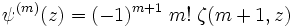Fonction Polygamma

Fonction polygamma

Tracé de la fonction polygamma le long de l'axe des réels avec en orange m=0, en jaune m=1, en vert m=2, en rouge m=3 et en bleu m=4

En mathématiques, la fonction polygamma d'ordre m est définie comme la m+1 -ième dérivée logarithmique de la fonction gamma :

$\psi^{(m)}(z) = \left(\frac{d}{dz}\right)^m \psi(z) = \left(\frac{d}{dz}\right)^{m+1} \ln\Gamma(z)$

Ici,

$\psi(z) =\psi^{(0)}(z) = \frac{\Gamma'(z)}{\Gamma(z)}\,$

est la fonction digamma et 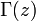$\Gamma(z)\,$ est la fonction gamma. On appelle aussi parfois la fonction 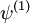$\psi^{(1)}\,$ fonction trigamma.

Définition par intégrale

La fonction polygamma peut être représenté par:

$\psi^{(m)}(z)= (-1)^{(m+1)}\int_0^\infty \frac{t^m e^{-zt}} {1-e^{-t}} dt$

Ceci n'est valable que pour Re z > 0 et m > 0. Pour m = 0, voir la définition de la fonction digamma.

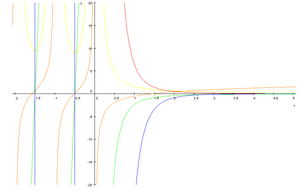
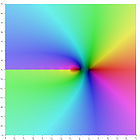
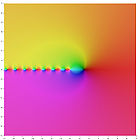
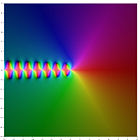
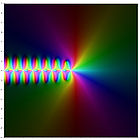
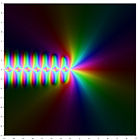
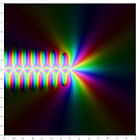
Représentation dans le plan complexe

**La représentation du logarithme de la fonction gamma et des premiers ordres de la fonction polygamma dans le plan complexe est:**

$lnΓ(z)$	$ψ (0) (z)$	$ψ (1) (z)$	$ψ (2) (z)$	$ψ (3) (z)$	$ψ (4) (z)$

Relation de récurence

Elle possède la relation de récurrence

$\psi^{(m)}(z+1)= \psi^{(m)}(z) + (-1)^m\; m!\; z^{-(m+1)}\,$

Théorème de multiplication

Le théorème de multiplication donne:

$k^{m} \psi^{(m-1)}(kz) = \sum_{n=0}^{k-1} \psi^{(m-1)}\left(z+\frac{n}{k}\right)$

Valable pour $m > 1$ , et, pour $m = 0$ la formule de multiplication de la fonction digamma est:

$k (\psi(kz)-\ln(k)) = \sum_{n=0}^{k-1} \psi\left(z+\frac{n}{k}\right)$

Représentation par série

La fonction polygamma a pour représentation en série:

$\psi^{(m)}(z) = (-1)^{m+1}\; m!\; \sum_{k=0}^\infty \frac{1}{(z+k)^{m+1}}$

Qui n'est valable que pour m > 0 et pour tout complexe z qui n'est pas égale à un nombre entier négatif. Cette représentation peut être écrite avec la fonction zêta d'Hurwitz par

$\psi^{(m)}(z) = (-1)^{m+1}\; m!\; \zeta (m+1,z)\,$

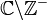On peut en conclure que la fonction zêta d'Hurwitz généralise la fonction polygamma à n'importe quel ordre appartenant à $\mathbb C \backslash \mathbb Z^-$ .

Série de Taylor

La série de Taylor au point z=1 est

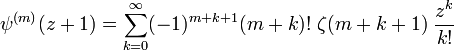$\psi^{(m)}(z+1)= \sum_{k=0}^\infty (-1)^{m+k+1} (m+k)!\; \zeta (m+k+1)\; \frac {z^k}{k!}\,$ ,

qui converge pour |z|<1. Ici, 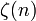$\zeta(n)\,$ est la fonction zêta de Riemann.

Références

Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4 . Voir la section 6.4.

Portail des mathématiques

Ce document provient de « Fonction polygamma ».

Catégories : Fonction gamma ou associée | Fonctions spéciales

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction Polygamma de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Fonction polygamma — Tracé de la fonction polygamma le long de l axe des réels avec en orange m=0, en jaune m=1, en vert m=2, en rouge m=3 et en bleu m=4 En mathématiques, la fonction polygamma d ordre m est définie comme la m+1 ième dérivée logarithmique de la… … Wikipédia en Français
Fonction Gamma — Pour les articles homonymes, voir gamma (homonymie). Tracé de la fonction gamma le long de l axe des réels En mathématiques, la fonction g … Wikipédia en Français
Fonction Gamma d'Euler — Fonction gamma Pour les articles homonymes, voir gamma (homonymie). Tracé de la fonction gamma le long de l axe des réels En mathématiques, la fonction g … Wikipédia en Français
Fonction Zeta D'Hurwitz — Fonction zêta d Hurwitz En mathématiques, la fonction zêta d Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit : . Elle s étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre… … Wikipédia en Français
Fonction Zeta d'Hurwitz — Fonction zêta d Hurwitz En mathématiques, la fonction zêta d Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit : . Elle s étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre… … Wikipédia en Français
Fonction zeta d'Hurwitz — Fonction zêta d Hurwitz En mathématiques, la fonction zêta d Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit : . Elle s étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre… … Wikipédia en Français
Fonction zeta d'hurwitz — Fonction zêta d Hurwitz En mathématiques, la fonction zêta d Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit : . Elle s étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre… … Wikipédia en Français
Fonction zêta d'Hurwitz — En mathématiques, la fonction zêta d Hurwitz est une des nombreuses fonctions zêta. Elle est définie comme suit : . Elle s étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre complexe q qui n est pas… … Wikipédia en Français
Fonction Beta De Dirichlet — Fonction bêta de Dirichlet En mathématiques, la fonction β de Dirichlet, aussi appelée fonction ζ de Catalan, est un des exemples les plus simples de fonction L, après la fonction zêta de Riemann. C est un cas particulier de fonction L de… … Wikipédia en Français
Fonction beta de Dirichlet — Fonction bêta de Dirichlet En mathématiques, la fonction β de Dirichlet, aussi appelée fonction ζ de Catalan, est un des exemples les plus simples de fonction L, après la fonction zêta de Riemann. C est un cas particulier de fonction L de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction Polygamma