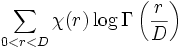Formule De Chowla-Selberg
- Formule De Chowla-Selberg
-
Formule de Chowla-Selberg
En mathématiques, la formule de Chowla-Selberg est l'évaluation d'un certain produit de valeurs de la fonction gamma aux valeurs rationnelles. Le nom provient d'un papier commun de 1967 des mathématiciens Chowla et Selberg. Le résultat de base était déjà connu plus tôt dans un travail du mathématicien tchèque Mathias Lerch (1860-1922).
Sous une forme logarithmique, la formule montre que dans certains cas, la somme
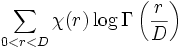
peut être évaluée (par la théorie des formes modulaires). Ici χ est le symbole de Jacobi modulo D, où -D est le discriminant d'un corps quadratique imaginaire. La somme est prise sur 0 < r < D, avec la convention usuelle χ(r) = 0 si r et D ont un facteur commun.
L'origine de ce genre de formules est maintenant perçue dans la théorie de la multiplication complexe, et en particulier dans la théorie des périodes d'une variété abélienne de type CM. Ceci a conduit à beaucoup de recherches et de généralisations. En particulier, à l'analogue des nombres p-adiques, impliquant une fonction gamma p-adique, qui a été initiée par Gross et Koblitz, une notion importante dans la théorie des périodes p-adiques.
 Portail des mathématiques
Portail des mathématiques
Catégorie : Théorie analytique des nombres
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Formule De Chowla-Selberg de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Formule de chowla-selberg — En mathématiques, la formule de Chowla Selberg est l évaluation d un certain produit de valeurs de la fonction gamma aux valeurs rationnelles. Le nom provient d un papier commun de 1967 des mathématiciens Chowla et Selberg. Le résultat de base… … Wikipédia en Français
Formule de Chowla-Selberg — En mathématiques, la formule de Chowla Selberg est l évaluation d un certain produit de valeurs de la fonction gamma aux valeurs rationnelles. Le nom provient d un papier commun de 1967 des mathématiciens Chowla et Selberg. Le résultat de base… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 … Wikipédia en Français
Liste des matieres de la theorie des nombres — Liste des matières de la théorie des nombres Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 … Wikipédia en Français
Liste des matières de la théorie des nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 Test de primalité e … Wikipédia en Français
Fonction Gamma — Pour les articles homonymes, voir gamma (homonymie). Tracé de la fonction gamma le long de l axe des réels En mathématiques, la fonction g … Wikipédia en Français
Fonction Gamma d'Euler — Fonction gamma Pour les articles homonymes, voir gamma (homonymie). Tracé de la fonction gamma le long de l axe des réels En mathématiques, la fonction g … Wikipédia en Français
Fonction gamma — Pour les articles homonymes, voir gamma (homonymie). Tracé de la fonction gamma le long de l axe des réels En mathématiques, la fonction gamma (ou fonction Gamma) est une fonction … Wikipédia en Français