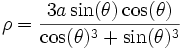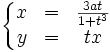Foliums
- Foliums
-
Folium de Descartes

Le Folium de Descartes
Étymologie et histoire
Le Folium de Descartes est une courbe mathématique étudiée tout d'abord par Descartes et Roberval en 1638 (lors d'une correspondance avec Mersenne) puis étudiée par Huygens en 1672. Cette courbe met en évidence les faiblesses de la méthode de Fermat dans la recherche des extremums d'une courbe algébrique.
La courbe possède une forme de nœud de ruban. Lors de leur étude, Descartes et Roberval se limitèrent à une boucle, ne considérant que les coordonnées positives (x>0,y>0) car ils pensaient que la boucle se répetait dans chaque quart de repère, à la manière des quatre pétales d'une fleur (d'où son nom de folium = feuille). La méthode de détermination des tangentes à la courbe fut ensuite proposée par Roberval. La nature asymptotique des branches infinies ne fut établie qu'en 1692 par Huygens.
Définition mathématique
Le folium de Descartes n'est en général pas défini par une propriété géométrique, c'est une cubique définie par :
- x3 + y3 = 3axy
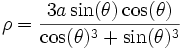
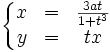
a étant un réel quelconque.
L'aire de la boucle est égale à celle du domaine situé entre la courbe et son asymptote (d'équation x + y = − a) de valeur 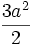 et cette courbe admet l'origine comme point double.
et cette courbe admet l'origine comme point double.
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Foliums de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Foliums — Folium Fo li*um, n.; pl. E. {Foliums}, L. {Folia}. [L., a leaf.] 1. A leaf, esp. a thin leaf or plate. [1913 Webster] 2. (Geom.) A curve of the third order, consisting of two infinite branches, which have a common asymptote. The curve has a… … The Collaborative International Dictionary of English
Folia — Folium Fo li*um, n.; pl. E. {Foliums}, L. {Folia}. [L., a leaf.] 1. A leaf, esp. a thin leaf or plate. [1913 Webster] 2. (Geom.) A curve of the third order, consisting of two infinite branches, which have a common asymptote. The curve has a… … The Collaborative International Dictionary of English
Folium — Fo li*um, n.; pl. E. {Foliums}, L. {Folia}. [L., a leaf.] 1. A leaf, esp. a thin leaf or plate. [1913 Webster] 2. (Geom.) A curve of the third order, consisting of two infinite branches, which have a common asymptote. The curve has a double point … The Collaborative International Dictionary of English
Quadriques rationnelles non-bicirculaires — Les quadriques rationnelles non bicirculaires sont une famille de courbes algébriques de degré 4, de genre 0 et non bicirculaires[Quoi ?]. On peut citer : Les conchoïdes de Nicomède Les cruciformes (liés à l ellipse) ou les pontiformes… … Wikipédia en Français
folium — [fō′lē əm] n. pl. foliums or folia [fō′lēə] [L: see FOLIATE] 1. Geol. a thin layer of stratum, as in metamorphic rock 2. Geom. the looping, closed part of a curve extending from a node … English World dictionary
 Le Folium de Descartes
Le Folium de Descartes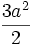 et cette courbe admet l'origine comme point double.
et cette courbe admet l'origine comme point double.