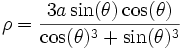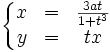Folium de descartes
- Folium de descartes
-
Folium de Descartes

Le Folium de Descartes
Étymologie et histoire
Le Folium de Descartes est une courbe mathématique étudiée tout d'abord par Descartes et Roberval en 1638 (lors d'une correspondance avec Mersenne) puis étudiée par Huygens en 1672. Cette courbe met en évidence les faiblesses de la méthode de Fermat dans la recherche des extremums d'une courbe algébrique.
La courbe possède une forme de nœud de ruban. Lors de leur étude, Descartes et Roberval se limitèrent à une boucle, ne considérant que les coordonnées positives (x>0,y>0) car ils pensaient que la boucle se répetait dans chaque quart de repère, à la manière des quatre pétales d'une fleur (d'où son nom de folium = feuille). La méthode de détermination des tangentes à la courbe fut ensuite proposée par Roberval. La nature asymptotique des branches infinies ne fut établie qu'en 1692 par Huygens.
Définition mathématique
Le folium de Descartes n'est en général pas défini par une propriété géométrique, c'est une cubique définie par :
- x3 + y3 = 3axy
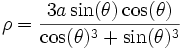
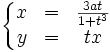
a étant un réel quelconque.
L'aire de la boucle est égale à celle du domaine situé entre la courbe et son asymptote (d'équation x + y = − a) de valeur 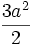 et cette courbe admet l'origine comme point double.
et cette courbe admet l'origine comme point double.
 Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Folium de descartes de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Folium de Descartes — Saltar a navegación, búsqueda Folium de Descartes x3 + y3 − 3axy = 0,a = 1 El folium de Descartes (‘hoja de Descartes’) es una curva algebraica propuesta por vez primera por Descartes en 1638 con la ecuación implícita: x … Wikipedia Español
Folium De Descartes — Le Folium de Descartes Étymologie et histoire Le Folium de Descartes est une courbe mathématique étudiée tout d abord par Descartes et Roberval en 1638 (lors d une correspondance avec Mersenne) puis étudiée par Huygens en 1672. Cette courbe met… … Wikipédia en Français
Folium von Descartes — Folium von Descartes, s. Descartessches Blatt … Lexikon der gesamten Technik
Folium de Descartes — Le folium de Descartes (en vert) et son asymptote (en bleu) pour a=1. Le folium de Descartes est une courbe algébrique mathématique une forme de nœud de ruban. Étymologie et histoire Elle fut étudiée tout d abord par Descartes et Roberval en 1638 … Wikipédia en Français
Folium of Descartes — In Geometry, the Folium of Descartes is an algebraic curve defined by the equation :x^3 + y^3 3 a x y = 0 ,. It forms a loop in the first quadrant with a double point at the origin and asymptote :x + y + a = 0 ,. It is symmetrical about y =… … Wikipedia
Folium — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Folium peut faire référence à: une feuille d arbre une feuille de papier Folium de Descartes, une courbe mathématique folium de Dürer, une courbe Sextique … Wikipédia en Français
Folium Cartesii — (Foliata curva, lat.), eine von Descartes zuerst angegebene krumme Linie von Blattform, deren Gleichung ist x3 + y2 =axy. Sie hat 2 Zweige mit einer geradlinichten Asymptote, an der diese auf derselben Seite sich erstrecken. Unter Newtons Linien… … Pierer's Universal-Lexikon
René Descartes — Descartes redirects here. For other uses, see Descartes (disambiguation). René Descartes Portrait after Frans Ha … Wikipedia
Théories scientifiques de Descartes — René Descartes a élaboré de nombreuses théories scientifiques. Chez lui, la science n est pas séparable de la philosophie. Science et philosophie agissent constamment l une sur l autre dans la pensée cartésienne, puisque sa méthode vise à… … Wikipédia en Français
Foliums — Folium de Descartes Le Folium de Descartes Étymologie et histoire Le Folium de Descartes est une courbe mathématique étudiée tout d abord par Descartes et Roberval en 1638 (lors d une correspondance avec Mersenne) puis étudiée par Huygens en 1672 … Wikipédia en Français
 Le Folium de Descartes
Le Folium de Descartes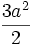 et cette courbe admet l'origine comme point double.
et cette courbe admet l'origine comme point double.