Adjoint d'un endomorphisme

Adjoint d'un endomorphisme

Opérateur adjoint

En mathématiques l'adjoint d'un opérateur, quand il existe, est un nouvel opérateur défini sur un espace vectoriel sur le corps des nombres réels ou complexes et munis d'un produit scalaire. Un tel espace est qualifié de préhilbertien.

Si l'opérateur initial est continu et si l'espace vectoriel est complet l'adjoint est toujours défini. Cette configuration se produit toujours en dimension finie. L'application qui, à un opérateur associe son adjoint, est linéaire continue bijective. Cette fonction est même une isométrie involutive. L'espace des opérateurs se décompose en deux sous-espaces vectoriels supplémentaires orthogonaux. Ce sont des espaces propres de l'application associés aux valeurs propres 1 et -1.

Certains opérateurs disposent d'une compatibilité vis à vis du produit scalaire. Tel est le cas si un opérateur commute avec son adjoint. Il est alors dit normal. Trois cas sont importants, les autoadjoints (resp. antisymétriques) correspondant à un opérateur adjoint de lui-même (resp. dont l'adjoint est son opposé) et orthogonaux dont l'adjoint est l'inverse. Sur un espace vectoriel complexe, le terme utilisé est unitaire et non plus orthogonal.

La notion d'adjoint d'un opérateur possède de nombreuses applications. En dimension finie et sur le corps des nombres complexes, la structure des endomorphismes normaux est simple, ils sont diagonalisables dans une base orthonormale. Le cas de la dimension infinie est plus complexe. Il est important en analyse fonctionnelle. Le cas autoadjoint est particulièrement étudié, il fournit le cadre le plus simple de la théorie spectrale. En algèbre générale, une algèbre stellaire correspond à une structure abstraite d'espace vectoriel munis d'une loi de composition interne analogue à la composition des opérateurs et d'une opération étoile ayant les mêmes propriétés que l'application qui, à un opérateur associe son adjoint.

Sommaire

Définitions

L'adjoint d'un opérateur est une notion correspondant à des situations fort différentes. Elle peut être appliquée dans le cas d'un espace euclidien ou hermitien, c'est-à-dire en dimension finie. Elle est aussi utilisée dans le contexte le plus simple de l'analyse fonctionnelle, c'est-à-dire dans un espace de Hilbert ou un préhilbertien. Elle peut enfin s'appliquer dans un cadre très général sur des espaces de Banach. Pour cette raison deux définitions se côtoient.

Préhilbertien

Cette définition couvre dans la pratique deux cadres théoriques un peu différents. Celui de la dimension finie et celui où aucune hypothèse est faite sur la dimension. Il correspond aussi à un premier cas d'analyse fonctionnelle, le plus simple. En général l'espace vectoriel choisi est un Hilbert, c'est-à-dire que la topologie associée à la distance est complète. Comme il est relativement facile de compléter un préhilbertien et que les théorèmes dont on disposent sont beaucoup plus nombreux, ce cadre est largement utilisé. Une unique définition permet de couvrir des deux cas :

Soit H un espace préhilbertien sur un corps K égal à celui des réels R ou des complexes C. Le produit scalaire est noté (.,.) dans cet article. Soit a et a* deux opérateurs de E.

  • Définition : L'opérateur a* est dit adjoint de a si et seulement si la propriété suivante est vérifiée :
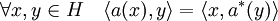
\forall x, y \in H \quad \langle a(x),y\rangle = \langle x,a^*(y)\rangle

Il est d'usage de noter avec le signe * l'adjoint d'un opérateur[1]. Le terme d'opérateur est en général celui utilisé pour désigner une application linéaire.

Algèbre stellaire

Article détaillé : Algèbre stellaire.

Comme la suite de l'article le montre l'application *, qui à un endomorphisme associe son adjoint est une application linéaire de l'espace des endomorphismes. Cet espace dispose, avec la composition des endomorphismes d'une structure d'algèbre. Une application *, disposant des mêmes caractéristiques que l'application adjointe et définie sur une algèbre est le cadre d'une structure appelée algèbre stellaire. L'image d'un élément a par l'application * est appelé adjoint de a[2].

Banach

En analyse fonctionnelle, tous les espaces ne disposent pas d'un produit scalaire. L'approche par les adjoints reste néanmoins fructueuse. L' opérateur a dispose de propriétés plus pauvres que celles du paragraphe précédent.

Dans le cas général, il n'est plus borné, c'est-à-dire qu'il n'existe pas nécessairement de majorant de la norme de l'image d'un vecteur de la boule unité. Ainsi la dérivée d'une fonction de la variable réelle dans l'ensemble réelle à support compact, infiniment différentiable et majorée en valeur absolue par un n'est pas majorée par une constante indépendante de la fonction. Cet espace muni de la norme de la convergence uniforme est important pour la définition des distributions. La dérivée est un opérateur linéaire non borné qui joue un grand rôle en analyse fonctionnelle.

Un opérateur a n'est pas nécessairement défini sur tout le Banach. Ainsi la fonction dérivée n'est pas définie sur toute fonction de ]-1/2, 1/2[ dans R et intégrable en valeur absolue. Pour la même raison que celle du paragraphe précédent, il est néanmoins utile de considérer cet opérateur.

Dans ce paragraphe, E et F désigne deux Banach, a un opérateur non borné de E dans F, E* et F* désignent les duaux topologiques de E et F. Dans la suite de l'article le terme dual signifie dual topologique. Il est en effet plus utilisé que le dual algébrique dans ce contexte. Le terme D(a) désigne le domaine de a, c'est-à-dire le sous-espace vectoriel sur lequel a est défini. Il est supposé dense dans E. La notation <.,.>E (resp. <.,.>F) désigne le crochet de dualité, il correspond à l'application bilinéaire de E*xE (resp. F*xF) qui à un couple formé d'une forme linéaire et d'un vecteur de E (resp. F) associe un scalaire.

  • Définition : Le domaine noté D(a*) de l'opérateur adjoint de a est le sous-ensemble de F* suivant :
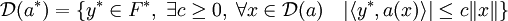
\mathcal{D}(a^*) = \{y^* \in F^*,\; \exists c \ge 0,\; \forall x \in \mathcal{D}(a) \quad |\langle y^*,a(x)\rangle |\le c\|x\|\}

Cette définition permet la suivante :

  • Définition : l'opérateur adjoint a* de a est l'opérateur de D(a*) dans E* vérifiant l'égalité :
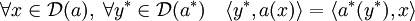
\forall x \in \mathcal{D}(a),\; \forall y^* \in \mathcal{D}(a^*) \quad \langle y^*, a(x)\rangle =\langle a^*(y^*),x\rangle

Il est fréquent que E et F soit confondu, l'adjoint est alors un opérateur de E*.[3]

Espace de Hilbert

Un espace de Hilbert est un cas particulier de préhilbertien. Dans ce cas, le dual topologique s'identifie avec l'espace H. Les résultats obtenus dans le cas des formes bilinéaires s'appliquent sans beaucoup de modifications.

Le cas de la dimension finie est un peu plus simple car toute application linéaire est continue et l'isomorphisme entre l'espace et son dual est plus évident. Une approche plus didactique est disponible dans l'article Espace euclidien pour le cas réel et Espace hermitien pour le cas complexe.

Existence

Un premier cadre de la théorie est celui ou l'espace vectoriel H est muni d'un produit scalaire définissant une norme lui conférant le statut d'espace complet.

  • Tout opérateur sur H admet un adjoint.

En effet, notons (.|.) le produit scalaire de H et a un opérateur borné. Soit y un vecteur de H, l'application qui à un vecteur x associe (a(x)|y) est une forme linéaire. Le théorème de représentation de Riesz garantit l'existence d'un vecteur z tel que l'application qui à x associe (x|z) est égal à la forme linéaire précédente. L'application a* qui à y associe z est par définition l'adjoint de a.

En dimension finie, l'existence d'un tel z se démontre plus aisément. Il suffit de remarquer que l'application qui à un vecteur x associe (x|y) est un isomorphisme de H vers son dual. Elle est en effet injective et l'égalité des dimensions de H et de son dual montre la surjectivité.

Remarque : Dans le cas où le corps sous-jacent à H est celui des complexes, le produit scalaire est sesquilinéaire. La convention choisie dans l'article est que la forme est linéaire pour la première variable et antilinéaire pour la seconde. Le conjugué d'un scalaire λ est noté 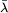\scriptstyle {\bar \lambda} dans cet article. Par défaut, les énoncés sont donnés pour les espaces complexes. Ils restent vrais pour les réels et l'application conjugué devient l'identité.

Propriétés élémentaires

A beaucoup d'égard l'adjoint est une image miroir de l'opérateur.

  • L'adjoint de l'opérateur a est linéaire.

Ce résultat est la conséquence directe des propriétés de linéarité du produit scalaire. Il utilise le fait que  :

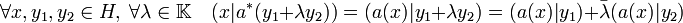
\forall x,y_1,y_2 \in H,\;\forall \lambda \in \mathbb K \quad (x|a^*(y_1+\lambda y_2))= (a(x)|y_1+\lambda y_2)=(a(x)|y_1)+\bar \lambda(a(x)|y_2)

On en déduit :

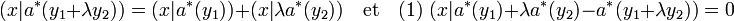
(x|a^*(y_1+\lambda y_2))=(x|a^*(y_1))+(x|\lambda a^*(y_2))\quad \text{et}\quad (1)\; (x|a^*(y_1)+\lambda a^*(y_2)- a^*(y_1+\lambda y_2))=0\;

L'égalité (1) est vraie pour toutes les valeurs de x ce qui montre que le terme de droite est nul. Cette nullité démontre le caractère linéaire de a*.

En dimension finie, la matrice de l'adjoint est égal à la transposée de la matrice conjuguée de a. La démonstration est une fois encore simple, soit A la matrice de a dans une base de H et X (resp. Y) la matrice d'un vecteur x (resp. y) de H.

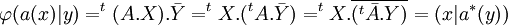
\varphi (a(x)|y)= ^t(A.X).\bar Y= ^tX.(^tA.\bar Y) = ^tX.\overline {(^t \bar A. Y)}= (x|a^*(y))
  • Si l'opérateur a est borné, alors l'adjoint l'est aussi et la norme de a au sens des opérateurs est celle de l'adjoint.

Le terme borné signifie ici que l'image de la boule unité est bornée. Un opérateur est borné si et seulement s'il est continu.

Pour s'en rendre compte, il suffit de remarquer que la norme de a ainsi que celle de l'adjoint est celle de la forme bilinéaire ou sesquilinéaire qui à x et y associe (a(x) | y) = (x | a*(y)).

  • Si l'opérateur a est borné alors la norme de la composée de a et de son adjoint est égal au carré de celle de a :
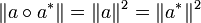
\|a\circ a^*\|=\|a\|^2=\|a^*\|^2

Orthogonalité

Les propriétés d'orthogonalités associées aux formes bilinéaires sont présentes dans ce contexte :

  • Le noyau de a est égal à l'orthogonal de l'image de a* et le noyau de a* est égal à l'orthogonal de l'image de a.
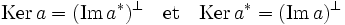
\text{Ker}\,a = (\text{Im}\,a^*)^{\bot}\quad \text{et}\quad \text{Ker}\,a^* = (\text{Im}\,a)^{\bot}

La démonstration est immédiate, elle provient de la chaîne d'équivalences suivante :

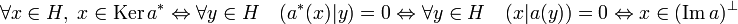
\forall x \in H,\;x \in \text{Ker}\,a^{*} \Leftrightarrow \forall y \in H\quad (a^*(x)|y)=0 \Leftrightarrow \forall y \in H\quad (x|a(y))=0\Leftrightarrow x \in (\text{Im}\, a)^{\bot}

Un corollaire immédiat est qu'en dimension finie a et a* ont même rang car l'orthogonal d'un espace vectoriel fermé est un supplémentaire. En cas de dimension infinie, si a est injective, alors a* possède une image dense dans H, ce qui ne signifie pas que a* est surjective.

Une démonstration analogue permet d'établir le résultat suivant :

  • L'orthogonal du noyau de a est égal à l'adhérence de l'image de l'adjoint de a. De même, l'adhérence de l'image de a est l'orthogonal du noyau de l'adjoint.
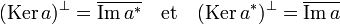
(\text{Ker}\,a)^{\bot} = \overline{\text{Im}\,a^*}\quad \text{et}\quad (\text{Ker}\,a^*)^{\bot} = \overline{\text{Im}\,a}

L'adhérence d'un ensemble E est le plus petit fermé qui le contient, il est ici noté \scriptstyle {\overline E}. En dimension finie, tout sous-espace est fermé et l'orthogonal du noyau de a est égal à l'image de l'adjoint de a.

  • Soit E un sous-espace stable par a, l'orthogonal de E est stable par a*.

La démonstration est de même nature que la précédente. Soit y un élément de l'orthogonal de E, son image par a* est orthogonal à E.

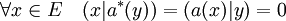
\forall x\in E\quad (x|a^*(y))=(a(x)|y)=0

Application adjointe

Il est possible de considérer l'application * de L(H) dans lui-même, qui à l'opérateur a associe l'adjoint a*. Cette fonction est dénommée l'application adjointe.

L'espace de départ L(H) dispose non seulement d'une structure d'espace vectoriel mais aussi d'algèbre associative avec pour multiplication interne la loi de composition. Il est possible de considérer une autre multiplication interne \scriptstyle \star définie par :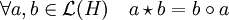

\forall a,b \in \mathcal L(H) \quad a\star b = b\circ a

L'espace L(H)op désigne l'algèbre L(H) munie de la multiplication \scriptstyle \star:

  • L'application adjointe est un isomorphisme isométrique antilinéaire d'algèbre de L(H) dans L(H)op.

Dire que l'application adjointe est un isomorphisme d'algèbre revient à dire, qu'en plus de la conservation de la linéarité, la propriété suivante est vérifiée :

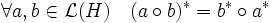
\forall a,b \in \mathcal L(H) \quad (a\circ b)^* = b^*\circ a^*

Cette propriété signifie que :

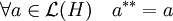
\forall a \in \mathcal L(H) \quad a^{**} = a

En dimension finie, une involution est une symétrie, c'est-à-dire un endomorphisme diagonalisable de valeurs propres 1 et -1, d'espaces propres associés deux espaces supplémentaires. Cette propriété est générale sur tous les Hilbert.

  • L'espace L(H) admet deux sous-espaces supplémentaires espaces propres pour l'application adjointe de valeurs propres 1 et -1. Un vecteur propre de valeur propre associée 1 (resp. -1) est appelé autoadjoint (resp. antisymétrique).
  • En dimension finie l'espace propre de valeur propre associée 1 (resp. -1) est de dimension n(n + 1)/2 (resp. n(n - 1)/2) si n désigne la dimension de H.

En dimension finie et si le corps K est celui des complexes, les endomorphismes autoadjoints et antisymétriques sont diagonalisables, c'est-à-dire qu'il existe une base de E de vecteurs propres. Cette propriété est vraie pour tous les endomorphismes normaux, c'est-à-dire ceux qui commutent avec leur adjoint. Les automorphismes orthogonaux sont normaux et donc diagonalisable.

Si le corps K est celui des réels, les endomorphismes autoadjoints sont toujours diagonalisables.

Démonstrations
  • L'application adjointe est un isomorphisme isométrique antilinéaire d'algèbre de L(H) dans L(H)op :

L'antilinéarité découle directement du caractère sesquilinéaire du produit scalaire :

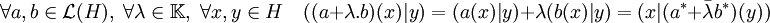
\forall a,b \in \mathcal L(H),\;\forall \lambda \in \mathbb K,\; \forall x,y\in H\quad ((a+\lambda.b)(x)|y)=(a(x)|y) + \lambda(b(x)|y)=(x|(a^* +\bar \lambda b^*)(y))

La conservation de la multiplication interne se démontre de manière analogue :

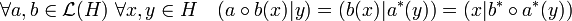
\forall a,b \in \mathcal L(H)\; \forall x,y\in H\quad(a\circ b(x)|y)=(b(x)|a^*(y))=(x|b^*\circ a^*(y))
  • L'application adjointe est involutive :

Cette propriété est la conséquence du caractère hermitien du produit scalaire :

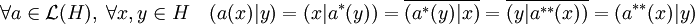
\forall a \in \mathcal L(H),\; \forall x,y\in H\quad (a(x)|y)=(x|a^*(y))= \overline {(a^*(y)|x)} = \overline {(y|a^{**} (x))}=(a^{**}(x)|y)
  • L'espace L(H) admet deux sous-espaces supplémentaires espaces propres pour l'application adjointe de valeurs propres 1 et -1 :

Considérons l'application pde L(H) dans lui-même qui à un opérateur a associe 1/2(a + a*). Cette application est une projection sur l'espace des opérateurs autoadjoints parallèlement à l'espace des antisymétriques. Les propriétés des projecteurs permettent de conclure.

  • En dimension finie l'espace propre de valeur propre associée 1 (resp. -1) est de dimension n(n + 1)/2 (resp. n(n - 1)/2) si n désigne la dimension de H :

Considérons l'application de L(H) dans l'ensemble L2(H) l'espace des formes sesquilinéaires. Cette application est un isomorphisme qui envoie l'espace des autoadjoints (resp. antisymétriques) sur les formes symétriques (resp. alternées). Comme les formes symétriques (resp. alternées) forment un espace vectoriel de dimension n(n + 1)/2 (resp. n(n - 1)/2) la proposition est démontrée.

Remarque : Plus de détails sont donnés dans l'article Forme bilinéaire.

 

Spectre

Le spectre d'un opérateur a correspond à l'ensemble des scalaires λ tel que l'application a - λ.Id n'est pas bijective. Ici, Id désigne l'application identité. En dimension finie le spectre est l'ensemble des valeurs propres. Dans le cas général le spectre est plus large de l'ensemble des valeurs propres. En effet, soit (en) une base de Hilbert de H, dans cet exemple l'espace est supposé séparable et il admet donc une base dénombrable (cf l'article Espace préhilbertien). L'application qui à en associe 1/n.en est non surjective. En effet la série de terme général 1/n.en n'admet pas d'antécédent. La valeur zéro est donc élément du spectre. Pourtant l'application est injective, donc zéro n'est pas valeur propre.

  • Le spectre de l'opérateur a* est le conjugué de celui de a.

Les propriétés du spectre se généralisent si H est de dimension finie :

  • Si H est de dimension finie, le déterminant (resp. le polynôme caractéristique) de l'adjoint de a est égal à son conjugué.

Il est possible de choisir une approche par le polynôme minimal :

  • Si H et de dimension finie le polynôme minimal de a est le conjugué de celui de a*.

En conséquence, si λ est valeur propre de multiplicité m de l'opérateur a (la multiplicité est le plus petit entier tel que le noyau de (a -λId)m est égal au noyau de (a -λId)m+1), alors le conjugué de λ est valeur propre de multiplicité m pour l'opérateur a* et :

  • En dimension finie, un sous-espace caractéristique de a de valeur propre λ est un sous-espace caractéristique de l'adjoint de valeur propre le conjugué.
Démonstrations
  • Le spectre de l'opérateur a* est le conjugué de celui de a :

Les propriétés d'orthogonalités montrent que si a n'est pas injectif, alors l'adjoint n'est pas surjectif. De même si a n'est pas surjectif, alors l'adjoint n'est pas injectif. Si l'opérateur a - λId n'est pas bijectif, alors son adjoint ne l'est pas non plus, ce qui montre que le conjugué de λ est une valeur spectrale de a*.

  • Si H est de dimension finie, le déterminant (resp. le polynôme caractéristique) de l'adjoint de a est égal à son conjugué :

L'article Déterminant (mathématiques) démontre qu'une matrice carrée possède le même déterminant que sa transposée. De plus, le déterminant d'une matrice conjuguée est le conjugué du déterminant. Le fait que le déterminant d'un endomorphisme est égal à celui de sa matrice montre que le déterminant de l'adjoint de a est le conjugué de celui de a. Les mêmes propriétés appliquées à l'endomorphisme a - λId montre l'égalité des polynômes caractéristiques.

  • Si H et de dimension finie le polynôme minimal de a est le conjugué de celui de a* :

Soit P[X] le polynôme minimal de a. L'endomorphisme P[a] est nul et son conjugué l'est aussi, ce qui montre que le polynôme conjugué de P[X] annule l'adjoint, son conjugué est donc un multiple du polynôme de a*. On montre de même que le polynôme conjugué du polynôme minimal de l'adjoint annule a. Les deux polynômes sont multiples l'un de l'autre, ils sont tous deux unitaires, ce qui permet de conclure à l'égalité.

  • En dimension finie, un sous-espace caractéristique de a de valeur propre λ est un sous-espace caractéristique de l'adjoint de valeur propre le conjugué :

Un sous-espace caractéristique E est stable pour a, il est aussi stable sur son adjoint. Sur E, il existe m tel que l'endomorphisme (a -λId)m est nul. Le conjugué de cet endomorphisme est donc aussi nul sur E, ce qui termine la démonstration.

 

Espace de Banach

De nombreuses propriétés, valables pour les Hilbert peuvent être généralisées. L'analyse de l'adjoint d'un opérateur dans le cadre plus général des Banach possède des analogies certaines avec le cas précédent. Les techniques utilisées sont néanmoins un peu différentes. Dans ce paragraphe E et F désignent des Banach et a un opérateur non borné de E dans F.

Le terme opérateur non borné désigne une application linéaire sans précision sur le caractère continu de l'opérateur. Le mathématicien Haïm Brezis précise : Il peut donc arriver qu'un opérateur non borné soit borné. La terminologie n'est pas très heureuse, mais elle est communément répandue et elle n'engendre pas de confusion ![4]

Existence et unicité

Comme précédemment, tout opérateur a admet un unique adjoint. Plus précisément :

  • Pour tout opérateur non borné a de D(a) dans F il existe un unique adjoint, et l'adjoint est linéaire.

La question se pose alors de savoir si D(a*) est dense dans le dual de F.

  • Si a est un opérateur fermé, alors pour la topologie faible du dual de F, D(a*) est dense dans le dual de F. Si de plus F est reflexif alors D(a*) est dense pour la topologie usuelle.
Démonstration
  • Pour tout opérateur non borné a de D(a) dans F il existe un unique adjoint, et l'adjoint est linéaire.

Remarquons dans un premier temps que D(a*) est un espace vectoriel. Soit y1* (resp. y2*) un vecteur de D(a*), λ un élément de K et c1 (resp. c2) une constante vérifiant la propriété suivante :

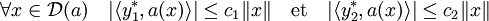
\forall x \in \mathcal D(a) \quad |\langle y_1^*,a(x)\rangle|\le c_1\|x\| \quad \text{et}\quad |\langle y_2^*,a(x)\rangle|\le c_2\|x\|

La majoration suivante montre que y1* + λy2* est bien élément de D(a*).

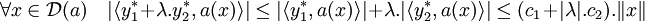
\forall x\in \mathcal D(a) \quad |\langle y_1^*+\lambda .y_2^*,a(x)\rangle|\le |\langle y_1^*,a(x)\rangle| + \lambda.|\langle y_2^*,a(x)\rangle|\le (c_1 +|\lambda |.c_2).\|x\|

Soit y* un élément de D(a*). Par défaut, a*(y*) est une forme linéaire continue sur D(a). L'ensemble d'arrivé K est complet la forme est continue donc uniformément continue et se prolonge par continuité de manière unique (cf l'article Continuité uniforme). Ainsi, l'application a*(y*) est bien un élément de E*.

La linéarité de a* provient directement de la bilinéarité de <.,.>.

 

Continuité de l'adjoint

Le théorème du graphe fermé indique qu'un opérateur a est continu si et seulement si son graphe est fermé. Le graphe de a est le sous-espace vectoriel de ExF formé des points (x, a(x)) quand x parcourt D(a). Un opérateur ayant un graphe fermé est dit fermé, ce qui revient à dire borné ou continue. Pour une raison de style, il est plus fréquent de parler d'un opérateur non borné fermé que d'un opérateur non borné borné, même si les significations sont identiques.

  • Un opérateur non borné a à domaine dense possède un adjoint fermé.
Démonstration

La démonstration est relativement simple. Soient (vn*) une suite de D(a*) convergente vers v* dans le dual de F et tel que la suite (a*(vn*)) converge aussi, mais cette fois çi vers u* dans le dual de E. L'objectif est de montrer que (v*, u*) est un élément du graphe de l'adjoint de a. L'égalité suivante est vérifiée :

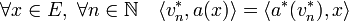
\forall x \in E,\;\forall n \in \mathbb N \quad \langle v_n^*, a(x)\rangle =\langle a^*(v_n^*), x\rangle

Un passage à la limite montre que :

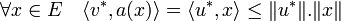
\forall x \in E \quad \langle v^*, a(x)\rangle =\langle u^*, x\rangle \le \|u^*\|.\|x\|

La dernière majoration montre que v* est un élément de D(a*) et la dernière égalité montre que u* est l'image de v* par a*. En conséquence le point (v*, u*) est un élément du graphe de a*, ce qui démontre la proposition.

 

Orthogonalité

Si a est fermé et possède un domaine dense, alors les propriétés d'orthogonalités correspondant à la situation hilbertienne restent vraies :

  • Le noyau de a est égal à l'orthogonal de l'image de a* et le noyau de a* est égal à l'orthogonal de l'image de a.
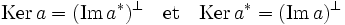
\text{Ker}\,a = (\text{Im}\,a^*)^{\bot}\quad \text{et}\quad \text{Ker}\,a^* = (\text{Im}\,a)^{\bot}

La situation diffère légèrement pour l'orthogonal des noyaux.

  • L'orthogonal du noyau de a contient l'adhérence de l'image de l'adjoint de a et l'orthogonal du noyau de l'adjoint de a est l'adhérence de l'image de a.
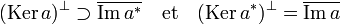
(\text{Ker}\,a)^{\bot} \supset \overline{\text{Im}\,a^*}\quad \text{et}\quad (\text{Ker}\,a^*)^{\bot} = \overline{\text{Im}\,a}

Si l'espace E est réflexif, alors l'orthogonal du noyau de a est égal à l'adhérence de l'image de a*, dans le cas contraire, l'égalité n'est pas assurée.

Avec les hypothèse de fermeture et de densité du domaine de a :

  • Les quatre propriétés suivantes sont équivalentes :
(1) L'image de a est fermée.
(2) L'image de l'adjoint de a est fermée.
(3) L'image de a est l'orthogonal du noyau de l'adjoint.
(4) L'image de l'adjoint est l'orthogonal du noyau de a.
Démonstrations
  • Le noyau de a est égal à l'orthogonal de l'image de a* et le noyau de a* est égal à l'orthogonal de l'image de a :

On remarque que, comme a est continue, le domaine de a* est le dual de F entier, donc :

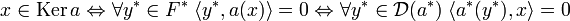
x\in \text{Ker}\,a \Leftrightarrow \forall y^* \in F^* \; \langle y^* ,a(x)\rangle = 0 \Leftrightarrow \forall y^* \in \mathcal D(a^*) \; \langle a^*(y^*),x\rangle = 0

Ce qui démontre la première égalité.

On remarque que, comme D(a) est dense dans E, un vecteur du dual de E est nul si et seulement s'il est orthogonal à D(a), donc :

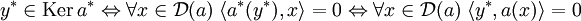
y^*\in \text{Ker}\,a^* \Leftrightarrow \forall x \in \mathcal D(a) \; \langle a^*(y^*) ,x\rangle = 0 \Leftrightarrow \forall x \in \mathcal D(a) \; \langle y^*,a(x)\rangle = 0

Ce qui démontre la deuxième égalité.

  • L'orthogonal du noyau de a contient l'adhérence de l'image de l'adjoint de a et l'orthogonal du noyau de l'adjoint de a est l'adhérence de l'image de a :

L'étude des formes bilinéaires continues montre que l'orthogonal d'un d'orthogonal d'un espace vectoriel contient l'adhérence de l'espace initiale. L'orthogonal de l'orthogonal de l'image de d'adjoint de a contient donc l'adhérence de l'image de l'adjoint de a. La proposition précédente permet de conclure pour l'inclusion suivante :

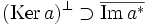
(\text{Ker}\,a)^{\bot} \supset \overline{\text{Im}\,a^*}
 

Surjectivité

Conséquence de la continuité de a

Références

Notes

  1. ↑ Cette définition de l'adjoint se trouve par exemple dans la référence : S. Lang Analyse Réelle InterEditions, Paris 1977 (ISBN 2729600595) p 157
  2. ↑ J. Dixmier, Les C*-algèbres et leurs représentations, Gauthier-Villars, 1969 (ISBN 0720407621)
  3. ↑ La définition utilisée ici se trouve dans de nombreuses références. On peut citer Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions] p 27
  4. ↑ Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions] p 27

Liens externes

Références

  • W. Rudin Analyse réelle et complexe : Cours et exercices Dunod 3ème Ed 1998 (ISBN 2100040049)
  • Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
  • Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
  • J. Lindenstrauss L. Tzafriri Classical Banach Spaces Vol I Springer 1996 (ISBN 3540606289)
  • G. Pedersen C*-algebras and their automorphism groups Academic Press, London and New-York, 1979
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Op%C3%A9rateur adjoint ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Adjoint d'un endomorphisme de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Adjoint D'un Endomorphisme — Opérateur adjoint En mathématiques l adjoint d un opérateur, quand il existe, est un nouvel opérateur défini sur un espace vectoriel sur le corps des nombres réels ou complexes et munis d un produit scalaire. Un tel espace est qualifié de… …   Wikipédia en Français

  • Endomorphisme auto-adjoint — Endomorphisme autoadjoint En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d application linéaire. Cette propriété s applique à une application linéaire d un espace vectoriel dans lui… …   Wikipédia en Français

  • Endomorphisme Autoadjoint — En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d application linéaire. Cette propriété s applique à une application linéaire d un espace vectoriel dans lui même ; pour cette… …   Wikipédia en Français

  • Endomorphisme Normal — Définition Soit un espace préhilbertien, réel ou complexe. Soit un endomorphisme de admettant un adjoint . On dit que est normal si …   Wikipédia en Français

  • Endomorphisme antiautoadjoint — ● Endomorphisme antiautoadjoint endomorphisme admettant un endomorphisme adjoint et égal à l opposé de celui ci …   Encyclopédie Universelle

  • Endomorphisme antisymétrique — ● Endomorphisme antisymétrique endomorphisme admettant un endomorphisme adjoint et égal à l opposé de celui ci …   Encyclopédie Universelle

  • Endomorphisme autoadjoint — ● Endomorphisme autoadjoint endomorphisme admettant un adjoint et égal à celui ci …   Encyclopédie Universelle

  • Auto-adjoint — Endomorphisme autoadjoint En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d application linéaire. Cette propriété s applique à une application linéaire d un espace vectoriel dans lui… …   Wikipédia en Français

  • Endomorphisme autoadjoint — En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint ou opérateur hermitien est un endomorphisme d espace de Hilbert qui est son propre adjoint (sur un espace de Hilbert réel on dit aussi endomorphisme… …   Wikipédia en Français

  • Endomorphisme normal — Un endomorphisme normal est un opérateur d un espace de Hilbert qui commute avec son adjoint. Sommaire 1 Définition 2 Exemples 3 Propriétés 4 Article connexe …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”