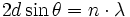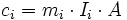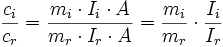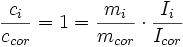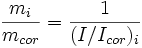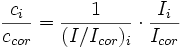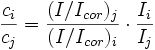Diffraction X

La diffractométrie de rayons X (DRX, on utilise aussi souvent l'abréviation anglaise XRD pour X-ray diffraction) est une technique d'analyse basée sur la diffraction des rayons X sur la matière. La diffraction n'ayant lieu que sur la matière cristalline, on parle aussi de radiocristallographie. Pour les matériaux non-cristallins, on parle de diffusion.

L'appareil de mesure s'appelle un diffractomètre. Les données collectées forment le diagramme de diffraction ou diffractogramme.

Sommaire 1 Présentation générale 2 Interaction rayons X-matière 3 Applications de la DRX 3.1 Identification de phases cristallines 3.1.1 Principes de l'identification des phases 3.1.2 Problèmes rencontrés 3.1.3 Algorithmes manuels d'identification des phases 3.1.3.1 Méthode d'Hanawalt 3.1.3.2 Méthode Fink 3.1.4 Algorithmes informatiques d'identification des phases 3.2 Analyse quantitative 3.2.1 Méthode des surfaces de pic 3.2.2 Rapport d'intensité de référence 3.2.3 Méthode de Rietveld 3.3 Mesure de contraintes 3.4 Mesure de la texture 3.5 Détermination de structures cristallographiques 4 Annexes 4.1 Bibliographie 4.2 Articles connexes 4.3 Liens externes 4.4 Références

Présentation générale

Qu'est-ce que c'est ?

La diffractométrie de rayons X est une méthode d'analyse physico-chimique. Elle ne marche que sur la matière cristallisée (minéraux, métaux, céramiques, produits organiques cristallisés), mais pas sur la matière amorphe (liquides, polymères, verres) ; toutefois, la matière amorphe diffuse les rayons X, et elle peut être partiellement cristallisée, la technique peut donc se révéler utile dans ces cas-là. Par contre, elle permet de reconnaître des produits ayant la même composition chimique brute, mais une forme de cristallisation différente, par exemple de distinguer les différentes silices (qui ont toutes la même formule brute SiO₂ : quartz, cristobalite…), les différents aciers (acier ferritique, austénite…) ou les différentes alumines (qui ont toutes la même formule brute Al₂O₃ : corindon/alumine α, γ, δ, θ…).

Comment ça marche ?

On prépare l'échantillon sous la forme d'une poudre aplanie dans une coupelle, ou bien sous la forme d'une plaquette solide plate. On envoie des rayons X sur cet échantillon, et un détecteur fait le tour de l'échantillon pour mesurer l'intensité des rayons X selon la direction. Pour des raisons pratiques, on fait tourner l'échantillon en même temps, ou éventuellement on fait tourner le tube produisant les rayons X.

Qui utilise cette technique ?

La technique est utilisée pour caractériser la matière. Cela concerne :

• la recherche : lorsque l'on crée un nouveau matériau (souvent des céramiques), que l'on veut connaître le résultat d'une réaction chimique ou physique (par exemple en métallurgie, pour reconnaître les produits de corrosion ou savoir quel type d'acier on a fabriqué), en géologie (géochimie) pour reconnaître la roche prélevée à un endroit ;
• pour le suivi de production dans une usine (contrôle de la qualité du produit) : dans les cimenteries, les fabriques de céramiques…
• l'industrie pharmaceutique :
  • en recherche : les nouvelles molécules sont cristallisées, et les cristaux sont étudiés par diffractométrie de rayons X ;
  • en production : cela sert notamment à vérifier que l'on n'a pas fabriqué une autre molécule de même formule, mais de forme différente (on parle de polymorphisme)

Interaction rayons X-matière

Les rayons X, comme toutes les ondes électromagnétiques, provoquent un déplacement du nuage électronique par rapport au noyau dans les atomes ; ces oscillations induites provoquent une réémission d'ondes électromagnétiques de même fréquence ; ce phénomène est appelé diffusion Rayleigh.

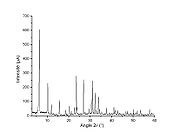
La longueur d'onde des rayons X étant de l'ordre de grandeur des distances interatomiques (quelques angström), les interférences des rayons diffusés vont être alternativement constructives ou destructives. Selon la direction de l'espace, on va donc avoir un flux important de photons X, ou au contraire très faible ; ces variations selon les directions forment le phénomène de diffraction X.

Ce phénomène a été découvert par Max von Laue (Prix Nobel en 1914), et longuement étudié par sir William Henry Bragg et son fils sir William Lawrence Bragg (prix Nobel commun en 1915),

Les directions dans lesquelles les interférences sont constructives, appelées « pics de diffraction », peuvent être déterminées très simplement par la formule suivante, dite loi de Bragg :

avec

• d = distance interréticulaire, c'est-à-dire distance entre deux plans cristallographiques ;
• θ = demi-angle de déviation (moitié de l'angle entre le faisceau incident et la direction du détecteur) ;
• n = ordre de réflexion (nombre entier) ;
• λ = longueur d'onde des rayons X.

Comme les plans cristallographiques peuvent être repérés par les indices de Miller {hkl}, on peut indexer les pics de diffraction selon ces indices.

Applications de la DRX

Identification de phases cristallines

Principes de l'identification des phases

L'idée d'utiliser la diffraction des rayons X pour identifier une phase fût développée au début du XX^e siècle de manière indépendante par Albert Hull^[1],[2] en 1919 d'une part, et par Peter Debye et Paul Scherrer d'autre part^[3]. En raison de la guerre, la publication et la diffusion des journaux scientifiques était difficile ; chronologiquement, c'est Hull qui publia le premier ses travaux , mais la méthode porte le nom de Debye et Scherrer.

Une poudre formée d'une phase cristalline donnée va toujours donner lieu à des pics de diffraction dans les mêmes directions, avec des hauteurs relatives à peu près constantes. Ce diagramme de diffraction forme ainsi une véritable signature de la phase cristalline. Il est donc possible de déterminer la nature de chaque phase cristalline au sein d'un mélange (mélange de poudre ou échantillon massif polyphasique), à condition d'avoir auparavant déterminé la signature de chaque phase.

La détermination de cette signature peut se faire soit de manière expérimentale (mesure d'un produit pur dans des conditions idéales), soit par simulation numérique à partir de la structure cristallographique connue — structure ayant elle-même pu être déterminée par diffraction X (cf. ci-dessous). Cette signature est consignée dans une fiche sous la forme d'une liste de pics ; la position en 2θ est convertie en distance interréticulaire d par la loi de Bragg, afin d'avoir une valeur indépendante de la longueur d'onde des rayons X (et donc du type de source de rayons X utilisée). L'intensité I de chaque pic est exprimée en pourcent %, parfois en pourmille ‰, 100 % (ou 1 000 ‰) étant la hauteur du pic le plus intense. Cette liste de pics est souvent désignée par le terme « liste de d—I » . On constitue ainsi des bases de données, et le diagramme mesuré sur le produit inconnu est comparé de manière informatique à toutes les fiches de la base de données. La base de données la plus complète à l'heure actuelle (2004) est la Powder diffraction file (PDF) de l'ICDD (ex-JCPDS : Joint committee on powder diffraction standards, ex- comité E4 de l'ASTM), avec plus de 150 000 fiches (dont cependant de nombreuses redondances).

L'intérêt de cette méthode est qu'elle permet de distinguer les différentes formes de cristallisation d'un même composé (par exemple pour la silice, distinguer le quartz de la cristobalite). Cependant, elle ne peut généralement pas permettre d'identifier des composés amorphes. Cette technique est donc complémentaire de l'analyse élémentaire.

La procédure d'identification des phases se fait en deux étapes : une étape de recherche dans une base (search), puis une confrontation des fiches probables avec ce qui est possible chimiquement (match) ; on parle donc fréquemment de search/match pour désigner cette procédure.

Au final, c'est l'utilisateur qui détermine si un produit est présent ou pas : en raison des possibilités de confusion (plusieurs produits très différents pouvant avoir des signatures très proches), un algorithme automatisé ne peut pas prendre seul la décision. C'est en dernier ressort la compétence de l'utilisateur, son habileté et sa connaissance de l'échantillon qui interviennent.

Dans certains domaines, on veut simplement savoir si l'on n'a que la ou les phases prévues et pas d'autre (— notamment, problème des polymorphes) dans le suivi de la production pharmaceutique. Dans ce contexte, il suffit d'établir une liste de pics sur le diffractogramme du produit inconnu, que l'on compare à une liste de pics établie sur le diffractogramme d'un produit étalon (c'est-à-dire dont la composition chimique est maîtrisée).

Problèmes rencontrés

Dans le cas d'un produit réellement inconnu et dont on cherche à identifier toutes les phases, on est confronté principalement à trois problèmes :

• l'écart de la signature d'un produit par rapport à sa signature théorique ou idéale :
  • la position en 2θ des pics d'une phase peuvent être décalés :
    • problème d'alignement du diffractomètre,
    • problème de hauteur de la surface de l'échantillon ;
    • problème de variation des paramètres de la maille cristalline, en raison des contraintes ou de la solution solide — produit non pur,
  • les hauteurs relatives des pics ne sont que rarement respectées :
    • orientation préférentielle,
    • nombre de cristallites insuffisants pour avoir une bonne statistique,
    • superposition de pics ;
• le mélange des pics est parfois complexe, avec des superpositions ;
• il faut comparer le diffractogramme avec plusieurs centaines de milliers de fiches de référence.

Algorithmes manuels d'identification des phases

Méthode d'Hanawalt

Le premier algorithme fut inventé par Hanawalt en 1936^[4],[5],[6]. À l'époque, les fiches de référence étaient sous forme papier. Hanawalt regroupa les fiches dont le pic principal (dit « pic à 100 % ») étaient au même endroit (ou plus précisément dans une même zone 2θ restreinte), les catégories ainsi crées étant classées par ordre croissant de position 2θ ; puis, dans une catégorie de fiches, il regroupa les fiches dont le second pic le plus intense étaient au même endroit, classant de même les sous-catégories, et dans une sous-catégorie, il classa les fiches par ordre de position du troisième pics le plus intense. Pour dépouiller un diffractogramme, il procédait donc ainsi :

• on déterminait les trois pics les plus intenses, et on recherchait dans la liste d'Hanawalt la ou les fiches pouvant correspondre ;
• le premier produit étant identifié, on éliminait les trois pics considérés et on recommençait.

Cette méthode porte aussi le nom de « méthode ASTM »^[7].

Cependant, il fallait aussi prendre en compte les possibles superpositions de pics, donc la possibilité qu'un pic appartenant à une phase déjà identifiée appartienne également à une autre phase. De fait, l'identification devenait extrêmement complexe au-delà d'un mélange de trois phases, et était peu performante pour détecter les phases présentes en faible quantité, c'est-à-dire générant des pics de faible hauteur.

Méthode Fink

La méthode Fink^[8] fut développée par W. Bigelow et J. V. Smith de l'ASTM au début des années 1960, qui lui donnèrent le nom de William Fink, un référent du JCPDS. L'idée est de considérer les quatre pics les plus intenses d'une fiche, d'appliquer toutes les permutations possibles, puis de classer toutes ces solutions par ordre de d croissant. Lors d'une recherche, l'opérateur prend la première valeur de d rencontrée sur le diffractogramme, puis cherche dans l'index les fiches auxquelles ce pic pourrait appartenir. Les autres pics de chaque fiche sont ensuite confrontés au diffractogramme.

Algorithmes informatiques d'identification des phases

L'informatique a permis d'automatiser les procédures manuelles, notamment avec des algorithmes de recherche automatique de pics et des comparaisons avec les fiches sous formes électroniques. Elle a aussi permis d'améliorer l'algorithme, en multipliant les comparaisons possibles au lieu de se contenter des trois pics les plus intenses. Elle a aussi permis de croiser les informations sur les pics avec des informations sur la composition chimique (recherche dite « booléenne » car elle utilise des opérations logiques du type « et », « non » et « ou »).

Les premiers programmes sont apparus au milieu des années 1960, avec des limitations inhérentes à la qualité des diffractogrammes et aux capacités de calcul des ordinateurs : les programmes devaient considérer des possibilités d'erreur importantes sur les valeurs de d et de I.

M. C. Nichols^[9],[10] adapte ainsi l'algorithme d'Hanawalt en 1966. G. G. Johnson Jr. et V. Vand adoptent quant à eux une approche résolument nouvelle en 1965^[9],[11] : ils comparent de manière systématique toutes les fiches de la base de donnée avec la liste de d–I extraite du diffractogramme, et donnent une note à la fiche (FOM, figure of merit). Les fiches de la base de données sont donc classées par ordre de note de correspondance, puis les « meileurs élèves » sont affichés (typiquement, on affiche les 50 premiers), classés selon le nombre de pics communs à la fiche et à la liste de d–I extraite du diffractogramme, puis selon la note.

En 1982, le fabriquant Philips développe un algorithme propriétaire (non publié) basé sur la méthode des moindres carrés^[12] : la note pour chaque fiche est calculée en fonction de l'écart entre les pics de la fiche de référence et la liste de d–I extraite du diffractogramme.

L'amélioration récente la plus importante a eu lieu en 1986^{[13],[14],[15]}, avec le programme commercial Eva (suite logicielle DIFFRAC-AT, puis DIFFRAC^plus) de la société Socabim, une PME française travaillant essentiellement pour le fabriquant Siemens. Cet algorithme propriétaire (non publié) reprend la logique de Johnson et Vand ; cependant, il ne se contente pas d'extraire une liste de pics du diffractogramme, mais compare chaque fiche avec le diffractogramme lui-même pour donner une note à la fiche (mieux la fiche correspond au diffractogramme, plus la note est basse). Les fiches de la base de données sont donc classées par ordre de correspondance, puis les « meilleurs élèves » sont affichés (typiquement, on affiche les 50 premiers) ; l'utilisateur superpose ensuite les fiches (représentées sous la forme de bâtons) au diffractogramme pour déterminer les fiches qu'il retient. Ainsi, l'algorithme utilise la totalité des points mesurés, et notamment la ligne de fond, au lieu de se contenter d'une liste restreinte de sommet de pics ; il prend en compte la superposition des pics (si le bâton d'une fiche se trouve dans une zone où le signal est au-dessus de la ligne de fond, peu importe qu'il soit seul ou qu'il y ait d'autres bâtons) et permet de détecter les phases minoritaires. D'autres sociétés ont par la suite développé des algorithmes similaires.

Analyse quantitative

Méthode des surfaces de pic

La théorie indique que dans un mélange, la surface nette des pics d'une phase (dite aussi « intensité intégrale ») est proportionnelle à la concentration de la phase moyennant un terme d'absorption : les rayons X sont absorbés par la matière selon une loi de Beer-Lambert, donc 1 % d'un matériau donné ne donne pas le même signal selon les 99 % restant.

On peut donc écrire une loi de la forme :

où

• c_i est la concentration de la phase i ;
• I_i est l'intensité intégrale d'un pic donné de i ;
• m_i est un coefficient d'étalonnage, une constante de du couple appareil/phase ;
• A est le terme d'absorption, qui est le même pour toutes les phases (puisque l'on travaille en rayonnement monochromatique).

Le coefficient d'étalonnage évolue avec l'âge de l'appareil, et notamment le vieillissement du tube à rayons X.

On peut s'abstraire de l'absorption de deux manières (méthodes de Chung) :

• en introduisant un étalon interne : si l'échantillon est sous forme de poudre, on peut mélanger une quantité donnée et connue d'une phase de stable r, et l'on travaille alors en rapport d'intensité et de concentration :

• en utilisant une équation supplémentaire : si toutes les phases soient mesurables et mesurées, la somme des concentrations est égale à 100 %, on a alors autant d'équations que d'inconnues.

Ces deux méthodes permettent également de s'abstraire du vieillissement du tube.

Si les échantillons sont quasiment identiques, on peut considérer que le terme d'absorption est toujours le même et se contenter d'intégrer celui-ci dans le coefficient d'étalonnage. Cependant, cette méthode devient erronée si l'on sort d'une gamme de concentrations restreinte, et il faut refaire l'étalonnage régulièrement pour prendre en compte le vieillissement du tube, ou bien déterminer la variation d'intensité pour la corriger, méthode dite de « correction de dérive » (drift correction).

Rapport d'intensité de référence

Si l'on choisit une méthode de préparation de référence avec un étalon interne donné, il est possible d'établir un coefficient d'étalonnage par défaut ; c'est la méthode dite RIR, pour « rapport d'intensité de référence » (reference intensity ratio).

La méthode qui fait référence est la suivante :

• on prépare l'échantillon sous forme de poudre ;
• on le mélange avec 50 % de corindon (alumine α-Al₂O₃) et on le mesure ;
• on fait le rapport entre le pic le plus grand de la phase et le pic le plus grand de corindon.

Ce rapport d'intensité est appelé I/I_cor, et constitue le coefficient d'étalonnage de référence.

Si maintenant on considère les équations ci-dessus, on a, comme c_i = c_cor :

soit

Dans le cas général c_i ≠ c_cor, on a donc :

En faisant le rapport pour deux phases i et j, on obtient :

On voit alors que les concentration et intensité du corindon disparaissent des formules. On peut donc mesurer l'échantillon inconnu sans ajouter de corindon et utiliser tout de même les coefficients d'étalonnage établis avec le corindon.

Cette méthode est dite « semi-quantitative » car il n'est pas possible de définir l'erreur commise sur la mesure. En effet, comme les échantillons de référence n'ont pas la même nature que l'échantillon inconnu et n'ont pas subit la même préparation, il n'est pas possible d'utiliser l'écart type obtenu sur l'étalonnage pour avoir une estimation de l'erreur. Par ailleurs, l'écart type sur l'étalonnage n'est en général pas fourni.

Méthode de Rietveld

On peut également faire de la quantification par la méthode de Rietveld : on part de concentrations arbitraires, et on simule le diffractogramme que l'on obtiendrait, en utilisant la théorie de la diffraction. Puis, on ajuste les concentrations afin de rapprocher le diffractogramme simulé du diffractogramme mesuré (méthode des moindres carrés).

La méthode de Rietveld est une méthode sans étalon, mais elle nécessite d'acquérir un diffractogramme sur une grande plage angulaire avec une bonne précision (donc une mesure longue), alors que la méthode de l'intensité intégrale permet de ne mesurer que des plages de quelques degrés autour des pics intéressants. Mais la méthode de Rietveld est la seule exploitable si l'on ne peut pas utiliser de pic isolés (problèmes de superposition de pics).

Pour obtenir informatiquement le spectre théorique voulu, l'expérimentateur peut affiner plusieurs paramètres :

• Les paramètres de maille
• Le taux de cristallinité
• La forme des pics (Gaussien ou Lorentzien) et ajustant le coefficient eta.
• La forme du pied des pics (Coefficients de Caglioti)
• Le bruit de fond (polynôme de degré 5 en général)
• Le décalage d'origine
• Le facteur d'échelle

Mesure de contraintes

Si le cristal est comprimé ou étiré, les distances interréticulaires varient. Ceci entraîne une variation de la position des pics.

En mesurant les déplacement des pics, on peut en déduire la déformation de la maille, et donc, à partir des coefficients élastiques, la contrainte résiduelle dans le matériau.

En faisant varier l'orientation de l'échantillon par rapport au vecteur de diffraction (bissectrice entre faisceau incident et faisceau détecté), on peut mesurer la variation de cette contrainte selon l'orientation de l'échantillon, et donc déterminer le tenseur des contraintes.

Mesure de la texture

Une des hypothèses de la diffraction de poudre avec géométrie de Bragg-Brentano est que toutes les orientations cristallines doivent être respectées. En effet, comme le vecteur de diffraction est toujours perpendiculaire à la surface de l'échantillon, un plan (hkl) ne peut donner un pic que s'il existe des cristallites dont le plan (hkl) est parallèle à la surface.

Si l'échantillon n'est pas isotrope, alors certains plans donneront des pics moins élevés, d'autres plus élevés qu'une poudre isotrope. Par ailleurs, si l'on incline l'échantillon, le nombre de cristallites dont le plan (hkl) diffracte va varier ; ainsi, en mesurant la hauteur de deux pics pour plusieurs orientations de l'échantillon, on peut déterminer l'orientation globale des cristallites, c'est-à-dire la texture.

Détermination de structures cristallographiques

À partir des intensités diffractées et de la relation inverse (réseau réciproque—réseau réel), il est possible, à partir d'une série d'images de diffraction, de déterminer l'arrangement tridimensionnel des atomes d'une structure cristalline. Cette méthode a pris une importance considérables ces dernières années pour la détermination de la structure des protéines biologiques.

On part de figure de diffraction sur monocristal (clichés de Laue). À l'aide d'un logiciel (par exemple Denzo), il est possible de déterminer les axes et centres de symétrie d'un cristal et de proposer le système cristallin le plus probable parmi les sept existants (triclinique, monoclinique, orthorhombique, trigonal, tétragonal=quadratique, hexagonal, cubique). C'est ensuite à l'utilisateur de choisir le groupe d'espace le plus approprié : le système choisi est généralement celui qui a la plus haute symétrie afin d'avoir la meilleure résolution (c'est généralement à la fin de l'analyse, lorsque toutes les positions atomiques sont déterminées que peut être précisé le groupe d'espace). Des paramètres de maille sont alors proposés.

Le facteur de fiabilité R (reliability) permet de calculer le degré de fiabilité de la maille proposée par rapport à la structure cristalline réelle. Quand il atteint une valeur suffisamment faible cela signifie que le modèle de maille est acceptable ; on peut alors passer à l'étape suivante c'est-à-dire l'intégration des intensités diffractées et l'affinement des paramètres de maille.

Les amplitudes diffractées sont caractéristiques de la nature et de la position des atomes, en fait de la densité électronique en tout point de la maille. Plus exactement, espace réel (de la structure cristalline) et réciproque (des directions de diffraction) sont liés par transformation de Fourier. Malheureusement, une partie importante de l'information est perdue lors de la collection des images de diffraction, puisque seule la norme des intensités complexes est mesurable par les détecteurs. Les phases, qui portent une part très importante de l'information structurale, sont perdues et doivent êtres déterminées (expérimentalement et/ou informatiquement). Il est nécessaire d'intégrer un grand nombre de « taches », correspondant à l'intensité des réflexions sur le réseau cristallin.

Pour les petits composés (mailles contenant peu d'atomes), des procédures ab initio ont été mises au point. Par contre, pour des composés de masse molaire (ou poids moléculaire) plus importante, on utilise des méthodes :

• de dérivation aux atomes lourds ;
• anomales ;
• ou bien de remplacement moléculaire, quand la structure (de l'unité asymétrique) est partiellement connue.

Par itérations successives, il est alors possible de déterminer les phases manquantes, et par là même d'affiner la structure cristallographique du composé.

Dans certains cas, on peut utiliser la méthode de Rietveld sur des diffractogrammes de poudre. La préparation est bien moins contraignante — il n'est pas nécessaire d'obtenir un « gros » monocristal —, mais le diffractogramme de poudres contient moins d'informations qu'un cliché de Laue, puisque l'on perd la répartition de l'intensité autour du vecteur de diffraction.

Annexes

Bibliographie

• Méthodes physiques d'étude des minéraux et des matériaux, J.-P. Eberhart, éd. Doin éditeurs, 1976
• Elements of X-ray Diffraction, B. D. Cullity, éd. Addison-Wesley, 1956
• Introduction to X-ray Powder Diffraction, R. Jenkins, R. L. Snyder, éd. Wiley Interscience, 1996
• A computerized powder identification system, G. G. Johnson Jr., V. Vand, Ind. Eng. Chem vol. 59, p19, 1965
• A Fortran II program for the identification of X-ray powder diffraction patterns, M. C. Nichols, UCRL-70078, 1966
• A new minicomputer search/match/identify program for qualitative phase analysis with the powder diffractometer, W. N. Schreiner, C. Surdukowski, R. Jenkins, J. Appl. Crystallogr. vol. 15, pp 513–523, 1982
• Using digitized X-ray powder diffraction scans as input for a new PC-AT Search/match program, P. Caussin, J. Nusinovici, D. W. Beard, Adv. X-Ray Anal. vol. 31, pp 423–430, 1988
• Powder diffraction, J. Ian Ianford, D. Louër, Rep. Prog. Phys. vol. 59, pp 131–234, 1996
• Chemical Analysis by X-Ray Diffraction, J. D. Hannawalt, H. W. Rinn et L. K. Fevel, Ind. Eng. Chem., Anal. Ed. 10, pp 457–512, 1938
• A New Method of Chemical Analysis, A. W. Hull, J. Am. Chem. Soc. 41, pp 1168–1195, 1919
• [pdf] Autobiography, A. W. Hull, Fifty Years of X-Ray Diffraction, IUCr
• [pdf] Personal Reminescences, P. Scherrer, Fifty Years of X-Ray Diffraction, IUCr
• [pdf] Fast residual stress mapping using energydispersive synchrotron X-ray diffraction, Alexander M. Korsunsky, Steve P. Collins, R. Alexander Owen, Mark R. Daymond, Saïda Achtioui et Karen E. James 2002

Articles connexes

• Simulation de profil
• Générateur de rayons X

Liens externes

• (en) Liste de diffusion xrd@jiscmail.ac.uk
• Diffraction des rayons X
• (en) X-ray based methods of analysis, K. Janssens, Université d'Anvers
• Logiciels de traitement des données du Laboratoire Léon Brillouin (LLB, CEA-CNRS)
  • Logiciel pour diffraction sur poudre
• (en) CCP14 : Collaborative Computational Project For Single Crystal and Powder Diffraction
• ICDD (International center for diffraction data, ex-JCPDS : Joint commitee on powder diffraction standards)
  • Denver X-ray conference (DXC)
  • Advances in X-ray Analysis, les minutes de la conférence de Denver
  • Powder diffraction journal (PDJ)
• (en) Fifty Years of X-Ray Diffraction, IUCr
• (en) X-ray's corner
• (en) Australian X-ray Analytical Association (AXAA)
• MacDiff, un logiciel gratuit pour Apple Macintosh
• Fabricants
  • Bruker AXS [1] (anciennement Siemens et Nonius)
  • Diano Corporation
  • General Electric Inspection Technologies (anciennement Seifert)
  • Inel
  • Newport|Micro Controle
  • Oxford Diffraction (anciennement Kuma)
  • PANalytical (anciennement Philips)
  • Rigaku
  • Stoe & Cie GmbH
  • Thermo ARL [2]

Références

• Portail de la chimie
• Portail de la physique