Moindres carrés

Moindres carrés

Méthode des moindres carrés

Illustration de la méthode des moindres carrés. Les données suivent la courbe figurée en pointillés et sont affectées par un bruit gaussien centré, de variance 1. Le meilleur ajustement déterminé par la méthode des moindres carrés est représenté en rouge.

La méthode des moindres carrés, indépendamment élaborée par Legendre en 1805 et Gauss en 1809, permet de comparer des données expérimentales, généralement entachées d’erreurs de mesure à un modèle mathématique censé décrire ces données.

Ce modèle peut prendre diverses formes. Il peut s’agir de lois de conservation que les quantités mesurées doivent respecter. La méthode des moindres carrés permet alors de minimiser l’impact des erreurs expérimentales en « ajoutant de l’information » dans le processus de mesure.

Sommaire

Présentation de la méthode

Dans le cas le plus courant, le modèle théorique est une famille de fonctions ƒ(x;θ) d’une ou plusieurs variables muettes x, indexées par un ou plusieurs paramètres θ inconnus. La méthode des moindres carrés permet de sélectionner parmi ces fonctions, celle qui reproduit le mieux les données expérimentales. On parle dans ce cas d’ajustement par la méthode des moindres carrés. Si les paramètres θ ont un sens physique la procédure d’ajustement donne également une estimation indirecte de la valeur de ces paramètres.

La méthode consiste en une prescription (initialement empirique) qui est que la fonction f(x;θ) qui décrit « le mieux » les données est celle qui minimise la somme quadratique des déviations des mesures aux prédictions de f(x;θ). Si par exemple, nous disposons de N mesures, 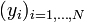(y_i)_{ i = 1,\ldots,N} les paramètres θ « optimaux » au sens de la méthode des moindres carrés sont ceux qui minimisent la quantité :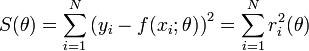

S(\theta) = \sum_{i=1}^N \left(y_i - f(x_i;\theta)\right)^2 = \sum_{i=1}^N r^2_i(\theta)

où les ri(θ) sont les résidus au modèle, i.e. les écarts entre les points de mesure yi et le modèle f(x;θ). S(θ) peut être considéré comme une mesure de la distance entre les données expérimentales et le modèle théorique qui prédit ces données. La prescription des moindres carrés commande que cette distance soit minimale.

Si, comme c'est généralement le cas, on dispose d'une estimation de l'écart-type σi du bruit qui affecte chaque mesure yi, on l'utilise pour « peser » la contribution de la mesure au χ². Une mesure aura d'autant plus de poids que son incertitude sera faible:

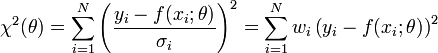
\chi^2(\theta) = \sum_{i=1}^N \left(\frac{y_i - f(x_i;\theta)}{\sigma_i}\right)^2 = \sum_{i=1}^N w_i \left(y_i - f(x_i;\theta)\right)^2

Les quantités wi, inverses des variances des mesures sont appelés poids des mesures. La quantité ci-dessus est appelée khi carré ou khi-deux. Son nom vient de la loi statistique qu'elle décrit, si les erreurs de mesure qui entachent les yi sont distribuées suivant une Loi normale (ce qui est très courant). Dans ce dernier cas, la méthode des moindres carrés permet de plus d’estimer quantitativement l’adéquation du modèle aux mesures, pour peu que l'on dispose d'une estimation fiable des erreurs σi. Si le modèle d’erreur est non gaussien, il faut généralement recourir à la méthode du maximum de vraisemblance, dont la méthode des moindres carrés est un cas particulier.

Son extrême simplicité fait que cette méthode est très couramment utilisée de nos jours en sciences expérimentales. Une application courante est le lissage des données expérimentales par une fonction empirique (fonction linéaire, polynômes ou splines). Cependant son usage le plus important est probablement la mesure de quantités physiques à partir de données expérimentales. Dans de nombreux cas, la quantité que l’on cherche à mesurer n’est pas observable et n’apparaît qu’indirectement comme paramètre θ d’un modèle théorique f(x;θ). Dans ce dernier cas de figure, il est possible de montrer que la méthode des moindres carrés permet de construire un estimateur de θ, qui vérifie certaines conditions d’optimalité. En particulier, lorsque le modèle f(x;θ) est linéaire en fonction de θ, le Théorème de Gauss-Markov garantit que la méthode des moindres carrés permet d'obtenir l'estimateur non-biaisé le moins dispersé. Lorsque le modèle est une fonction non-linéaire des paramètres θ l'estimateur est généralement biaisé. Par ailleurs, dans tous les cas, les estimateurs obtenus sont extrêmement sensibles aux points aberrants : on traduit ce fait en disant qu’ils sont non robustes. Plusieurs techniques permettent cependant de rendre plus robuste la méthode.

Histoire

Carl Friedrich Gauss.

Le jour du Nouvel An de 1801, l'astronome italien Giuseppe Piazzi a découvert l'astéroïde Cérès. Il a alors pu suivre sa trajectoire durant 40 jours. Durant cette année, plusieurs scientifiques ont tenté de prédire sa trajectoire sur la base des observations de Piazzi (à cette époque, la résolution des équations non linéaires de Kepler de la cinématique est un problème très difficile). La plupart des prédictions furent erronées; et le seul calcul suffisamment précis pour permettre à Zach, un astronome allemand, de localiser à nouveau Cérès à la fin de l'année, fut celui de Carl Friedrich Gauss, alors âgé de 24 ans (il avait déjà réalisé l'élaboration des concepts fondamentaux en 1795, lorsqu'il était alors âgé de 18 ans). Mais sa méthode des moindres carrés ne fut publiée qu'en 1809, lorsqu'elle parut dans le tome 2 de ses travaux sur la Mécanique céleste , Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium. Le mathématicien français Adrien-Marie Legendre a développé indépendamment la même méthode en 1805. Le mathématicien américain Robert Adrain a publié en 1808 une formulation de la méthode.

En 1829, Gauss a pu donner les raisons de l'efficacité de cette méthode ; en effet, la méthode des moindres carrés est justement optimale à l'égard de bien des critères. Cet argument est maintenant connu sous le nom du théorème de Gauss-Markov.

Formalisme

Deux exemples simples

Moyenne d'une série de mesures indépendantes

L'exemple le plus simple d'ajustement par la méthode des moindres carrés est probablement le calcul de la moyenne m d'un ensemble de mesures indépendantes (yi)i = 1..N entachées d'erreurs gaussiennes. Autrement dit, on veut estimer m dans la relation

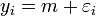
y_i = m + \varepsilon_i

pour i = 1,..,N et où \varepsilon est un bruit blanc.

La prescription des moindres carrés revient à minimiser la quantité :

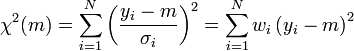
\chi^2(m) = \sum_{i=1}^N \left(\frac{y_i -m}{\sigma_i}\right)^2 = \sum_{i=1}^N w_i \left(y_i - m\right)^2

où les 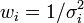w_i = 1 / \sigma_i^2 sont les poids des mesures yi. Statistiquement, les 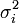\sigma_i^2 s'interprètent comme la variance de la variable aléatoire 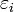\varepsilon_i. On parle alors de moindres carrés pondérés (en anglais, le sigle est GLS). Lorsqu'on ne tient pas compte de la pondération, on pose simplement wi = 1 et on parle de moindres carrés ordinaires (MCO) (sigle anglais: OLS).

La quantité χ2(m), ou somme des carrés des résidus, est une forme quadratique définie positive. Son minimum se calcule par différenciation : gradχ2(m) = 0. Cela donne la formule classique :

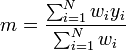
m = \frac{\sum_{i=1}^N w_i y_i}{\sum_{i=1}^N w_i}

Autrement dit, l'estimateur par moindres carrés de la moyenne m d'une série de mesures entachées d'erreurs gaussiennes (connues) est leur moyenne pesée (ou pondérée), c'est-à-dire leur moyenne empirique dans laquelle chaque mesure est pondérée par l'inverse du carré de son incertitude. Le Théorème de Gauss-Markov garantit qu'il s'agit du meilleur estimateur linéaire non-biaisé de m.


La moyenne estimée m fluctue en fonction des séries de mesures yi effectuées. Comme chaque mesure est affectée d'une erreur aléatoire, on concoit que la moyenne d'une première série de N mesures diffèrera de la moyenne d'une seconde série de N mesures, même si celles-ci sont réalisées dans des conditions identiques. Il importe de pouvoir quantifier l'amplitude de telles fluctuations, car cela détermine la precision de la détermination de la moyenne m. Chaque mesure yi peut être considérée comme une réalisation d'une variable aléatoire Yi, de moyenne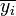 \overline{y_i} et de d'écart-type σi. L'estimateur de la moyenne obtenu par la méthode des moindres carrés, combinaison linéaire de variables aléatoires, est lui-même une variable aléatoire :

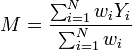M = \frac{\sum_{i=1}^N w_i Y_i}{\sum_{i=1}^N w_i} .

L'écart-type des fluctuations de M est donné par (combinaison linéaire de variables aléatoires indépendantes):

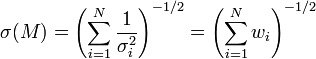
\sigma(M) = \left(\sum_{i=1}^N \frac{1}{\sigma_i^2}\right)^{-1/2} = \left(\sum_{i=1}^N w_i\right)^{-1/2}

Sans grande surprise, la précision de la moyenne d'une série de N mesures est donc déterminée par le nombre de mesures, et la précision de chacune de ces mesures. Dans le cas où chaque mesure est affectée de la même incertitude σi = σ la formule précédente se simplifie en :

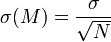
\sigma(M) = \frac{\sigma}{\sqrt{N}}

La précision de la moyenne s'accroit donc comme la racine carrée du nombre de mesures. Par exemple, pour doubler la précision, il faut quatre fois plus de données ; pour la multiplier par 10, il faut 100 fois plus de données.

Régression linéaire

Article détaillé : Régression linéaire.
Ajustement d'un modèle de type y = a * x + b par la méthode des moindres carrés. Les données suivent la loi figurée en pointillés et sont affectées d'erreurs gaussiennes, de variance 1. L'ajustement déterminé (courbe rouge) est le meilleur estimateur de la pente et de l'ordonnée à l'origine compte tenu de la quantité d'information contenu dans les points de mesure.

Un autre exemple est l'ajustement d'une loi linéaire du type 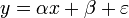y=\alpha x + \beta + \varepsilon sur des mesures indépendantes, fonction d'un paramètre connu x. Le terme \varepsilon permet de prendre en compte des erreurs de mesure. Lorsque on ajoute d'autres explicatives (k variables x), on gagnera à adopter la notation matricielle:

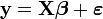
\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}

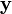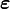où les vecteurs \mathbf{y} et \boldsymbol{\varepsilon} sont de dimension n × 1, la matrice 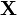\mathbf{X} n × k et 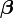\boldsymbol{\beta} de dimension k × 1.

L'utilisation de la régression linéaire se rencontre par exemple lorsque l'on veut calibrer un appareil de mesure simple (ampèremètre, thermomètre) dont le fonctionnement est linéaire. y est alors la mesure instrumentale (déviation d'une aiguille, nombre de pas d'un ADC, ...) et x la grandeur physique qu'est censé mesurer l'appareil, généralement mieux connue, si l'on utilise une source de calibration fiable. La méthode des moindres carrés permet alors de mesurer la loi de calibration de l'appareil, d'estimer l'adéquation de cette loi aux mesures de calibration (i.e. dans le cas présent, la linéarité de l'appareil) et de propager les erreurs de calibration aux futures mesures effectuées avec l'appareil calibré. En général, les erreurs (et les corrélations) portant sur les mesures yi et les mesures xi doivent être prises en compte. Ce cas sera traité dans la section suivante.

La prescription des moindres carrés s'écrit pour ce type de modèle:


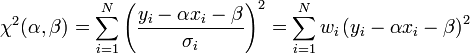
\chi^2(\alpha, \beta) = \sum_{i=1}^N \left( \frac{y_i - \alpha x_i - \beta}{\sigma_i} \right)^2 = \sum_{i=1}^N w_i \left(y_i - \alpha x_i - \beta \right)^2


Le minimum de cette somme des carrés pondérés est atteint pour gradχ2 = 0, ce qui donne: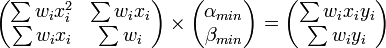


\begin{pmatrix} \sum w_i x_i^2 & \sum w_i x_i \\ \sum w_i x_i & \sum w_i \\ \end{pmatrix} \times \begin{pmatrix} \alpha_{min} \\ \beta_{min} \\ \end{pmatrix} = \begin{pmatrix} \sum w_i x_i y_i \\ \sum w_i y_i \\ \end{pmatrix}

ou, plus explicitement:

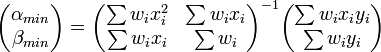
\begin{pmatrix} \alpha_{min} \\ \beta_{min} \\ \end{pmatrix} = \begin{pmatrix} \sum w_i x_i^2 & \sum w_i x_i \\ \sum w_i x_i & \sum w_i \\ \end{pmatrix}^{-1} \begin{pmatrix} \sum w_i x_i y_i \\ \sum w_i y_i \\ \end{pmatrix}

Là encore, il s'agit d'une estimation par moindre carré généralisé ou pondéré (GLS). La détermination des paramètres "optimaux" (au sens des moindres carrés) α et β se ramène donc à la résolution d'un système d'équations linéaires. Il s'agit là d'une propriété très intéressante, liée au fait que le modèle lui-même est linéaire. On parle d'ajustement ou de régression linéaire. Dans le cas général, la détermination du minimum du χ2 est un problème plus compliqué, et généralement coûteux en temps de calcul (cf. sections suivantes).


La valeur des paramètres αmin et βmin dépend des mesures yi réalisées. Comme ces mesures sont entachées d'erreur, on conçoit bien que si l'on répète M fois les N mesures de calibration, et que l'on réalise à l'issue de chaque série l'ajustement décrit plus haut, on obtiendra M valeurs numériquement différentes de αmin et βmin. Les paramètres de l'ajustement peuvent donc être considérés comme des variables aléatoires, dont la loi est fonction du modèle ajusté et de la loi des yi.

En particulier, l'espérance du vecteur (αmin;βmin) est le vecteur des vraies valeurs des paramètres: l'estimation est donc sans-biais. Qui plus est, on montre que la dispersion qui affecte les valeurs de αmin et βmin dépend du nombre de points de mesure, N, et de la dispersion qui affecte les mesures (moins les mesures sont précises, plus αmin et βmin fluctueront). Par ailleurs, αmin et βmin ne sont généralement pas des variables indépendantes. Elles sont généralement corrélées, et leur corrélation dépend du modèle ajusté (nous avons supposé les yi indépendants).

Ajustement d'un modèle linéaire quelconque

Un modèle y = f(x;θ) est linéaire, si sa dépendance en θ est linéaire. Un tel modèle s'écrit :

y= f(x;\theta) = \sum_{k=1}^n \theta_k \phi_k(x)

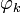où les \varphi_k sont n fonctions quelconques de la variable x. Un tel cas est très courant en pratique: les deux modèles étudiés plus haut sont linéaires. Plus généralement tout modèle polynomial est linèaire, avec φk(x) = xk. Enfin, de très nombreux modèles utilisés en sciences expérimentales sont des développement sur des bases fonctionnelles classiques (splines, base de Fourier, bases d'ondelettes etc.)

Si nous disposons de N mesures, (xi,yi,σi), le χ2 peut être écrit sous la forme :

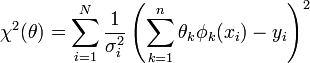
\chi^2(\mathbf{\theta}) = \sum_{i=1}^N \frac{1}{\sigma_i^2} \left(\sum_{k=1}^n \theta_k \phi_k(x_i) -y_i \right)^2

Nous pouvons exploiter la linéarité du modèle pour exprimer le χ2 sous une forme matricielle plus simple. En effet, en définissant :

\mathbf{J} = \begin{pmatrix} \phi_1(x_1) & \ldots & \phi_n(x_1) \\ \vdots & & \vdots \\ \phi_1(x_N) & \ldots & \phi_n(x_N) \\ \end{pmatrix}
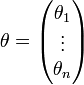
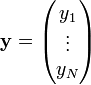
\mathbf{\theta} = \begin{pmatrix} \theta_1 \\ \vdots \\ \theta_n \\ \end{pmatrix}
\mathbf{y} = \begin{pmatrix} y_1 \\ \vdots \\ y_N \\ \end{pmatrix}

et

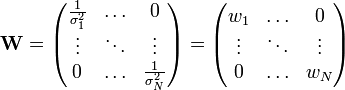
\mathbf{W} = \begin{pmatrix} \frac{1}{\sigma_1^2} & \ldots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \ldots & \frac{1}{\sigma_N^2}\\ \end{pmatrix} = \begin{pmatrix} w_1 & \ldots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \ldots & w_N \\ \end{pmatrix}

on montre facilement que le χ2 s'écrit sous la forme:

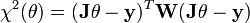
\chi^2(\mathbf{\theta}) = (\mathbf{J\theta} - \mathbf{y})^T \mathbf{W} (\mathbf{J\theta} - \mathbf{y})

La matrice J est appelée matrice jacobienne du problème. C'est une matrice rectangulaire, de dimension N x n, avec généralement N >> n. Elle contient les valeurs des fonctions de base φk pour chaque point de mesure. La matrice diagonale W est appelée matrice des poids. C'est l'inverse de la matrice de covariance des yi. On montre que si les yi sont corrélés, la relation ci-dessus est toujours valable. W n'est simplement plus diagonale, car les covariances entre les yi ne sont plus nulles.

En différentiant la relation ci-dessus par rapport à chaque θk, on obtient :

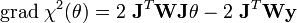
{\rm grad}\ \chi^2(\mathbf{\theta}) = 2\ \mathbf{J}^T \mathbf{W J \theta} - 2\ \mathbf{J}^T \mathbf{Wy}

et le minimum du χ2 est dont atteint pour θmin égal à :

\theta_{min} = \left(\mathbf{J}^T \mathbf{WJ}\right)^{-1}\ \mathbf{J}^T \mathbf{Wy}

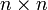On retrouve la propriété remarquable des problèmes linéaires, qui est que le modèle optimal peut-être obtenu en une seule operation, à savoir la résolution d'un système n \times n .

Équations normales

Dans le cas d'équations linéaires surdéterminées à coefficients constants, il existe une solution simple[1]. Si nous supposons que nous disposons d'équation expérimentales surdéterminée </ref>

A \vec x = \vec b

Nous allons représenter l'erreur commise par un vecteur résidu

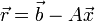
\vec r = \vec b - A \vec x

La norme du résidu 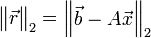\begin{Vmatrix} \vec r \end{Vmatrix}_2 = \begin{Vmatrix} \vec b- A \vec x\end{Vmatrix}_2 est minimum si et seulement si 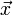\vec x satisfait les équations normales :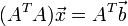

(A^T A) \vec x = A^T \vec b

Ajustement de modèles non-linéaires

Article détaillé : moindres carrés non linéaires.

Dans de nombreux cas, la dépendance du modèle en θ est non-linéaire. Par exemple, si f(x;θ) = f(x;(A,ω,φ)) = Acos(ωx + φ), ou f(x;θ) = f(x;τ) = exp( − x / τ). Dans ce cas, le formalisme décrit à la section précédente ne peut pas être appliqué directement. L'approche généralement employée consiste alors à partir d'une estimation de la solution, à linéariser le χ2 en ce point, résoudre le problème linéarisé, puis itérer. Cette approche est équivalente à l'algorithme de minimisation de Gauss-Newton. D'autres techniques de minimisation existent. Certaines comme l'Algorithme de Levenberg-Marquardt, sont des raffinements de l'algorithme de Gauss-Newton. D'autres sont applicables lorsque les dérivées du χ2 sont difficiles ou coûteuses à calculer.

Une des difficultés des problèmes de moindres carrés non-linéaires est l'existence fréquente de plusieurs minima locaux. Une exploration systématique de l'espace des paramètres peut alors se révéler nécessaire.

Ajustement sous contraintes

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Ajustement de modèles implicites

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Interprétation statistique

Estimation statistique

Modèle standard: moindres carrés ordinaires

Pour le modèle matriciel

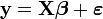
\mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}

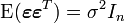on conserve les hypothèses conventionnelles que \operatorname{E}(\boldsymbol{\varepsilon})=\mathbf{0} et que \operatorname{E} (\boldsymbol{\varepsilon} \boldsymbol{\varepsilon}^T) = \sigma^2 I_n, où In est la matrice d'identité. Dans ce cas, l'estimateur par moindre carré ordinaire (MCO) est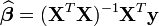

\boldsymbol{\widehat{\beta}} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}

Une formalisation supplémentaire (on suppose par exemple en plus que les aléas sont normaux) permet d'obtenir les propriétés asymptotiques de l'estimateur:

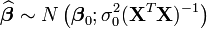
\boldsymbol{\widehat{\beta}} \sim N \left(\boldsymbol{\beta}_0 ; \sigma_0^2 (\mathbf{X}^T \mathbf{X})^{-1} \right)

Les indices 0 indiquent qu'il s'agit de la vraie valeur des paramètres.

Moindres carrés généralisés

Lorsqu'on relâche (un peu) l'hypothèse sur la structure de la matrice de variance-covariance des erreurs, on peut toujours obtenir un estimateur par moindre-carré. On suppose donc que 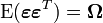\operatorname{E} (\boldsymbol{\varepsilon} \boldsymbol{\varepsilon}^T) = \boldsymbol{\Omega}, où cette dernière matrice est connue. L'estimateur par moindre carré (dit par moindre carré généralisé, GLS) s'écrit toujours: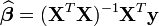

\boldsymbol{\widehat{\beta}} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}

Les propriétés asymptotiques changent par rapport au cas standard:

\boldsymbol{\widehat{\beta}} \sim N \left(\boldsymbol{\beta}_0 ; (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \boldsymbol{\Omega} \mathbf{X} (\mathbf{X}^T \mathbf{X})^{-1}\right)

Soit:

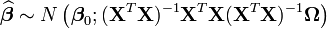
\boldsymbol{\widehat{\beta}} \sim N \left(\boldsymbol{\beta}_0 ; (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{X} (\mathbf{X}^T \mathbf{X})^{-1} \boldsymbol{\Omega}\right)
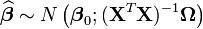
\boldsymbol{\widehat{\beta}} \sim N \left(\boldsymbol{\beta}_0 ; (\mathbf{X}^T \mathbf{X})^{-1} \boldsymbol{\Omega}\right)

Cela influence bien sûr les procédures de test dans le modèle linéaire.

Moindres carrés pondérés

Si l'on connaît parfaitement la matrice de variance-covariance 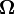\boldsymbol{\Omega}, on peut considérer la méthode des moindres carrés pondérés. Pour cela, on considère la décomposition de Cholesky de cette matrice: 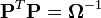\mathbf{P}^T \mathbf{P} = \boldsymbol{\Omega}^{-1} et on prémultiplie chaque membre de la régression par 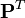\mathbf{P}^T, pour obtenir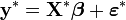

\mathbf{y}^\ast = \mathbf{X}^\ast \boldsymbol{\beta} + \boldsymbol{\varepsilon}^\ast

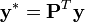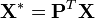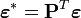avec \mathbf{y}^\ast = \mathbf{P}^T\mathbf{y}, \mathbf{X}^\ast = \mathbf{P}^T\mathbf{X} et \boldsymbol{\varepsilon}^\ast = \mathbf{P}^T \boldsymbol{\varepsilon}. Ainsi transformé, ce modèle vérifie toutes les hypothèses requises par les MCO et l'estimateur en résultant présentera toutes les bonnes propriétés (notamment du point de vue de la matrice de variance-covariance):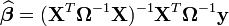

\boldsymbol{\widehat{\beta}} = (\mathbf{X}^T \boldsymbol{\Omega}^{-1} \mathbf{X})^{-1} \mathbf{X}^T \boldsymbol{\Omega}^{-1}\mathbf{y}

La distribution asymptotique sera:

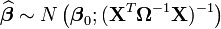
\boldsymbol{\widehat{\beta}} \sim N \left(\boldsymbol{\beta}_0 ; (\mathbf{X}^T \boldsymbol{\Omega}^{-1} \mathbf{X})^{-1}\right)

Soit:

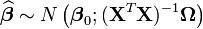
\boldsymbol{\widehat{\beta}} \sim N \left(\boldsymbol{\beta}_0 ; (\mathbf{X}^T \mathbf{X})^{-1} \boldsymbol{\Omega}\right)

Le critère du χ²

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Optimalité de la méthode des moindres carrés

Dans la régression linéaire classique,

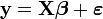
\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}

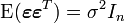On suppose généralement que \operatorname{E}(\boldsymbol{\varepsilon})=\mathbf{0} et que \operatorname{E} (\boldsymbol{\varepsilon} \boldsymbol{\varepsilon}^T) = \sigma^2 I_n, où In est la matrice d'identité. La dernière hypothèse porte sur la structure de variance-covariance des aléas: on suppose que pour tout i, 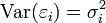\operatorname{Var}(\varepsilon_i) = \sigma^2_i (homoscédasticité) et que 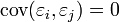\operatorname{cov}(\varepsilon_i,\varepsilon_j) = 0 pour i \neq j (indépendance).

L'estimation par moindres carrés ordinaires (MCO) est

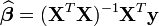
\boldsymbol{\widehat{\beta}} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}

Sous les hypothèses précédentes, cet estimateur est connu pour être le meilleur estimateur linéaire sans biais (voir le Théorème de Gauss-Markov): cela signifie que parmi les estimateurs du type 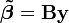\boldsymbol{\tilde{\beta}} = \mathbf{B} \mathbf{y} non biaisé, l'estimateur MCO présente une variance minimale.

Enfin, si on suppose de plus que les aléas sont gaussiens, le modèle peut s'estimer par la Maximum de vraisemblance . Cet estimateur se trouve être celui par moindre carré MCO et atteignant la borne de Cramer-Rao.

Enfin, sous les hypothèses du paragraphe sur les moindres carrés généralisés, l'estimateur reste BLUE.

Robustesse

Sensibilité aux points aberrants

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Techniques de robustification

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Articles connexes

Logiciel

  • lmfit minimisation selon l'algorithme de Levenberg-Marquardt, pour utilisation dans des programmes en C ou C++.

Références

  1. ↑ "3.6 système surdéterminé" dans Analyse numérique première partie, Professeur F.X. LITT, Centrale des cours de l'AEES (ULg)
  • Portail des probabilités et des statistiques Portail des probabilités et des statistiques

Ce document provient de « M%C3%A9thode des moindres carr%C3%A9s ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Moindres carrés de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Moindres carrés non linéaires — Les moindres carrés non linéaires est une forme des moindres carrés spécialisée dans l estimation d un modèle non linéaire en n paramètres à partir de m observations (m > n). Une façon d estimer ce genre de problème est de considérer …   Wikipédia en Français

  • Méthode des moindres carrés — Illustration de la méthode des moindres carrés. Les données suivent la courbe figurée en pointillés et sont affectées par un bruit gaussien centré, de variance 1. Le meilleur ajustement déterminé par la méthode des moindres carrés est représenté… …   Wikipédia en Français

  • Methode des moindres carres — Méthode des moindres carrés Illustration de la méthode des moindres carrés. Les données suivent la courbe figurée en pointillés et sont affectées par un bruit gaussien centré, de variance 1. Le meilleur ajustement déterminé par la méthode des… …   Wikipédia en Français

  • Méthode Des Moindres Carrés — Illustration de la méthode des moindres carrés. Les données suivent la courbe figurée en pointillés et sont affectées par un bruit gaussien centré, de variance 1. Le meilleur ajustement déterminé par la méthode des moindres carrés est représenté… …   Wikipédia en Français

  • Méthode des doubles moindres carrés — La méthode des doubles moindres carrés (DMC) ou la méthode moindres carrés en deux étapes est une méthode utilisée en économétrie introduit par Robert Basmann en 1957 et Henri Theil en 1961. Voir aussi Articles connexes Méthode des moindres… …   Wikipédia en Français

  • Algorithme des moindres carrés récursifs — L algorithmique des moindres carrés récursifs (en anglais, RLS ou Recursive least squares) est un algorithme de filtre adaptatif utilisé en traitement numérique du signal. Il fournit une manière récursive pour calculer le filtre qui minimise une… …   Wikipédia en Français

  • méthode des moindres carrés — minimaliųjų kvadratų metodas statusas T sritis automatika atitikmenys: angl. least squares method; method of least squares vok. Methode der kleinsten Quadrate, f rus. метод наименьших квадратов, m pranc. méthode de plus petits carrés, f; méthode… …   Automatikos terminų žodynas

  • Méthode des moindres carrés ordinaire — La méthode des moindres carrés ordinaire (MCO) est le nom technique de la régression mathématique en statistiques, et plus particulièrement de la régression linéaire. Il s agit d ajuster un nuage de points {Yi,Xi}i = 1,...,n selon une relation… …   Wikipédia en Français

  • approximation des moindres carrés — aproksimacija minimaliųjų kvadratų metodu statusas T sritis automatika atitikmenys: angl. least squares approximation vok. Approximation durch kleinste Quadrate, f rus. аппроксимация методом наименьших квадратов, f pranc. approximation des… …   Automatikos terminų žodynas

  • méthode des moindres carrés — mažiausiųjų kvadratų metodas statusas T sritis Standartizacija ir metrologija apibrėžtis Metodas, kuriuo randami skirstinio nežinomųjų parametrų statistiniai įverčiai. atitikmenys: angl. least squares method; method of least squares vok.… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”