Diffractometre

Le diffractomètre est un appareil permettant de mesurer la diffraction d'une onde sur une cible. Le terme est utilisé exclusivement pour la diffractométrie de rayons X.

Les premiers diffractomètres utilisaient une pellicule argentique qui était impressionnée par les rayons X. C'étaient parfois juste un tube, un porte-échantillon et un porte-film posés sur une table (les dangers des rayons X étaient sous-estimés à l'époque), parfois mis dans une « boîte ». Il portait de ce fait le nom de « chambre », les Britanniques parlant de « camera ».

Sommaire 1 Sources de rayons X 2 Chambre de Laue 3 Chambre de Debye-Scherrer 4 Autres chambres 5 Diffractomètre de poudres 5.1 Montage à deux cercles 5.2 Géométrie Bragg-Brentano 5.3 Autres géométries 5.3.1 Incidence rasante 5.3.2 Mesure en bercement 5.3.3 Faisceau parallèle 5.4 Optique 5.5 Porte-échantillon 5.6 Détecteurs 6 Diffractomètre de monocristal 6.1 La réception du signal 7 Voir aussi 7.1 Bibliographie 7.2 Liens internes 7.3 Liens externes 7.4 Référence

Sources de rayons X

La première source de rayons X fut la désintégration radioactive. Cette source est encore parfois utilisée en spectrométrie de fluorescence X, mais plus en diffraction.

En général, les rayons X sont produits par freinage des électrons. On utilise en général des tubes à rayons X, dispositifs de petite taille (environ 50 cm de long pour une dizaine de cm de diamètre, plus pour les tubes à anode tournante). Dans la plupart des cas, on modifie le spectre du tube afin de s'approcher des conditions monochromatiques :

• soit avec un filtre de nickel pour « couper » la raie Kβ dans le cas d'un tube au cuivre ;
• soit avec un monochromateur (système diffractant sélectionnant la raie Kα₁).

Les diffractomètres sont également placés dans des lignes de faisceau synchrotron. Le rayonnement synchrotron permet d'avoir des rayons X monochromatiques et parfaitement collimatés, ce qui permet des mesures très précises. Cependant, un synchrotron est une installation de plusieurs centaines de mètres de diamètre et de coût de structure faramineux, ce qui réserve son utilisation aux cas vraiment nécessaires.

Chambre de Laue

La chambre de Laue est le dispositif le plus simple pour faire un cliché de diffraction, mais il n'est adapté qu'aux monocristaux.

Il consiste en un tube de rayons X émettant sur un spectre large (spectre polychromatique), un porte-échantillon, et un support de film photographique. Le film photographique est masqué par un papier afin de ne pas être voilé par la lumière ; les rayons X seuls traversent le papier et impressionnent le film.

Le cliché obtenu permet de déterminer les paramètres de maille du cristal ainsi que l'orientation du réseau par rapport à la face analysée. Il est similaire au cliché de diffraction obtenu en microscopie électronique en transmission.

Lorsque l'on veut faire des mesures plus précises, on utilise un diffractomètre muni d'un goniomètre à trois cercles permettant d'orienter le monocristal (en général un nanocristal), le film étant remplacé par un détecteur à deux dimensions (type caméra CCD ou chambre à fils), voir plus bas. On peut ainsi acquérir plusieurs clichés de Laue de manière automatisée.

Chambre de Debye-Scherrer

La chambre de Debye-Scherrer est le dispositif le plus simple permettant de faire de la diffraction sur poudre ou sur échantillon polycristallin.

Il se compose d'une source monochromatique de rayons X, d'un porte-échantillon et d'un film en forme de bande qui entoure le dispositif. Les rayons X sont diffractés sous la forme de cônes, qui laissent des traces en forme de cercle sur la bande.

On voit parfois le terme « caméra de Debye-Scherrer », mais il semble que ce soit un anglicisme, il est en effet peu utilisé en français. Le terme est toutefois correct sur le plan étymologique, le mot latin camera signifiant « chambre », et l'analogie avec la caméra de cinéma est pertinente (chambre noire servant à impressionner un film photographique), bien que dans le cas des rayons X il n'y ait pas de mouvement.

Ce dispositif est très simple et peu coûteux, mais s'il permet de localiser aisément la position des pics (rayon de l'arc de cercle sur la bande), la trace photographique rend peu précise l'estimation de l'intensité (niveau de gris) et la largeur du pic (largeur de l'arc).

Les autres sources d'incertitude sont :

• absorption de l'échantillon,
• taille de l'échantillon, qui est limitée à une dizaine de milligrammes, moins d'un millimètre de diamètre,
• problèmes de centrage,
• stabilité du film (par exemple variations de dimension, retrait).

Initialement, le dépouillement des données était fait manuellement, la position des arcs étant repérée avec une règle. La numérisation des films (avec un scanneur) permet un traitement informatique du diffractogramme.

On trouve également des chambres Debye-Scherrer où le film est remplacé par une série de détecteurs placés en arc de cercle autour de l'échantillon, offrant une résolution de l'ordre du centième de degré. Ce dispositif permet une acquisition directe sur ordinateur, avec une mesure précise des intensités (nombre de coups reçus par chaque détecteur).

Ce dispositif a été de fait quasiment systématiquement remplacé par un diffractomètre de poudre « mécanisé » (avec un détecteur ponctuel mobile monté sur un goniomètre à deux cercles). Ces diffractomètres à goniomètre sont prévus pour une géométrie Bragg-Brentano, mais ils peuvent être utilisés en géométrie Debye-Scherrer, par exemple lorsque l'on a peu de produit : la poudre est introduite dans un capillaire, on travaille avec un faisceau parallèle, et le détecteur fait le tour de l'échantillon.

Autres chambres

Chambre de Guinier

Chambre de Gandolfi

Chambre de Seeman-Bohlin

Diffractomètre de poudres

Un diffractomètre de poudres est un diffractomètre à bras mobiles. Les premiers modèles étaient mus par des manivelles, puis sont venus les bras motorisés ; les diffractomètres modernes sont entièrement automatisés et commandés par ordinateur.

Montage à deux cercles

Dans le cas général, l'appareil possède un goniomètre « à deux cercles », c'est-à-dire ne permettant de faire varier que deux angles : l'angle d'incidence des rayons X sur l'échantillon γ, et l'angle de déviation 2θ. Ceci peut être réalisé par deux montages, dits « θ-2θ » (thêta-deux thêta) et « θ-θ » (thêta-thêta). Dans les deux cas, le détecteur est mobile, c'est sa position qui détermine la déviation 2θ ; la différence est dans la détermination de l'incidence γ :

• montage θ-2θ : le tube à rayons X est fixe , le porte-échantillon est motorisé ; le tube étant la partie la plus lourde, ce montage est le plus simple d'un point de vue mécanique ;
  son nom vient du fait qu'en géométrie Bragg-Brentano (voir ci-dessous), l'angle que parcourt le porte-échantillon par rapport à la déviation 0 vaut ½·2θ = θ, tandis que le détecteur parcourt un angle 2θ ;
• montage θ-θ (thêta-thêta) : le porte-échantillon est fixe, le tube est mobile ; l'avantage de ce montage est que le porte-échantillon reste horizontal, ce qui empêche la poudre de s'écouler et facilite le montage d'un dispositif autour du porte-échantillon, comme un four ou une chambre à atmosphère contrôlée ;
  son nom vient du fait qu'en géométrie Bragg-Brentano (voir ci-dessous), le tube et le détecteur sont chacun situés à l'angle θ par rapport à la surface de l'échantillon, de part et d'autre de la perpendiculaire à cette surface.

Les diffractomètres de ce type sont les plus versatiles, on peut en effet faire varier la géométrie et faire :

• des mesures en bercement (rocking curves) : l'angle de déviation reste fixe, seul change l'angle d'incidence ;
  • sur un appareil θ-2θ, le détecteur est fixe et le porte-échantillon bouge ;
  • sur un appareil θ-θ, le tube et le détecteur bougent ensemble ;
• de type Debye-Scherrer : le porte-échantillon est un fin tube de verre (un capillaire), et l'angle d'incidence est fixe, seul varie la position du détecteur (balayage en 2θ, ou 2θ scan).

Géométrie Bragg-Brentano

La géométrie de Bragg-Brentano consiste à avoir une focalisation approchée des rayons X (parfois appelée « parafocalisation », en anglais parafocussing).

L'idée est d'éclairer l'échantillon avec un faisceau divergent, ce qui permet d'avoir plus d'intensité qu'avec un faisceau fin. Ce faisant, on introduit une erreur angulaire, les rayons X ne frappant pas l'échantillon avec le même angle. Ce défaut est corrigé de deux manières :

• d'une part en travaillant avec des échantillons polycristallins (pulvérulents ou massifs) isotropes, c'est-à-dire sans orientation cristalline préférentielle ;
• d'autre part en s'assurant que le détecteur est toujours symétrique au tube par rapport à l'échantillon, c'est-à-dire en fixant γ = ½·2θ ; ainsi, la géométrie du cercle fait que les rayons qui convergent vers le détecteur ont presque tous subi la même déviation.

Comme il s'agit d'une méthode sur poudre, on travaille avec une source monochromatique et un détecteur ponctuel. On peut remplacer le détecteur ponctuel par un détecteur linéaire ou à deux dimensions, afin d'accélérer la mesure. Cependant, on n'est plus strictement en géométrie Bragg-Brentano, même si les résultats sont similaires.

Autres géométries

Les diffractomètres de poudre peuvent s'utiliser avec une autre géométrie que la géométrie de Bragg-Brentano.

Incidence rasante

Les mesures en incidence rasante se font à incidence γ fixe, et en faisant varier 2θ. On fait en général des mesures pour plusieurs valeurs de γ. Pour éviter que des rayons X passent par dessus l'échantillon et frappent directement le détecteur aux faibles angles, on utilise un faisceau fin et on peut placer un « couteau » (écran métallique) au-dessus de l'échantillon.

L'absorption des rayons X dépend du trajet dans l'échantillon (cf. loi de Beer-Lambert). Au-delà d'une certaine distance d parcourue, les rayons sont trop absorbés et ne contribuent quasiment pas au signal ; cette distance d choisie par convention est celle donnant 90 % du signal.

Le rayon incident parcourt une distance x₁ valant e/sin(γ) pour atteindre une profondeur e, et une distance x₂ valant e/sin(2θ-γ) pour ressortir et frapper le détecteur. La couche d'atomes située à une profondeur e contribue donc de manière significative au signal uniquement si

x₁ + x₂ < d

soit

.

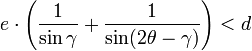Dans le cas d'un échantillon bicouche, l'angle d'incidence γ à partir duquel on peut détecter un pic du substrat permet de déterminer l'épaisseur de la couche située au-dessus.

Mesure en bercement

Les mesures en bercement ou en balancement (rocking curves en anglais), consistent à faire varier l'angle d'incidence γ tout en maintenant la déviation 2θ constante. En raison de la défocalisation, il faut travailler avec un faisceau fin. On fait en général plusieurs mesures sur un intervalle de γ donné, mais en faisant varier 2θ entre chaque mesure.

Ces mesures en général sont utilisées pour déterminer l'orientation d'une couche épitaxiée ; par exemple, dans l'industrie des semi-conducteurs, on fait croître une couche cristalline sur un monocristal de silicium. On effectue des mesures pour une plage de 2θ couvrant un pic du substrat et un pic de la couche. Les deux pics sont maximaux pour des valeurs de γ différentes, et ceci donne la désorientation entre le substrat et la couche.

Faisceau parallèle

Une géométrie en faisceau parallèle permet de s'affranchir de la forme de l'échantillon. En effet, en faisceau divergent, la surface de l'échantillon doit être tangente au cercle de focalisation pour que l'on puisse faire l'hypothèse que tous les rayons frappant le détecteur subissent la même déviation. Si le faisceau est parallèle, alors la déviation ne dépend que de la direction du détecteur.

On utilise pour cela un système diffractant courbé (ce n'est donc pas à proprement parler un miroir), et dont la courbe est un arc de parabole. Le centre du tube (la ligne de l'anti-cathode sur laquelle se projettent les électrons) est placée au foyer de cette parabole. L'alignement du miroir est sans doute l'opération qui conditionne le plus la qualité de la mesure.

Cette méthode a été développée par H. Göbel^[1], le système diffractant porte donc le nom de « miroir de Göbel » (ou « miroir de Goebel », voir l'article Umlaut).

Le miroir de Göbel n'est utile qu'avec un monochromateur arrière. Sinon, la technique ne présente aucun avantage.

Ce système est par exemple utilisé lorsque l'on dispose d'extrêmement peu de matière. La poudre est introduite dans un capillaire (tube de verre très fin), et on réalise un balayage avec le détecteur (c'est en fait en quelque sorte la méthode de Debye-Scherrer mais avec un détecteur électronique au lieu d'un film photographique). Le faisceau parallèle peut également être utilisé pour une mesure sur une pièce non plane (courbe, rugueuse), voir pour une mesure non destructrice (on place une pièce entière, par exemple un objet d'art, dans l'appareil).

Le miroir est un multicouche de synthèse. La principale limitation de sa durée de vie est l'oxydation des couches, en particulier par l'ozone que peut produire la haute tension du tube. Pour éviter ceci, les miroirs de Göbel sont sous atmosphère inerte, dans un boîtier muni de fenêtres transparentes aux rayons X.

Optique

Dans la configuration Bragg-Brentano, les rayons X ont une divergence radiale, la configuration permettant la focalisation approchée. C'est donc une bande rectangulaire de l'échantillon qui est éclairée. La divergence radiale est limitée par une fente rectangulaire située entre le tube et l'échantillon, appelée « fente primaire », « fente avant » ou « fente de divergence ». Une autre fente se trouve devant le détecteur, elle limite le volume que « voit » le détecteur à la seule zone irradiée de l'échantillon ; cette fente porte le nom de « fente secondaire », « fente arrière » ou « fente anti-diffusion ». Ces fentes déterminent l'intensité qui atteint le détecteur ainsi que le bruit de fond.

Les rayons X ont également une divergence axiale. On essaie en général de limiter cette divergence axiale par des « fentes de Soller », parfois appelées « collimateurs » : il s'agit de lames de cuivre parallèles, qui absorbent les rayons qui ne sont pas parallèles aux lames. La divergence est limitée à quelques degrés (en général, entre 0,1 et 5°). Plus la divergence est étroite, plus les pics de diffraction sont étroits, mais plus l'intensité est faible. Sans fente de Soller, on a des pics larges et dissymétriques.

Porte-échantillon

Dans le cas le plus simple, le porte-échantillon est une simple pièce passive soit fixe (montage θ-θ), soit motorisée (montage θ-2θ). Il permet en général de faire tourner l'échantillon dans son plan (spinner) ; en effet, comme seule une petite portion de l'échantillon est éclairée (un rectangle étroit), le fait de faire tourner l'échantillon permet de balayer un disque, le signal collecté représente donc une plus grande surface d'échantillon. Ceci permet d'englober plus de cristallites, et donc d'avoir une meilleure représentation statistique.

Le porte-échantillon peut également être un passeur : on charge plusieurs échantillons, et ceux-ci sont mesurés successivement, ce qui permet de mesurer plusieurs échantillons sans avoir besoin d'intervenir pour les changer (par exemple mesure de nuit). Dans certains cas, le passeur est distinct du porte-échantillon, il amène l'échantillon au porte-échantillon ; on peut par exemple avoir une mesure automatisée avec un échantillon provenant d'une chaîne de production par une bande convoyeuse.

Pour certaines mesures, notamment de texture ou de contraintes, il est nécessaire de faire varier la position de l'échantillon sous le faisceau (le faisceau est alors ponctuel). On utilise pour cela un goniomètre à trois cercles ou « berceau d'Euler » :

• balancement de l'échantillon (rocking) Ω (ou θ lorsque l'on est en géométrie Bragg-Brentano) ;
• inclinaison (tilt) χ ou ψ (la différence étant la référence 0) ;
• rotation dans le plan (spin) φ.

À ceci se rajoute la position 2θ du détecteur, on parle donc de « montage à quatre cercles ».

Le porte-échantillon peut aussi faire varier la position de l'échantillon selon les axes x, y et/ou z.

Détecteurs

Diffractomètre de monocristal

L'appareillage comporte un goniomètre pour manipuler le monocristal dans le faisceau de rayons X sous tous les angles (montage à quatre cercles). La rotation du cristal dans le diffractomètre a pour but de générer une onde issue des plans réticulaires en phase avec l'onde incidente à ce même plan réticulaire.

Cette technique est en général utilisée pour déterminer la structure cristalline.

La réception du signal

Elle se fait sur le CCD qui est une matrice de cellules qui captent l'information lumineuse sous forme de pixels et qui n'utilise pas de plaque photographique. Des photons isolés sont enregistrés électroniquement et répartis à l'aide d'un microprocesseur le long d'une série de pixels qui, assemblés en rangées, forment alors une image qui peut être numériquement travaillée par ordinateur.

Voir aussi

Bibliographie

• Parallel-beam coupling into channel-cut monochromators using curved graded multilayers, M. Schuster et H. Göbel, J Phys D 28 (1995) A270-275

Liens internes

• Diffractométrie de rayons X
• Théorie de la diffraction sur un cristal

Liens externes

• Tutorial on the conversion of powder X-ray diffraction films to synthetic digital diffractograms

Référence

• Portail de la physique