Critère d'irréductibilité de mackey

Critère d'irréductibilité de Mackey

George Mackey

En mathématiques, et plus précisément dans le cadre de la théorie des représentations d'un groupe, le critère d'irréductibilité de Mackey propose une condition nécessaire et suffisante pour qu'une représentation induite soit représentation irréductible.

Ce résultat^[1] est nommé en l'honneur du mathématicien George Whitelaw Mackey (1916-2006).

Sommaire

1 Énoncé
2 Contexte
- 2.1 Restriction d'une représentation induite à un sous-groupe
- 2.2 Réciprocité de Frobenius
3 Notes et références

Énoncé

Il est nécessaire de fixer le vocabulaire et les outils utilisés pour énoncer le critère.

Soient G un groupe fini et H un sous-groupe de G. K est un corps commutatif de caractéristique soit nulle soit première avec g l'ordre du groupe. Si K est de caractéristique finie alors il est algébrique. Dans tous les cas le polynôme X^g - 1 est scindé sur K.

Soit s un élément de G et H_s le sous-groupe intersection de H avec le conjugué de H par s. W est un espace vectoriel sur le corps K.

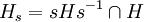
$H_s=sHs^{-1}\cap H$

Soit (W, θ) une représentation de H et (V, ρ) la représentation induite de G par (W, θ). θ^s désigne la représentation de H_s dans le groupe linéaire GL(W) défini par :

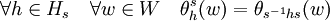
$\forall h \in H_s \quad \forall w \in W \quad \theta^s_h(w)=\theta_{s^{-1}hs}(w)$

On parle alors de représentation conjuguée de (W, θ).

Le critère de Mackey s'énonce de la manière suivante :

La représentation (V, ρ) est irréductible si et seulement si (W, θ) est irréductible et les différentes représentations θ^s restriction de θ à H_s sont disjointes quand s est un élément de G - H.

Il existe un corollaire, dans le cas où le groupe H est distingué :

La représentation induite de G par celle de H (W, θ) est irréductible si et seulement si (W, θ) est irréductible et n'est isomorphe à aucune représentation conjugué θ^s.

Remarque : Ce résultat se généralise dans le cas où le groupe est topologique localement compact et la représentation unitaire dans un espace de Hilbert.

Les démonstrations se trouvent dans la boîte déroulante ci-dessous.

Contexte

Restriction d'une représentation induite à un sous-groupe

Une question naturelle est celle de la nature d'une représentation induite sur la restriction de ρ à S. Pour cela, la définition des doubles classes modulo H et S est nécessaire :

Une double classe de G modulo H et S est un sous-ensemble E de G tel qu'il existe un élément s de G vérifiant E = SsH.

Il est aisé de vérifier que l'ensemble des doubles classes forment une partition de G. On dispose de la même définition que pour les classes à gauche ou à droite :

Un système de représentants C pour les doubles classes est sous-ensemble d'éléments c de G tel que ScH forment une partition de G si c parcourt C.

La restriction à S de la représentation induite (V, ρ) par (W, θ) est la somme directe des représentations induites de S par (W, θ^c) si c décrit C un ensemble de représentants des doubles classes de G modulo H et S.

Démonstrations

La restriction à S de la représentation induite (V, ρ) par (W, θ) est la somme directe des représentations induites de S par (W, θ^c) si c décrit C un ensemble de représentants des doubles classes de G modulo H et S.

Pour le démontrer, notons W_c le sous-espace de V somme des images de W par ρ(t) quand t décrit la double classe de c. On remarque que :

W_c est stable par S. En effet soit v un élément de W_c, alors il existe une famille (t_i) d'éléments de la double classe de c et une famille (w_i) d'éléments de W tel que :

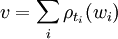
$v=\sum_{i}\rho_{t_i}(w_i)$

Si s un élément de S, alors st_i est élément de la double classe de c et :

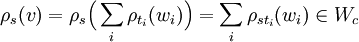
$\rho_s(v)=\rho_s\Big(\sum_{i}\rho_{t_i}(w_i)\Big)=\sum_{i}\rho_{st_i}(w_i)\in W_c$

La somme des W_c si c décrit C est égal V et la somme est directe. En effet, V est somme directe des images de W par ρ_h si h décrit un système de représentants R des classes à gauche de G modulo H car la représentation (V, ρ) est induite par celle de (W, θ) et les doubles classes forment une partition de R.
La représentation induite de S par (W, θ^c) est isomorphe à la représentation (W_c, ρ) restreinte à S. En effet, pour le vérifier, il suffit de montrer que la représentation (W, θ^c) de H_c est isomorphe à la représentation (ρ_cW, ρ) restreinte à H_c. Soient h' un élément de H_c et k l'élément de H tel que h= ckc^-1.

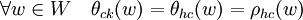
$\forall w \in W \quad \theta_{ck}(w)=\theta_{hc}(w)=\rho_{hc}(w)$

L'automorphisme ρ_c commute avec les deux représentations, ce qui termine la démonstration.

La représentation (V, ρ) est irréductible si et seulement si la restriction de θ^s à H_s sont disjointes quand s est un élément de G - H.

La démonstration est une application directe des résultats sur la restriction d'une application induite à un sous-groupe et de la formule de réciprocité de Frobenius. La représentation (V, ρ) est irréductible si et seulement si sa norme est égale à 1, c’est-à-dire <ρ , ρ> = 1. La formule de réciprocité de Frobenius s'exprime de la manière suivante :

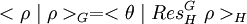
$<\rho \; |\; \rho>_G=<\theta \; |\; Res_H^G\; \rho>_H$

Or les résultats de l'analyse sur la restriction de ρ au sous-groupe H montre que cette restriction est isomorphe à la somme directe des représentations conjuguées de θ, si C est un système de représentants des doubles classes :

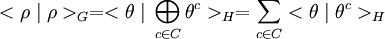
$<\rho \; |\; \rho>_G=<\theta \; |\; \bigoplus_{c \in C} \theta^c>_H=\sum_{c \in C}<\theta \; |\; \theta^c>_H$

En appliquant à nouveau la formule de Frobenius, cette fois-ci en sens inverse, on obtient :

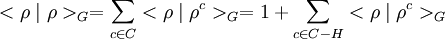
$<\rho \; |\; \rho>_G=\sum_{c \in C}<\rho \; |\; \rho^c>_G=1+\sum_{c \in C-H}<\rho \; |\; \rho^c>_G$

Ce qui termine la démonstration.

La représentation induite de G par celle de H (W, θ) est irréductible si et seulement si (W, θ) est irréductible et n'est isomorphe à aucune représentation conjuguée θ^s.

Il suffit de remarquer que H_s et H sont égaux.

Réciprocité de Frobenius

Article détaillé : Réciprocité de Frobenius.

Avec les notations du paragraphe précédent, la formule de réciprocité de Frobenius s'exprime par :

Si ψ et χ désignent les caractères respectifs de θ et ρ :

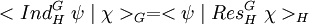
$<Ind_H^G \;\psi\; |\; \chi>_G=<\psi\; |\; Res_H^G\; \chi>_H$

Il est possible de généraliser la formule :

Soit f une fonction centrale de H et g une fonction centrale de G, alors l'égalité suivante est vérifiée :

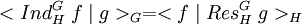
$<Ind_H^G \; f\; |\;g>_G=<f\; |\;Res_H^G \; g>_H$

Une autre manière d'exprimer cette propriété est la suivante :

L'application Ind_H^G est l'adjointe de Res_H^G.

Notes et références

Articles sur les Représentations d'un groupe d'ordre fini

Notes

↑ George W. Mackey Induced Representations of Locally Compact Groups IThe Annals of Mathematics, 2nd Ser., Vol. 55, No. 1 (Jan., 1952), pp. 101-139

Liens externes

(en) Georges Mackey Archive de la gazette de Harvard
(en) Induced Representations of Locally Compact Groups I le critère de Mackey par l'auteur dans le cas d'un groupe compact
(fr) Cours de représentation des groupes finis par M. Broué de l'université de Paris VII
(fr) Représentation linéaire des groupes finis, une introduction par D. Ferrand de l'université de Renne
(en) Finite group representations for the pure mathematician par Peter Web

Références

Jean-Pierre Serre, Représentations linéaires des groupes finis [détail des éditions]
(en) Marshall Hall, The theory of groups [détail des éditions]
Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
N. Bourbaki Algèbre, Chapitre VIII Paris, Hermann 1958

Portail des mathématiques

Ce document provient de « Crit%C3%A8re d%27irr%C3%A9ductibilit%C3%A9 de Mackey ».

Catégories : Théorie des représentations | Théorème d'algèbre

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Critère d'irréductibilité de mackey de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Critere d'irreductibilite de Mackey — Critère d irréductibilité de Mackey George Mackey En mathématiques, et plus précisément dans le cadre de la théorie des représentations d un groupe, le critère d irréductibilité de Mackey propose une condition nécessaire et suffisante pour qu une … Wikipédia en Français
Critère D'irréductibilité De Mackey — George Mackey En mathématiques, et plus précisément dans le cadre de la théorie des représentations d un groupe, le critère d irréductibilité de Mackey propose une condition nécessaire et suffisante pour qu une représentation induite soit… … Wikipédia en Français
Critère d'irréductibilité de Mackey — En mathématiques, et plus précisément dans le cadre de la théorie des représentations d un groupe, le critère d irréductibilité de Mackey propose une condition nécessaire et suffisante pour qu une représentation induite soit irréductible. Ce… … Wikipédia en Français
Critère — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un critère (du grec kriterion, de krinein, juger) est un principe auquel on se réfère, ou un moyen qu on utilise, pour établir un jugement. Cette notion… … Wikipédia en Français
Representation induite d'un groupe fini — Représentation induite d un groupe fini En mathématiques une représentation induite est une méthode de construction d une représentation d un groupe. Cet article traite le cas des groupes finis. Une représentation induite permet de construire à l … Wikipédia en Français
Représentation induite d'un groupe fini — En mathématiques une représentation induite est une représentation d un groupe canoniquement associée à une représentation de l un de ses sous groupes. L induction est adjointe à gauche de la restriction (en). Cette propriété intervient dans … Wikipédia en Français
Representation irreductible — Représentation irréductible En mathématiques, une représentation irréductible est un concept utilisé dans le cadre de la théorie des représentation d un groupe. Une représentation irréductible est une représentation qui n admet qu elle même et la … Wikipédia en Français
Représentation irréductible — En mathématiques, une représentation irréductible est un concept utilisé dans le cadre de la théorie des représentation d un groupe. C est une représentation qui n admet qu elle même et la représentation nulle comme sous représentation. Le… … Wikipédia en Français
Reciprocite de Frobenius — Réciprocité de Frobenius Ferdinand Georg Frobenius fondateur de la théorie des caractères En mathématiques, et plus précisément dans le cadre de la théorie des représentations d un groupe fini, la formule de réciprocité de Frobenius établit un… … Wikipédia en Français
Representations du groupe des quaternions — Représentations du groupe des quaternions En mathématiques les représentations du groupe des quaternions sont un exemple d application de la théorie des représentations d un groupe fini. Il illustre le théorème d Artin Wedderburn et met en… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Critère d'irréductibilité de mackey