Corps de nombre

Corps de nombre

Corps de nombres

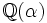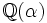En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l'élément primitif (ou théorème de l'extension monogène), tout corps de nombres peut s'écrire sous la forme \mathbb{Q}(\alpha) où α est un élément de K algébrique sur \mathbb{Q}(\alpha).

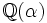Tout corps de nombres K peut ainsi être plongé comme un sous-corps de \mathbb{C}: il suffit d'envoyer α sur un nombre complexe ayant même polynôme minimal. Un tel élément existe, car tout polynôme a une racine dans \mathbb{C}; autrement dit \mathbb{C} est algébriquement clos. Réciproquement, le corps \mathbb{Q}(\alpha) est un corps de nombre pour tout nombre complexe α nombre algébrique sur \mathbb{Q}.

En outre, tous les éléments de K sont alors des nombres algébriques, dont le degré divise la dimension de K en tant qu'espace vectoriel sur \mathbb{Q}. Réciproquement les sous-corps de \mathbb{C} qui sont des corps de nombres sont ceux qui sont engendrés par un nombre fini de nombres algébriques.

En arithmétique les corps de nombres ont des propriétés très semblables aux corps de fonctions sur des courbes algébriques sur des corps finis.

Attention : Le corps des nombres algébrique n’est pas un corps de nombres algébriques. En effet le corps des nombres algébrique n’est pas une extension finie du corps \mathbb{Q}. Mais en revanche les éléments d’un corps de nombres algébriques sont nécessairement des nombres algébriques.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Corps de nombres ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Corps de nombre de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Corps De Nombres — En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la forme où α est… …   Wikipédia en Français

  • Corps De Nombres Algébriques — Corps de nombres En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la …   Wikipédia en Français

  • Corps de nombres algebriques — Corps de nombres En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la …   Wikipédia en Français

  • Corps de nombres algébriques — Corps de nombres En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la …   Wikipédia en Français

  • Corps des nombres algébriques — Corps de nombres En mathématiques, un corps de nombres est une extension finie et algébrique du corps des nombres rationnels. Par le théorème de l élément primitif (ou théorème de l extension monogène), tout corps de nombres peut s écrire sous la …   Wikipédia en Français

  • Nombre De Biot — Le nombre de Biot (Bi) est un nombre sans dimension utilisé dans les calculs de transfert thermique en phase transitoire. Il compare les résistances au transfert thermique à l intérieur et à la surface d un corps. Ce nombre porte le nom de Jean… …   Wikipédia en Français

  • Nombre de biot — Le nombre de Biot (Bi) est un nombre sans dimension utilisé dans les calculs de transfert thermique en phase transitoire. Il compare les résistances au transfert thermique à l intérieur et à la surface d un corps. Ce nombre porte le nom de Jean… …   Wikipédia en Français

  • Nombre Premier Régulier — En mathématiques, un nombre premier impair est dit régulier si une certaine propriété liée aux racines du polynôme xp 1 est vérifiée. Cette notion a été introduite par Ernst Kummer, pour une preuve du grand théorème de Fermat en 1847[1], dans un… …   Wikipédia en Français

  • Nombre premier irrégulier — Nombre premier régulier En mathématiques, un nombre premier impair est dit régulier si une certaine propriété liée aux racines du polynôme xp 1 est vérifiée. Cette notion a été introduite par Ernst Kummer, pour une preuve du grand théorème de… …   Wikipédia en Français

  • Nombre premier regulier — Nombre premier régulier En mathématiques, un nombre premier impair est dit régulier si une certaine propriété liée aux racines du polynôme xp 1 est vérifiée. Cette notion a été introduite par Ernst Kummer, pour une preuve du grand théorème de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”