Magma (mathématiques)
- Magma (mathématiques)
-
Magma (algèbre)
 Pour les articles homonymes
Pour les articles homonymes,
voir Magma.
Un magma (ou groupoïde) est une structure algébrique constituée d'un ensemble muni d'une loi de composition interne.
Aucun axiome n'est imposé sur cette loi de composition interne, souvent notée comme une multiplication. Le manque de richesse de cette structure algébrique fait qu'elle est rarement étudiée en tant que telle ; des magmas particuliers tel que les groupes, les monoïdes etc. sont bien plus souvent utiles.
Exemples de magmas
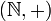 est un magma associatif, commutatif et unifère. De plus, tout élément y est régulier. Il s'agit donc d'un monoïde commutatif et régulier, donc un semigroupe commutatif.
est un magma associatif, commutatif et unifère. De plus, tout élément y est régulier. Il s'agit donc d'un monoïde commutatif et régulier, donc un semigroupe commutatif.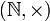 est également un monoïde commutatif, mais 0 n'étant pas régulier, ce n'est pas un semigroupe.
est également un monoïde commutatif, mais 0 n'étant pas régulier, ce n'est pas un semigroupe.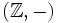 est un magma non-associatif et non-commutatif. Il n'est même pas unifère car, s'il admet un élément neutre à droite (0), il n'en admet pas à gauche. Par contre, ce magma est permutatif et régulier.
est un magma non-associatif et non-commutatif. Il n'est même pas unifère car, s'il admet un élément neutre à droite (0), il n'en admet pas à gauche. Par contre, ce magma est permutatif et régulier.- Murskii a montré en 1965 que le monoïde à trois éléments {0,1,2} muni de la loi interne *
| * |
0 |
1 |
2 |
| 0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
1 |
| 2 |
0 |
2 |
2 |
ne possède pas d'axiomatisation équationnelle (ou base équationnelle) finie.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Structure algébrique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Magma (mathématiques) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Magma (algebre) — Magma (algèbre) Pour les articles homonymes, voir Magma. Un magma (ou groupoïde) est une structure algébrique constituée d un ensemble muni d une loi de composition interne. Aucun axiome n est imposé sur cette loi de composition interne, souvent… … Wikipédia en Français
Magma (algèbre) — Pour les articles homonymes, voir Magma. En mathématiques, un magma (ou monade ou groupoïde de Ore[1]) est une structure algébrique constituée d un ensemble muni d une loi de composition interne. Ainsi si l on note E, un ensemble, et … Wikipédia en Français
Magma — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Magma », sur le Wiktionnaire (dictionnaire universel) Le terme Magma est d origine latine : il… … Wikipédia en Français
Ensembliste-Identitaire Et Mathématiques — Le philosophe du XXe siècle Cornelius Castoriadis a été tenté par une définition formelle de ses concepts d ontologies ensembliste identitaire et sociale historique, tentative apparemment abandonnée à la fin de sa vie. Sommaire 1 Partie… … Wikipédia en Français
Ensembliste-identitaire et mathematiques — Ensembliste identitaire et mathématiques Le philosophe du XXe siècle Cornelius Castoriadis a été tenté par une définition formelle de ses concepts d ontologies ensembliste identitaire et sociale historique, tentative apparemment abandonnée à … Wikipédia en Français
Ensembliste-identitaire et mathématiques — Le philosophe du XXe siècle Cornelius Castoriadis a été tenté par une définition formelle de ses concepts d ontologies ensembliste identitaire et sociale historique, tentative apparemment abandonnée à la fin de sa vie. Sommaire 1 Partie… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Groupe (mathématiques) — Pour les articles homonymes, voir Groupe. Les manipulations possibles du cube de Rubik forment un groupe. En mathématiques, un groupe est un ensemble … Wikipédia en Français
Algèbre universelle — Pour les articles homonymes, voir Algèbre (homonymie). L algèbre universelle est la branche de l algèbre qui a pour but de traiter de manière générale et simultanée les différentes structures algébriques : groupes, monoïdes, anneaux, espaces … Wikipédia en Français
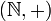 est un magma associatif, commutatif et unifère. De plus, tout élément y est régulier. Il s'agit donc d'un monoïde commutatif et régulier, donc un semigroupe commutatif.
est un magma associatif, commutatif et unifère. De plus, tout élément y est régulier. Il s'agit donc d'un monoïde commutatif et régulier, donc un semigroupe commutatif.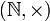 est également un monoïde commutatif, mais 0 n'étant pas régulier, ce n'est pas un semigroupe.
est également un monoïde commutatif, mais 0 n'étant pas régulier, ce n'est pas un semigroupe.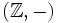 est un magma non-associatif et non-commutatif. Il n'est même pas unifère car, s'il admet un élément neutre à droite (0), il n'en admet pas à gauche. Par contre, ce magma est permutatif et régulier.
est un magma non-associatif et non-commutatif. Il n'est même pas unifère car, s'il admet un élément neutre à droite (0), il n'en admet pas à gauche. Par contre, ce magma est permutatif et régulier.