- Propriete universelle
-
Propriété universelle
En mathématiques, une propriété universelle est la propriété des objets qui sont la solution d'un problème universel posé par un foncteur.
Propriété universelle des modules quotients
Soient
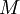 et
et 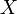 deux A-modules, soit
deux A-modules, soit 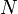 un sous-module de
un sous-module de 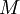 , soit
, soit 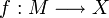 une application A-linéaire.
une application A-linéaire.Alors il existe une unique application
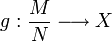 A-linaire telle que
A-linaire telle que 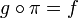 ssi
ssi 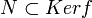 , i.e. ssi
, i.e. ssi 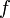 est constante sur les classes, avec
est constante sur les classes, avec 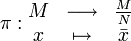 la surjection canonique.
la surjection canonique.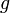 est l'application déduite de
est l'application déduite de 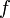 par passage au quotient ; et on a le diagramme :
par passage au quotient ; et on a le diagramme :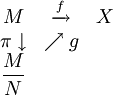 Démonstration
DémonstrationPar analyse-synthèse :
- Supposons qu'une telle application
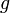 existe.
existe.
Soit
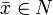 : on a
: on a 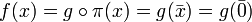 car
car 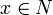 et
et 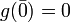 car
car 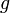 est A-linéaire.
est A-linéaire.On a bien
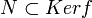 , donc
, donc 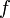 est bien constante sur les classes.
est bien constante sur les classes.- Supposons
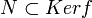 :
:
Par analyse-synthèse :
Posons
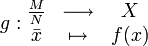 On a
On a 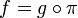 ; montrer que
; montrer que 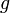 est bien défini :
est bien défini :soient
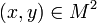 tels que
tels que 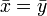
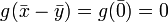 et
et 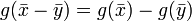 donc
donc 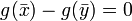 donc
donc 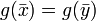 donc
donc 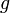 bien définie et unique.
bien définie et unique.soit
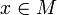 ,
, 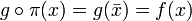 donc
donc 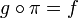 , ce qui assure l'existence de
, ce qui assure l'existence de 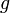 .
.Propriété universelle de la somme directe externe
Soit A un anneau ; soit
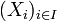 une famille de A-modules, Y un A-module ; soit
une famille de A-modules, Y un A-module ; soit 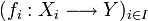 une famille d'applications linéaires.
une famille d'applications linéaires.Alors il existe une unique application
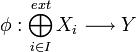 A-linéaire telle que :
A-linéaire telle que : 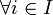 ,
, 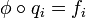 avec
avec 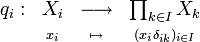 l'injection canonique.Démonstration
l'injection canonique.DémonstrationPar analyse synthèse :
- Supposons qu'un tel
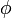 existe. Soit
existe. Soit 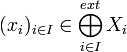 ; on a :
; on a :
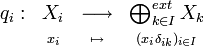 avec
avec 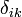 symbole de Kronecker ; on a :
symbole de Kronecker ; on a : 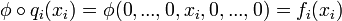 et, pour
et, pour 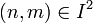 ,
, 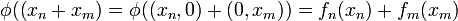 par A-linéarité, donc
par A-linéarité, donc 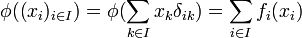 ce qui assure l'unicité de φ
ce qui assure l'unicité de φ- Posons donc
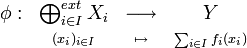 ; les
; les 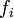 étant linéaires,
étant linéaires, 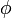 est linéaire.
est linéaire.
Soit
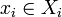 , on a :
, on a : 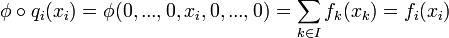 ; ainsi nous avons bien
; ainsi nous avons bien 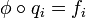 , donc
, donc 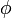 existe bien.
existe bien.Propriété universelle des modules libres
Soit M un module libre de base
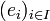 ; soit Y un autre module, soit
; soit Y un autre module, soit 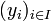 une famille de vecteurs de Y.
une famille de vecteurs de Y.Alors il existe une unique application linéaire
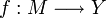 telle que
telle que 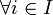 ,
, 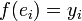 Démonstrations
DémonstrationsPar analyse synthèse :
- Supposons qu'une telle application f existe. Soit
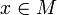 , il existe
, il existe 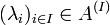 telle que
telle que 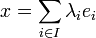 ; donc :
; donc :
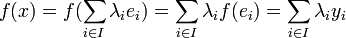
- Posons donc
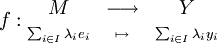
f est linéaire, ce qui se démontre aisément ; soit
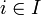 ,
, 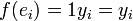
f existe et est unique.
Propriété universelle du produit
Soit
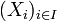 une famille de A-modules ; soit
une famille de A-modules ; soit 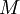 un A-module ; soit
un A-module ; soit 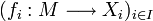 une famille d'applications linéaires.
une famille d'applications linéaires.Alors il existe une unique application linéaire
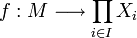 telle que
telle que 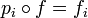
avec
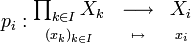 l'i-ème projection canonique.
l'i-ème projection canonique.On a donc le diagramme suivant :
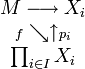 Démonstration
DémonstrationPar analyse-synthèse :
Posons
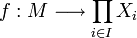
Soit
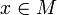 :
: 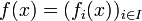 , et on a bien :
, et on a bien : 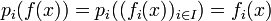
Soit
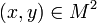 et
et 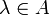 :
: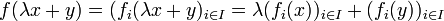 car les
car les 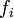 sont linéaires.
sont linéaires.Donc
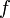 est linéaire, et elle existe.
est linéaire, et elle existe.Propriété universelle des anneaux fractionnaires
Soit
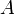 un anneau commutatif ; soit
un anneau commutatif ; soit 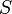 une partie multiplicative de
une partie multiplicative de 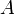 ; soit
; soit 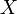 un anneau commutatif, et
un anneau commutatif, et 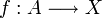 un morphisme d'anneau tel que :
un morphisme d'anneau tel que : 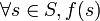 inversible. On définit la relation d'équivalence
inversible. On définit la relation d'équivalence 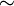 sur
sur 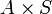 par
par 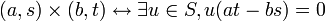 .
.Alors il existe un unique morphisme
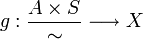 tel que
tel que 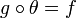 , avec
, avec 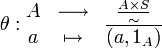 On a le diagramme suivant :
On a le diagramme suivant :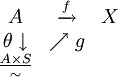 Démonstration
DémonstrationPar analyse-synthèse :
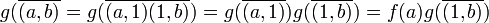 .
.
Or
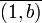 inverse de
inverse de 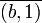 : en effet
: en effet 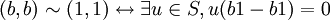 .
.Donc
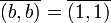 ,
, 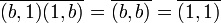 ; donc
; donc 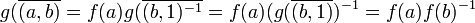
- Posons
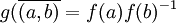
Montrons que
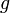 est constant sur les classes. Soient
est constant sur les classes. Soient 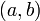 et
et 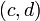 tels que
tels que 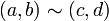 : Montrons que
: Montrons que 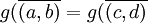 : cela revient à montrer que
: cela revient à montrer que 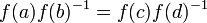 , i.e.
, i.e. 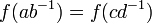 , i.e.
, i.e. 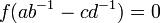 car
car 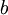 et
et 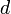 sont dans
sont dans 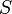 On a :
On a : 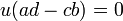
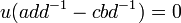
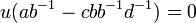
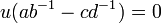
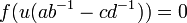
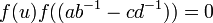 , or
, or 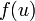 est inversible, donc non null. Donc
est inversible, donc non null. Donc 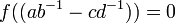 , donc
, donc 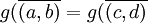 ,
, 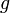 est bien défini.
est bien défini.Propriété universelle des corps fractionnaires
Cette propriété universelle est un cas particulier de la propriété universelle des anneaux fractionnaires.
Soit
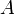 un anneau commutatif intègre; soit
un anneau commutatif intègre; soit 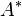 l'ensemble des éléments non nulls de
l'ensemble des éléments non nulls de 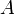 ; soit
; soit 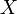 un anneau commutatif, et
un anneau commutatif, et 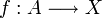 un morphisme d'anneau. On définit la relation d'équivalence
un morphisme d'anneau. On définit la relation d'équivalence 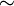 sur
sur 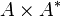 par
par 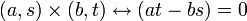 .
.Alors il existe un unique morphisme
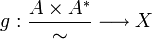 tel que
tel que 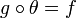 .
.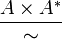 est un corps.
est un corps.Propriété universelle des algèbres
Soient
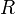 un corps,
un corps, 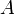 une R-algèbre,
une R-algèbre, 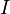 un idéal bilatère de
un idéal bilatère de 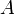 ,
, 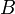 une R-algèbre. Soit
une R-algèbre. Soit 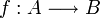 un morphisme d'algèbre tel que
un morphisme d'algèbre tel que 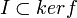 .
.Alors il existe un unique morphisme d'algèbre
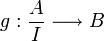 tel que
tel que 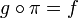 avec
avec 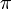 la surjection canonique.
la surjection canonique.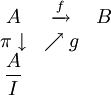 Démonstration
Démonstration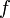 est un morphisme de R-module. La propriété universelle des modules quotients assure qu'il existe
est un morphisme de R-module. La propriété universelle des modules quotients assure qu'il existe 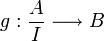 R-linéaire tel que
R-linéaire tel que 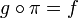 . Il suffit donc de montrer que
. Il suffit donc de montrer que 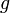 est un morphisme d'algèbre :
est un morphisme d'algèbre :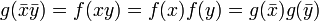
Propriété universelle des groupes quotients
Cette propriété est similaire à celle des modules quotients.
Soient
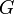 et
et 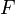 deux groupes, soit
deux groupes, soit 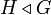 Soit
Soit 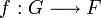 un morphisme de groupes tel que
un morphisme de groupes tel que 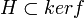 .
.Alors il existe un unique morphisme de groupe
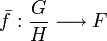 tel que
tel que 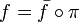 avec
avec 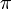 la surjection cannonique.
la surjection cannonique.La démonstration de cette propriété est semblable à celle de la propriété universelle des modules quotients, sauf qu'on suppose dans les prémisses que
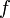 est constante sur les classes. Par ailleurs, on introduit la normalité de
est constante sur les classes. Par ailleurs, on introduit la normalité de 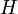 dans
dans 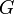 pour ne pas avoir à énoncer la propriété pour le groupe quotient à gauche et pour le groupe quotient à droite.
pour ne pas avoir à énoncer la propriété pour le groupe quotient à gauche et pour le groupe quotient à droite.Voir aussi
- Portail des mathématiques
Catégorie : Logique - Supposons qu'une telle application
Wikimedia Foundation. 2010.
