Axiome de séparation (topologie)

Axiome de séparation (topologie)
Page d'aide sur l'homonymie Ne pas confondre avec le schéma d'axiomes de séparation de la théorie des ensembles.

En topologie, un axiome de séparation est une propriété satisfaite par certains espaces topologiques, similaire à la propriété de séparation de Hausdorff (dite aussi T2), et concernant la séparation de points ou de fermés, en termes soit de voisinages, soit de fonctions continues réelles.

Divers axiomes de séparation peuvent être ordonnés par implication, notamment ceux de la série des axiomes codés par la lettre « T »[1] et un indice numérique, ces axiomes étant en général[2] d'autant plus restrictifs que les indices sont élevés et les topologies correspondantes plus fines.

Attention : dans la littérature, le vocabulaire est parfois très volatil et certaines de ces définitions peuvent être interchangées.

Sommaire

Liste d'axiomes

La séparation T0 (espace de Kolmogorov)

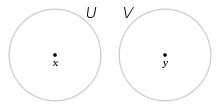
Dans un espace topologique X, deux points x et y sont dits indiscernables s'ils appartiennent exactement aux mêmes ouverts, ou encore s'ils ont exactement les mêmes voisinages. C'est une relation d'équivalence. On dira que X est un espace T0 lorsque les classes d'équivalence sont toutes réduites à des singletons. Autrement dit, pour deux points distincts quelconques, l'un des deux points admet un voisinage qui ne contient pas l'autre point. Ou encore, l'un des deux points n'est pas adhérent à l'autre.

Un espace vérifiant cette propriété est parfois appelé espace de Kolmogorov. Tout espace de Kolmogorov X est homéomorphe à un sous-espace du produit [0,1]I, où I est l'ensemble des applications continues de X dans [0,1], chaque ensemble [0,1] étant muni de la topologie droite[3].

Le quotient d'un espace topologique quelconque X par la relation d'équivalence précédente, appelé quotient de Kolmogorov, est toujours un espace de Kolmogorov.

La séparation T1 (espace accessible, ou de Frechet)

Un espace topologique X est un espace T1 si les singletons de X sont fermés. Ceci équivaut à : pour tout point x, l'intersection des voisinages de x est réduite au singleton {x}. Ou encore, pour deux points distincts quelconques, chacun des deux points admet un voisinage qui ne contient pas l'autre point. Ou encore, aucun des deux points n'est adhérent à l'autre.

Un espace est T1 si et seulement s'il est à la fois T0 et R0.

L'espace E = {a,b} dont les ouverts sont \varnothing, {a}, E est T0 mais pas T1. De même pour l'ensemble des réels muni de la topologie droite.

Hausdorff space.svg

La séparation T2 (espace de Hausdorff)

C'est la propriété classique. Un espace topologique est dit T2, ou de Hausdorff, ou espace séparé, si pour tout couple (x,y) d'éléments distincts de X, il existe deux ouverts disjoints dont l'un contient x et l'autre contient y. Ceci équivaut à : pour tout point x, l'intersection des voisinages fermés de x est réduite au singleton {x}.

La séparation T2 entraîne la séparation T1. La réciproque est fausse : la topologie cofinie, et la topologie de Zariski sur une variété algébrique, sont T1 mais en général non séparées.

La séparation T2 1/2 (espace complètement de Hausdorff)

Un espace topologique est un espace T2 1/2 lorsque deux points distincts admettent des voisinages dont les adhérences sont disjointes. Ou encore, deux points distincts admettent des voisinages fermés disjoints.

Un espace T2 qui n'est pas T2 1/2

Tout espace T2 1/2 est séparé mais la réciproque est fausse, comme le montre l'exemple suivant. On considère l'ensemble E du plan constitué de l'intérieur du disque de centre O de rayon 1 et des deux points (1,0) et (-1,0). Une base de voisinages d'un point intérieur au disque est formée des disques centrés en ce point. Une base de voisinages du point (1,0) est constituée des réunions de ce point et d'une bande semi-circulaire (ouverte au sens usuel) adjacente à ce point et limitée par des segments [(0,1), (0,1-h)] et [(0,-1), (0,-1+h)]. De même pour (-1,0). Dans le dessin ci-dessous, on a représenté en couleur un voisinage d'un point intérieur au disque, et un voisinage de chacun des points (1,0) et (-1,0). Si ces deux derniers voisinages sont ouverts, ils sont disjoints, mais leurs adhérences s'intersectent selon une partie des segments communs qui les limitent. L'espace E est donc séparé mais pas T2 1/2.

La séparation T2 3/4 (espace d'Urysohn)

Un espace topologique X est appelé espace d'Urysohn lorsque pour tous points distincts x et y de X, il existe une fonction continue f de X dans le segment [0,1] telle que f(x)=0 et f(y)=1. Un espace d'Urysohn est T2 1/2.

Un espace est d'Urysohn si et seulement si l'application canonique vers son compactifié de Stone-Čech est injective.

Regular space.svg

Séparation T3 et espaces réguliers

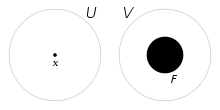
Un espace topologique X vérifie T3 lorsque pour tout point x de X et pour tout fermé F de X ne contenant pas x, il existe deux ouverts disjoints dont l'un contient x et l'autre contient F.

On remarquera qu'un espace peut vérifier T3 sans être séparé : la topologie grossière vérifie T3. Par contre si X vérifie T3 et T0 alors il est séparé.

Un espace séparé vérifiant T3 est appelé espace régulier.

Un tel espace vérifie T2 1/2, mais pas toujours T2 3/4.

Séparation T3 1/2 et espaces complètement réguliers (ou de Tychonov)

Un espace topologique X vérifie T3 1/2 si pour tout point x de X et pour tout fermé F de X ne contenant pas x, il existe une fonction continue de X dans le segment [0,1] valant 0 en x et 1 sur F. Ceci équivaut à : X est uniformisable[4].

On remarquera qu'un espace peut être uniformisable sans être séparé : la topologie grossière vérifie T3 1/2. Par contre si X vérifie T3 1/2 et T0 alors il est séparé.

Un espace séparé vérifiant T3 1/2 est qualifié de complètement régulier (on dit aussi espace de Tychonov).

Tout espace X complètement régulier est homéomorphe à un sous-espace du produit [0,1]I, où I est l'ensemble des applications continues de X dans [0,1], et où chaque ensemble [0,1] est muni de la topologie usuelle[3]. Comme [0,1]I est compact, X est homéomorphe à un sous-espace d'un espace compact. Son adhérence dans [0,1]I est le compactifié de Stone-Čech de X. Réciproquement, un sous-espace d'un espace compact est complètement régulier.

Un espace complètement régulier est donc non seulement régulier mais aussi d'Urysohn.

Normal space.svg

Séparation T4 et espaces normaux

Un espace topologique X vérifie T4 lorsque pour tout couple de fermés disjoints E et F, il existe un couple d'ouverts disjoints dont l'un contient E et l'autre contient F.

Cet axiome n'est pas préservé par sous-espaces ni par produits. Cependant, tout sous-espace fermé d'un espace T4 est T4.

Démonstration

Soit X un espace T4, Y un sous-espace fermé. Soit F et G deux fermés de Y disjoints. Y étant fermé, ce sont aussi deux fermés de X. Donc ils peuvent être séparés dans X par deux ouverts disjoints U et V, U contenant F et V contenant G. Mais alors U \cap Y et V \cap Y sont des ouverts disjoints de Y séparant F et G dans Y.

Cet axiome n'implique aucun des précédents. En particulier, un espace peut vérifier T4 sans être séparé : la topologie grossière vérifie T4. Par contre si un espace vérifie T4 et T1 alors il est séparé.

Un espace séparé vérifiant T4 est qualifié de normal.

Si X vérifie T4, pour tout couple de fermés disjoints E et F, il existe une fonction continue de X dans le segment [0,1] valant 0 sur E et 1 sur F. Cette propriété remarquable s'appelle le lemme d'Urysohn. Plus généralement, le théorème de prolongement de Tietze assure que toute fonction continue d'un fermé de X dans R s'étend continûment à X.

En particulier, tout espace normal est complètement régulier.

Tout espace compact est normal.

Séparation T5 et espaces complètement normaux

Un espace topologique X vérifie T5 si pour toutes parties A et B de X telles que A\cap\overline{B}=\varnothing et B\cap\overline{A}=\varnothing, il existe deux ouverts disjoints dont l'un contient A et l'autre contient B.

Ceci équivaut à : tout sous-espace de X vérifie T4.

Démonstration
  • Premièrement l'implication ; soient X vérifiant T5 et Y un sous-espace de X. Alors Y vérifie T5 (donc T4). En effet, pour toutes parties A et B de Y, l'adhérence de B dans le sous-espace Y (muni de sa topologie induite) est égale à \overline{B}\cap Y, donc est disjointe de A si A\cap\overline{B}=\varnothing (et de même en échangeant les rôles de A et B). Par hypothèse sur X, deux telles parties A et B sont donc séparées par deux ouverts de X disjoints. Les traces sur Y de ces deux ouverts sont alors deux ouverts de Y disjoints qui séparent A et B.
  • Ensuite la réciproque ; soit X un espace topologique dont tous les sous-espaces vérifient T4. Soient A et B deux parties de X telles que A\cap\overline{B}=\varnothing et B\cap\overline{A}=\varnothing. On pose Y=X\setminus (\overline{A}\cap\overline{B}). Il vient A \subset \overline{A}\cap Y et B \subset \overline{B}\cap Y. Or \overline{A}\cap Y et \overline{B}\cap Y sont disjoints et sont deux fermés du sous-espace Y (muni de sa topologie induite). Comme Y vérifie T4, il existe deux ouverts OA∩Y et OB∩Y qui séparent ces fermés, et a fortiori séparent A et B. Comme Y est lui-même un ouvert de X, les ensembles OA∩Y et OA∩Y sont des ouverts de X ; il vient que X vérifie T5.

Un espace séparé vérifiant T5 est qualifié de complètement normal.

Un espace est donc complètement normal si et seulement si tous ses sous-espaces sont normaux.

La séparation T5 1/2 (espace parfaitement normal)

Un espace séparé X est dit parfaitement normal si tout fermé de X est le lieu d'annulation d'une application continue f de X dans R.

Tout espace métrisable est parfaitement normal (prendre pour f la fonction distance au fermé).

Tout sous-espace d'un espace parfaitement normal est encore parfaitement normal.

Un espace parfaitement normal est normal (et par suite complètement normal, d'après la stabilité précédente pour les sous-espaces). Mieux : pour tous fermés disjoints E et F d'un tel espace X, e et f étant des fonctions continues qui s'annulent exactement sur ces fermés, la fonction \frac{|e|}{|e|+|f|}:X\to[0,1] est continue, et vaut 0 exactement sur E et 1 exactement sur F.

La définition originelle (due à Čech et équivalente)[5] est : un espace est parfaitement normal s'il est normal et chacun de ses fermés est un Gδ, c'est-à-dire une intersection dénombrable d'ouverts (en l'occurrence \bigcap_{n=1}^{+\infty}f^{-1}\left(\,\left]-1/n,1/n\right[\,\right)).

Notes et références

  1. ↑ Cette lettre, initiale du mot allemand Trennungsaxiom (« axiome de séparation »), a été introduite par Pavel Aleksandrov et Heinz Hopf dans leur traité Topologie de 1935 (p. 58 et suivantes), où ils présentaient une liste de tels axiomes (cf (en)Earliest Known Uses of Some of the Words of Mathematics, par Jeff Miller).
  2. ↑ Plus précisément, on a ici les implications suivantes (et celles qui s'en déduisent immédiatement) :
    T_5\Rightarrow T_4,\quad T_4\land T_1\Rightarrow T_{3\; 1/2},\quad T_{3\; 1/2}\Rightarrow T_3,
    T_{3\; 1/2}\land T_0\Rightarrow T_{2\; 3/4},\quad T_3\land T_0\Rightarrow T_{2\; 1/2},
    T_{2\; 3/4}\Rightarrow T_{2\; 1/2}\Rightarrow T_2\Rightarrow T_1\Rightarrow T_0.
  3. ↑ a et b François Guénard et Gilbert Lelièvre, Compléments d'analyse, Vol. 1 : Topologie, première partie, ENS Fontenay éd., 1985 [lire en ligne], p. 28 
  4. ↑ Guénard et Lelièvre 1985, p. 35
  5. ↑ N. Vedenissoff, « Généralisation de quelques théorèmes sur la dimension », dans Compositio Mathematica, vol. 7, 1940, p. 194-200 [texte intégral] 

Bibliographie

Article connexe

Histoire des axiomes de séparation (en)


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Axiome de séparation (topologie) de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Axiome de séparation — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En mathématiques, l expression axiome de séparation est utilisée de façon indépendante dans deux domaines : en topologie, un axiome de séparation est …   Wikipédia en Français

  • Séparation (mathématiques) — Pour les articles homonymes, voir Séparation. En topologie et en géométrie, la séparation est une propriété caractérisant la possibilité de séparer de manière convenable deux parties disjointes données d un espace topologique. La manière de… …   Wikipédia en Français

  • Topologie de l'ordre — En mathématiques, la topologie de l ordre est une topologie naturelle définie sur tout ensemble ordonné (E,≤), et qui dépend de la relation d ordre ≤. Lorsque l on définit la topologie usuelle de la droite numérique , deux approches équivalentes… …   Wikipédia en Français

  • Glossaire de topologie — Ceci est un glossaire de quelques termes utilisés en topologie. Ce glossaire est divisé en deux parties. La première traite des concepts généraux, et la seconde liste différents types d espaces topologiques. Dans ce glossaire, tous les espaces… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Espace normal — Un espace topologique séparable X est dit normal lorsque, pour tout couple de fermés disjoints E et F de X, il existe un couple d ouverts disjoints U et V tels que U contienne E et V, F. En mathématiques, un espace normal est un cas particulier d …   Wikipédia en Français

  • Lemme d'Urysohn — Le mathématicien Pavel Urysohn donne son nom au lemme de l article. Le lemme d Urysohn est un résultat de topologie, qui établit que pour deux fermés disjoints A et B d un espace normal X (ou plus généralement d un espace T4), il existe une… …   Wikipédia en Français

  • Espace R0 — En topologie, un espace symétrique (ou espace R0) est un cas particulier d espace topologique. Il s agit d un exemple d axiome de séparation. Sommaire 1 Définition 2 Propriétés 3 Exemples …   Wikipédia en Français

  • Glossaire Topologique — Cette page est une annexe de : Topologie Glossaire topologique Annexe de : Topologie Ceci est un glossaire de quelques termes utilisés en topologie. Ce glossaire est divisé en deux parties. La première …   Wikipédia en Français

  • Glossaire topologique — Cette page est une annexe de : Topologie Glossaire topologique Annexe de : Topologie Ceci est un glossaire de quelques termes utilisés en topologie. Ce glossaire est divisé en deux parties. La première …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”