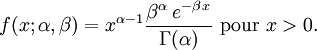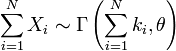Loi Gamma

Distribution Gamma

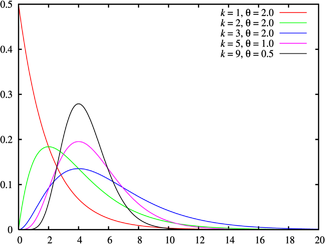
**Loi Gamma**
Densité de probabilité / Fonction de masse
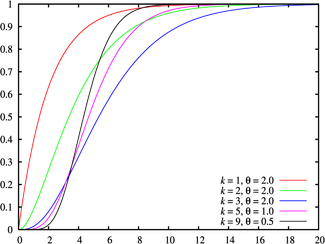
Fonction de répartition >
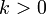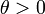Paramètres	$k > 0\,$ réel $\theta > 0\,$ réel
Support	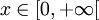$x \in [0,+ \infty[$
Densité de probabilité (fonction de masse)	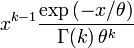$x^{k-1} \frac{\exp\left(-x/\theta\right)}{\Gamma(k)\,\theta^k}$
Fonction de répartition	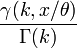$\frac{\gamma(k, x/\theta)}{\Gamma(k)}$
Espérance	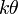$k \theta\,$
Médiane (centre)	pas d'expression formelle
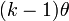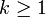
Mode	$(k-1) \theta\,$ pour $k \geq 1\,$
Variance	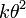$k \theta^2\,$
Asymétrie (statistique)	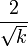$\frac{2}{\sqrt{k}}$
Kurtosis (non-normalisé)	$\frac{6}{k}$
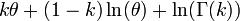
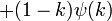
Entropie	$k\theta+(1-k)\ln(\theta)+\ln(\Gamma(k))\,$ $+(1-k)\psi(k)\,$
Fonction génératrice des moments	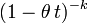$(1 - \theta\,t)^{-k}$ pour $t < 1 / θ$
Fonction caractéristique	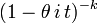$(1 - \theta\,i\,t)^{-k}$

En théorie des probabilités et en statistiques, une distribution Gamma, ou loi Gamma, est un type de loi de probabilité de variables aléatoires réelles positives. La famille des distributions Gamma inclut entre autres les lois exponentielles, les lois de sommes de variables aléatoires indépendantes suivant une même loi exponentielle, ainsi que la loi du χ². Elle permet donc de modéliser une grande variété de phénomènes pour des grandeurs positives.

Une variable aléatoire X suit une loi Gamma de paramètres $k$ et $θ$ (strictement positifs), ce que l'on note aussi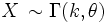 $X \, \sim \Gamma(k, \theta)$ , si sa fonction de densité de probabilité peut se mettre sous la forme :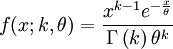

$f(x;k,\theta) = \frac{{x^{k - 1} e^{ - \frac{x}{\theta }} }}{{\Gamma \left( k \right) \theta ^k }}$

Alternativement, la distribution gamma peut être paramétrée à l'aide d'un paramètre de forme $α = k$ et d'un paramètre d'échelle $β = 1 / θ$ :

$f(x;\alpha,\beta) = x^{\alpha-1} \frac{\beta^{\alpha} \, e^{-\beta\,x} }{\Gamma(\alpha)} \ \mathrm{pour}\ x > 0 \,\!.$

Les deux paramétrages sont aussi répandus, selon la configuration.

Sommaire

1 Propriétés
- 1.1 Somme
- 1.2 Scaling
2 Lien avec les autres distributions
- 2.1 Contraintes sur les paramètres
- 2.2 Autres manipulations
3 Voir aussi

Propriétés

Somme

Si chaque X_i suit la loi Γ(k_i, θ) pour i = 1, 2, ..., N, et si les variables aléatoires X_i sont indépendantes, alors :

$\sum_{i=1}^N X_i \sim \Gamma \left( \sum_{i=1}^N k_i, \theta \right) \,\!$

Scaling

Pour tout t > 0, la variable tX est distribuée selon Γ(k, (1/t)θ), du moment que θ est un paramètre d'échelle.

Lien avec les autres distributions

Contraintes sur les paramètres

Si 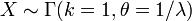$X \sim {\Gamma}(k=1, \theta=1/\lambda)\,$ , alors X a une distribution exponentielle de paramètre λ.
Si 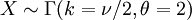$X \sim {\Gamma}(k=\nu/2, \theta=2)\,$ , alors X est identique à une variable χ²(ν), la distribution de la loi du χ² avec ν degré de liberté.
Si $k$ est un entier, la loi gamma est une distribution d'Erlang;
Si 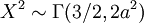$X^2 \sim {\Gamma}(3/2, 2a^2)\,$ , alors X a une distribution de Maxwell-Boltzmann avec comme paramètre a.

Autres manipulations

Si X a une distribution Γ(k, θ), alors 1/X a une distribution loi gamma inverse, de paramètres k et θ^-1.
Si X et Y sont distribuées indépendamment selon des lois Γ(α, θ) et Γ(β, θ) respectivement, alors X / (X + Y) a une distribution beta de paramètres α et β.
SiX_i sont distribuées selon des lois Γ(α_i,θ) respectivement, alors le vecteur (X₁ / S, ..., X_n / S), où S = X₁ + ... + X_n, suit une distribution de Dirichlet de paramètres α₁, ..., α_n.
Pour k grand, la distribution gamma converge vers une loi normale, de moyenne $μ = (k - 1)θ$ et de variance $σ 2 = (k - 1)θ 2$ .

Voir aussi

Ce document provient de « Distribution Gamma ».

Catégorie : Loi de probabilité

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi Gamma de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Loi gamma — ● Loi gamma loi de probabilité d une variable aléatoire continue X prenant ses valeurs dans [0,+∞] et ayant pour densité de probabilité , Γ(x) étant la fonction gamma et m un paramètre positif. (Pour m = 1, on a la loi exponentielle avec λ = 1.) … Encyclopédie Universelle
Loi gamma — Distribution Gamma Loi Gamma Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
gamma — [ ga(m)ma ] n. m. • transcrit 1824; mot gr. 1 ♦ Troisième lettre de l alphabet grec (Γ, γ), correspondant au G [ g ] . 2 ♦ POINT GAMMA.Astron. Intersection de l écliptique avec le plan de l équateur. ⇒ vernal. Arg. scol. Fête de l École… … Encyclopédie Universelle
Loi log-normale — Densité de probabilité / Fonction de masse μ=0 Fonction de répartition μ=0 … Wikipédia en Français
Loi logistique — Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi uniforme discrète — Densité de probabilité / Fonction de masse n=5 où n = b − a + 1 Fonction de répartition … Wikipédia en Français
Loi inverse-gamma — Inverse gamma Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi binomiale négative — Binomiale négative Densité de probabilité / Fonction de masse La ligne rouge représente la moyenne et la ligne verte a pour longueur approximativement 2σ. Paramètres (réel) … Wikipédia en Français
Loi de Student — Pour le test statistique, voir Test t. Loi de Student Densité de probabilité / Fonction de masse Fonction de répartition … Wikipédia en Français
Loi du χ² — Pour les méthodes expérimentales, voir [[test du χ2]] et méthode des moindres carrés. Loi du χ2 Densité de probabilité / Fonction de masse … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Loi Gamma

Distribution Gamma

Sommaire