Algorithme De Viterbi

L'algorithme de Viterbi, d'Andrew Viterbi, permet de corriger les erreurs survenues lors d'une transmission à travers un canal bruité (dans une certaine mesure).

Son utilisation s'appuie sur la connaissance du canal bruité (la probabilité qu'une information ait été modifiée en une autre) et permet de simplifier radicalement la complexité de la recherche du plus probable message d'origine (d'exponentielle, cette complexité devient linéaire).

Cet algorithme a pour but de trouver la séquence d'états la plus probable ayant produit la séquence mesurée.

Sommaire 1 Principe 2 Applications 3 Exemple 4 Références 5 Liens externes

Principe

Soit un message m diffusé à travers un canal bruité connu (par exemple, qui supprime tous les accents d'un texte) et le message o observé en sortie du canal.

Pour retrouver le message d'origine, on cherche, à partir de o le message le plus probable. La méthode brute consiste à tester, pour chaque lettre de o la lettre la plus probable dans m en émettant l'hypothèse que le canal bruité n'a pas ajouté ni supprimé d'information.

On obtient un arbre de taille importante, si n est la taille du message et a le nombre de modifications possibles pour chaque unité (chaque lettre par exemple), la complexité du traitement est de aⁿ (ce qui rend le problème incalculable pour de grandes quantités de données).

L'algorithme de Viterbi propose de simplifier l'arbre au fur et à mesure de sa construction. En effet, lors de son déroulement on se retrouve rapidement avec des branches proposant les mêmes substitutions, mais avec des probabilités différentes : il n'est pas nécessaire de dérouler celles de plus faible probabilité puisqu'elles ne peuvent plus être candidates pour décrire le message le plus probable. Ce principe simple est connu sous le nom de programmation dynamique.

De manière plus générale, l'algorithme de Viterbi est utilisé dans les cas ou le processus sous-jacent est modélisable comme une chaîne de Markov discrète à états finis. Le problème est alors, étant donné une séquence d'observation z, de trouver la séquence d'états x pour laquelle la probabilité a posteriori P(x | z) est maximale. L'algorithme de Viterbi donne la solution de ce problème d'estimation par maximum a posteriori.

Applications

L'application la plus courante est probablement la restauration de transmissions numériques, détériorées à travers un canal non fiable (transmission hertzienne par exemple) en s'appuyant sur la distance de Hamming afin de faire ressortir la plus faible métrique entre les différentes valeurs probables. En général, cette méthode s'applique à de nombreux problèmes basés sur des évaluations statistiques de la pertinence des résultats (abondamment utilisé en traitement automatique des langues par exemple, cf exemple suivant).

Une des applications phares de l'algorithme est aussi l'estimation de la séquence d'états (cachés) la plus probable ayant été générée par un modèle de Markov caché (problème de décodage). La reconnaissance de la parole et la bio-informatique utilisent abondamment les modèles de Markov cachés et sont donc aussi des domaines où l'algorithme de Viterbi trouve une application.

Exemple

Imaginons un canal bruité qui supprime tous les accents d'un texte. À partir du message m : « Université » on observe le message o : « Universite ».

Plusieurs messages ont pu conduire à cette observation :

• Ùnîvêrsîtê
• Ùnîvêrsîtè
• Ùnîvêrsîté
• ...
• Université
• ...

On peut connaître la probabilité de chaque lettre en s'intéressant à sa probabilité d'apparition dans la langue française et l'on peut affiner cette probabilité en cherchant la probabilité qu'une lettre apparaisse alors qu'elle est précédée d'une autre (et ainsi de suite), on parle d'unigrammes, de bigrammes, trigrammes...

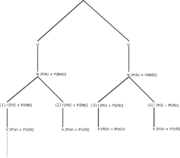
On construit l'arbre suivant (avec les bigrammes, P(X) correspond à la probabilité de voir apparaître X, P(Y/X) est la probabilité d'avoir Y sachant que l'on a eu X -- cf image).

La probabilité d'une branche est le produit de la probabilité de tous ses nœuds. À chaque nœud, on considère la probabilité de l'unigramme (P(X)) et du bigramme (P(X/Y)). Dans la pratique ces probabilités sont pondérées et normalisées et l'on obtient pour chaque nœud la valeur λ₁P(X) + λ₂P(Y / X) + λ₃P(Z / XY) + ... avec λ₀ + λ₁ + λ₂ + ... + λ_n = 1 (n correspondant au degré de n-gramme désiré), puisque l'on s'intéresse à une probabilité, donc comprise entre zéro et un (pour l'exemple, les valeurs λ₁ = 0.9 et λ₂ = 0.1 semblent optimales).

En regardant l'arbre, on se rend compte rapidement que les probabilités du troisième étage (pour le caractère observé « i ») sont identiques et ne dépendent que de l'étage précédent. De même, les sous-arbres de ces nœuds seront identiques, il est donc inutile de dérouler les sous-arbres sous les branches de plus faible probabilité puisque l'on est sûr que la probabilité totale des branches engendrées sera plus faible.

Par exemple, supposons que nous ayons obtenu comme probabilités au troisième étage de notre arbre :

• P(UNI) = 0.8
• P(UNÎ) = 0.15
• P(ÙNI) = 0.04
• P(ÙNÎ) = 0.01

Les sous-arbres en dessous du I de UNI et en dessous du I de ÙNI sont strictement équivalents, de même pour les sous-arbres en dessous du Î de UNÎ et du Î de ÙNÎ. On aura donc les probabilités suivantes :

• P(UNI...) = 0.8 * P(Sous-Arbre(NI)) (1)
• P(ÙNI...) = 0.04 * P(Sous-Arbre(NI)) (3)

et

• P(UNÎ...) = 0.15 * P(Sous-Arbre(NÎ)) (2)
• P(ÙNÎ...) = 0.01 * P(Sous-Arbre(NÎ)) (4)

Quelle que soit la probabilité de chacun des sous-arbres, on se rend compte que certains seront plus faibles que d'autres rapidement, par exemple la branche (4) sera inférieure à la branche (2) et la branche (3) inférieure à la branche (1). On peut donc élaguer l'arbre en les supprimant et continuer le calcul sur les branches restantes (suppression de la moitié des possibilités à chaque étape).

Références

• Error bounds for convolutional codes and an asymptotically optimum decoding algorithm, A Viterbi - IEEE Transactions on Information Theory, 1967. (papier fondateur de Viterbi)
• The Viterbi algorithm, GD Forney Jr - Proceedings of the IEEE, 1973.
• The Viterbi algorithm as an aid in text recognition (Corresp.) D Neuhoff - IEEE Transactions on Information Theory, 1975
• L. R. Rabiner. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE 77(2):257–286, February 1989.

Liens externes

• Une interview d'Andrew Viterbi, avec quelques détails sur la découverte de cet algorithme