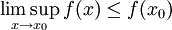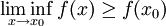Semi-continuite

En analyse mathématique, la semi-continuité est une propriété des fonctions à valeurs réelles ; il s'agit d'une forme faible de la continuité. Intuitivement, une fonction f à valeurs réelles est dite semi-continue supérieurement en x₀ si, lorsque x est proche de x₀, f(x) est soit proche de f(x₀), soit inférieure à f(x₀). Une fonction à valeurs réelles est dite semi-continue inférieurement si on remplace « inférieure à » par « supérieur à » dans la définition précédente.

Exemple

Une fonction semi-continue supérieurement (le point complètement bleu indique f(x₀)

Une fonction semi-continue inférieurement (le point complètement bleu indique f(x₀)

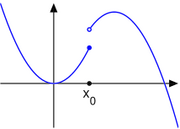
Considérons la fonction f(x) = -1 pour x < 0 et f(x) = 1 pour x ≥ 0. Cette fonction est semi-continue supérieurement, mais non semi-continue inférieurement.

La fonction partie entière 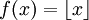, qui retourne le plus grand entier inférieur ou égal au x donné, est partout semi-continue supérieurement.

Définition formelle

Soit X un espace topologique, x₀ un point de X et f : X R une fonction à valeurs réelles. On dit que f est semi-continue supérieurement en x₀ si pour tout ε > 0, il existe un voisinage U de x₀ tel que f(x) < f(x₀) + ε pour tout x de U. De manière équivalente, on peut exprimer cela par :

où limsup est la limite supérieure (d'une fonction f au point x₀).

La fonction f est dite semi-continue supérieurement si elle est semi-continue supérieurement en tout point de son ensemble de définition. Une fonction est semi-continue supérieurement si et seulement si {x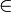X : f(x) < α} est un ouvert pour tout α.

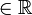De même, la semi-continuité inférieure en x₀ s'exprime par :

et la fonction est semi-continue inférieurement si elle est semi-continue inférieurement en tout point de son domaine de définition. Une fonction est semi-continue inférieurement si et seulement si {x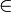X : f(x) > α} est un ouvert pour tout α.

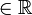Propriétés

Une fonction est continue en x₀ si et seulement si elle est semi-continue supérieurement et inférieurement.

Si f et g sont deux fonctions semi-continues supérieurement en x₀, alors f + g l'est aussi. Si aucune des deux fonctions n'est négative, leur produit fg est également semi-continue supérieurement en x₀. Multiplier une fonction semi-continue supérieurement par un nombre négatif donne une fonction semi-continue inférieurement.

Soit f_n : X R une suite de fonctions semi-continues inférieurement et

f(x) = sup {f_n(x) : n 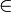N} < ∞

pour tout x dans X. Alors f est semi-continue inférieurement. Cette propriété subsiste non seulement pour les suites, mais également pour les familles quelconques de fonctions. Soit en effet 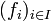une famille de fonctions semi-continues inférieurement. Alors pour tout réel λ > , l'ensemble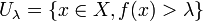

est la réunion des ensembles 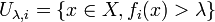 : c'est une réunion d'ouverts, il est donc lui-même ouvert.

Par contre, même si toutes les fonctions f_n sont continues, f n'est pas nécessairement continue.

La fonction indicatrice de tout ouvert est semi-continue inférieurement. La fonction indicatrice de tout fermé est semi-continue supérieurement.

Si C est un compact (par exemple un intervalle fermé [a,b]) et f : C R est semi-continue supérieurement, alors f est majorée sur C et atteint sa borne supérieure. La propriété est analogue pour les minima d'une fonction semi-continue inférieurement.

On peut démontrer que, dans un espace de Banach E, pour les fonctions f : E ]-∞,+∞], convexes, de domaine Dom(f) = {x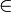E : f(x)<+∞} non vide et semi-continues supérieurement, f est continue en x si et seulement si x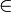Int(Dom(f)).

Semi-continuité faible

Dans le cas où X est un espace vectoriel topologique, on dit que la fonction f est faiblement semi continue (inférieurement ou supérieurement) lorsque la limite dans la définition de semi-continuité est prise au sens de la topologie faible. Afin d'éviter les ambiguïtés, on écrira parfois fortement semi continue pour désigner la semi-continuité définie pour la topologie forte.

• Portail des mathématiques