Theoreme du redressement

En mathématiques, le théorème du redressement d'un flot est un résultat de géométrie différentielle qui s'applique à un champ vectoriel. Il est l'un des théorèmes usuels en géométrie différentielle. Le théorème indique qu'un champ vectoriel suffisamment régulier se comporte localement comme un champ vectoriel constant.

Il est utilisé pour l'étude d'un système dynamique autonome, c'est-à-dire à une équation différentielle du type p' = X(p). Si X est localement lipschitzienne, alors il existe un fonction α(t, p) telle que les applications t -> α(t, p) soient les solutions qui, en 0, valent p. L'application α est appelée flot, d'où le nom du théorème.

Ce résultat donne une information locale sur le flot. Il interdit même une certaine forme de chaos : localement un flot ne bifurque pas et est homéomorphe à une fonction affine. En dimension deux, si une orbite se trouve dans un compact contenu dans l'ensemble de définition de X, toute forme de chaos est impossible. Ce résultat, connu sous le nom de théorème de Poincaré-Bendixson, se démontre à l'aide de ce théorème.

Sommaire 1 Énoncés 2 Explications 2.1 Vocabulaire 2.2 Interprétation 3 Démonstration 3.1 Construction de f 3.2 Propriété de la fonction f 4 Annexe 4.1 Notes 4.2 Références 4.3 Liens externes 4.4 Bibliographie

Énoncés

Selon le contexte, le théorème prend une forme différente. Une première version se formalise de la manière suivante. Soit E un espace de Banach réel, Ω un ouvert de E, X une application de classe C¹ de Ω dans E et p₀ un point de Ω tel que X(p₀) ne soit pas le vecteur nul.

• Théorème du redressement d'un champ de vecteurs dans un Banach : Si le champ de vecteurs X est de classe C^k, où k est un entier strictement positif ou l'infini, il existe un C^k difféomorphisme f d'un ouvert V dans un ouvert V' , tel que f(0) = p₀ et f ^* X soit le champ constant égal à X(p₀). Ici V' désigne un ouvert contenant p₀ et inclus dans Ω et V un ouvert d'un espace de Banach isomorphe à E et contenant le vecteur nul.^[1].

Ce théorème possède un équivalent pour les variétés différentielles :

• Théorème du redressement d'un champ de vecteurs dans une variété : Soit M une variété de dimension n et de classe C^k, où k est un entier strictement positif ou l'infini, et X un champ de vecteurs contenant un point p₀ de M. Si X(p) est un vecteur non nul, il existe une carte locale φ définie sur un ouvert V de Rⁿ tel que l'image de V par cette carte soit un ouvert U de M contenant p₀ et tel que l'image du champ de vecteur X par φ sur Rⁿ vérifie^[2] :

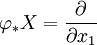
• Théorème des boites à flot : Soit U un ouvert contenant p₀ et inclus dans Ω. Il existe S une section transverse à X en p₀ inclus dans un hyperplan affine de direction H, un réel strictement positif σ et un difféomorphisme f défini sur un ouvert V, inclus dans U, et à valeurs dans Sx]-σ, σ[, qui envoie S dans Hx{0} et tel que le flot α(t, p) défini par X vérifie la propriété suivante^[3] :

Explications

Vocabulaire

Quelques symboles et termes nécessitent une explication. Le premier énoncé utilise le signe * dans une composition d'une fonction f et d'un champ de vecteurs X. Ici f est une application de V dans un ouvert inclus dans Ω. L'application qui à x associe X(f(x)) est bien définie sur X. Comme l'application f est un difféomorphisme, elle admet une différentielle au point x et cette différentielle est inversible. Ce qui assure que la définition suivante est bien cohérente :

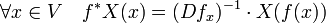
Pour éviter une débauche de parenthèses, ici l'image d'un vecteur v par une application linéaire a est notée a.v.

L'équation différentielle x' = X(x) admet toujours une unique solution s vérifiant s(0) = p^{[Note 1]}. La fonction qui à (t, p) associe α(t, p) définie comme la valeur de l'équation différentielle vérifiant la condition de Cauchy précédente est une fonction continue appelée flot. Si X est de classe C^k, alors le flot est aussi de classe C^{k[Note 2]}.

Un hyperplan H_a affine, de direction H contenant p₀ est dit transverse à X en p₀ si la somme directe de H et de R.X(p₀) est égal à E. Une section transverse à X est un ouvert S de H tel que l'hyperplan H_a soit transverse à X en tout point p de S. Si H_a est transverse à X en p₀, une section transverse contenant p₀ existe toujours. En effet, la composée de la projection sur R.X(p₀) parallèlement à H du champ X est non nulle en p₀ et est continue. Il existe un ouvert de p₀ sur lequel cette projection est supérieur à un nombre réel strictement positif. L'intersection de ce voisinage et de H_a, est une section transverse à X contenant p₀.

Interprétation

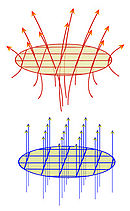
Ce théorème indique que localement et à un difféomorphisme près, on peut toujours considérer un champ de vecteurs comme constant. Le théorème redresse le champ à l'image de la figure de gauche. Un champ de classe C¹ est à l'image de la figure rouge et jaune, il est possible de lui appliquer un difféomorphisme à travers la loi de composition * qui lui donne l'apparence du champ bleu et jaune au dessous.

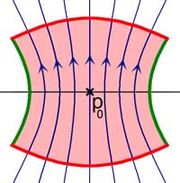
Une autre forme indique la possibilité de construire une boîte à flot. Dans le monde redressé, la boîte à flot ressemble à une boîte de conserve contenant en son milieu le point p₀. La base circulaire correspond à la section et le flot traverse la boite de sa base à son sommet à travers les trajectoires rectilignes uniformes et verticales. Ainsi, le flot ne rentre que par la base et ne sort que par le sommet, la paroi verticale est parallèle au flot et n'est pas traversée par lui. Dans le monde original, la boîte à flot est déformée par le difféomorphisme, mais garde cette propriété, la base reçoit le flot entrant, le sommet le flot sortant et la paroi reste parallèle au flot, à l'image de la figure de droite. Une telle boîte permet un contrôle du flux au voisinage de p₀.

Un exemple d'usage d'une boîte à flot est la démonstration du théorème de Poincaré-Bendixson. Une telle boîte permet le contrôle de la trajectoire aux alentours d'un point bien choisi. A l'aide du théorème de Jordan, elle permet d'établir l'impossibilité d'une configuration chaotique si E est un plan, si l'équation différentielle est autonome dans une zone compacte de Ω invariante par le flot.

Démonstration

La démonstration se fonde essentiellement sur l'usage du théorème d'inversion locale et des propriétés d'un flot d'une équation différentielle. La démonstration se fait en deux temps. Tout d'abord, une fonction affine q est composée à X de manière à ce que le champ de vecteurs q ^*X ait pour différentielle l'identité au voisinage du vecteur p₀. Comme le champ X est de classe C^k et q infiniment différentiable, le nouveau flot est de classe C^k-1 et le théorème d'inversion locale s'applique. Il existe un ouvert V contenant p₀ tel que le flot soit inversible. Ce flot permet la construction de la fonction f recherchée^[4].

La démonstration sur un espace vectoriel permet d'en déduire immédiatement celle associée à une variété^{[Note 3]}.

Construction de f

Soit λ₁ la forme linéaire définie sur R.X(p₀) qui à a.X(p₀) associe a, λ un prolongement linéaire continu de λ₁ sur E, qui existe d'après un corollaire du théorème de Hahn-Banach et H l'hyperplan noyau de λ, qui est fermé car λ est continue. Soit π, la projection de E sur H, qui à x associe π(x) = x - λ(x).X(p₀). On définit la fonction q, de RxH dans E par :

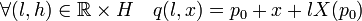
On remarque que q est bien un difféomorphisme infiniment différentiable, car q est une application affine. On dispose des égalités :

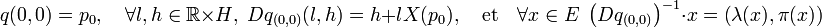
On en déduit l'égalité, si Y désigne le champ de vecteurs q^* X :

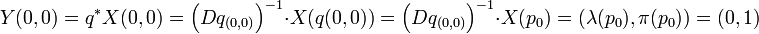
Soit α_Y le flot associé à l'équation différentielle (τ, x)' = Y((τ, x)). C'est l'application qui à (t, (τ, x)) associe α_Y(t, (τ, x)), l'image de t par la courbe intégrale s de condition initiale s(0) = (τ, x). Comme X est de classe C^k, Y l'est aussi (q est infiniment différentiable) et le flot α_Y est de classe C^{k-1[Note 4]}. On considère alors l'application Ψ, qui à (t, x)) associe Ψ(t, x)) = α_Y(t, (0, x)). Cette application est de classe C^k-1 et est définie sur un ouvert V₁ contenant (0, 0).

Il est aisé de calculer les deux différentielles partielles :

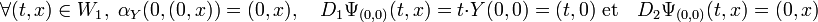
On en déduit que la différentielle de Ψ est égal à l'identité au point (0, 0). Ce qui montre qu'il existe ouvert V contenant (0, 0) et inclus dans V₁ et tel que Ψ soit un difféomorphisme sur V, d'après le théorème d'inversion locale. On définit f comme la fonction définie sur V, égale à qoΨ.

Propriété de la fonction f

Soit (t, x) un élément de V, Calculons la différentielle de DΨ_(t,x) appliquée au vecteur (1, 0) :

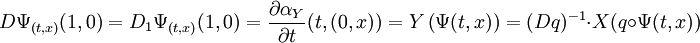
On en déduit l'égalité, en appliquant l'inverse de DΨ_(t,x) à l'égalité précédente :

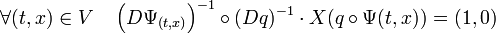
Calculons l'inverse de la différentielle de f au point (t, x) :

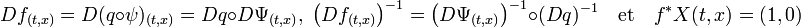
Annexe

Notes

Références

Liens externes

• (fr) F. Paulin Topologie, analyse et calcul différentiel par l'École Normale Supérieure

Bibliographie

• (en) M. W. Hirsch S. Smale Differential Equations, Dynamical Systems, and an Introduction to Chaos Academic Press (2002) (ISBN 0123497035)
• (fr) D. Leborgne Calcul différentiel et géométrie Puf (1982) (ISBN 2130374956)

• Portail de la géométrie