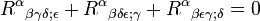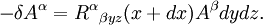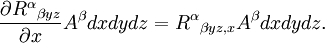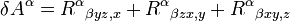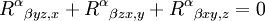- Identites de Bianchi
-
Identités de Bianchi
Les identités de Bianchi sont des équations satisfaites par le tenseur de Riemann
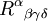, objet mathématique qui reflète la courbure de la variété riemannienne sur laquelle il est calculé.Seconde identité de Bianchi
Celle-ci est le pendant, pour le tenseur de Riemann, des équations de Maxwell pour le tenseur électromagnétique
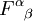. Rappelons que le premier groupe d'équations de Maxwell s'écrit :- Fαβ;γ + Fβγ;α + Fγα;β = 0
De même, la seconde identité de Bianchi s'énonce comme :
Comme
![{R^{\alpha}}_{\beta \gamma \delta} = {R^{\alpha}}_{\beta [\gamma \delta]}](/pictures/frwiki/55/74c290c796075a4390ca2f2cb3c6c756.png)
, cette identité peut se noter sous une forme « condensée » : ![{R^{\alpha}}_{\beta [\gamma \delta;\epsilon]} = 0](/pictures/frwiki/53/5dafd1d96183528b36777c8cb6fa8159.png)
Interprétation
Pourquoi l'identité de Bianchi ? (Schéma d'après Misner, Thorne et Wheeler, Gravitation, p. 372)
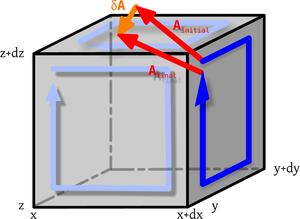
La figure à gauche aide à comprendre le pourquoi de l'identité de Bianchi. Lorsque, dans un espace courbe, le vecteur A est déplacé parallèlement à lui-même le long d'une des faces du cube élémentaire de dimensions {dx, dy, dz}, suivant l'une des flèches en bleu, il ne revient pas, en général, égal à lui-même à son point de départ, mais subit une « déformation » notée ici δA.
Dans le cas de la flèche bleu sombre, au premier ordre, on peut écrire que ce déplacement δA vérifie :
La face opposée apporte une contribution opposée, à ceci près que
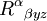est maintenant évalué en x plutôt qu'en x + dx. La somme de ces deux contributions donne :Le même raisonnement conduit sur la face située en haut (en z + dz) et en arrière (y + dy) donne la même équation en échangeant les rôles de x, y et z. Au total, en considérant les 3 doublets de faces opposées, on trouve :
Examinons maintenant la figure. Lorsque le vecteur A parcourt les six faces du cube, on voit que chaque arête est parcourue une fois dans un sens, et une fois dans l'autre (chaque face étant orientée ici dans le sens des aiguilles d'une montre). Les contributions élémentaires de chaque arête s'annulent donc deux à deux (car le tenseur de Riemann est un opérateur linéaire !). Ceci implique que la valeur totale de δA sur l'ensemble du cube est nulle (« la frontière d'une frontière est de mesure nulle »).
On a donc, au final :
c'est-à-dire l'identité de Bianchi. Le passage de la dérivée simple « , » à la dérivée covariante « ; » s'opère en considérant que l'on raisonne avec les coordonnées normales de Riemann, où les coefficients de Riemann-Christoffel s'annulent (
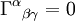), donc « , » = « ; ».Catégorie : Géométrie riemannienne
Wikimedia Foundation. 2010.
