Scilab

Scilab
Développeur	Digiteo / Consortium Scilab
Dernière version	5.3.2 (12 mai 2011) [+/-]
Version avancée	[+/-]
Environnements	Linux, Windows, Mac OS X, BSD.
Type	Calcul numérique
Licence	CeCILL v2
Site web	www.scilab.org
modifier

Scilab (prononciation : [sajlab]^{[réf. nécessaire]}) est un logiciel libre de calcul numérique multiplate-forme fournissant un environnement de calcul pour des applications scientifiques. Il possède un langage de programmation orienté calcul numérique de haut niveau. Il peut être utilisé pour le traitement du signal, l'analyse statistique, le traitement d'images, les simulations de dynamique des fluides, l'optimisation numérique, et la modélisation et simulation de systèmes dynamiques explicites et implicites.

Développé depuis 1990 par des chercheurs de l’INRIA et de l’ENPC, il est développé par le Consortium Scilab depuis mai 2003, Consortium développé et maintenu par l'INRIA jusqu'en juillet 2008 puis depuis par la Fondation de coopération scientifique Digiteo.

Il est disponible pour Windows, Mac OS X, Linux et BSD.

La syntaxe et les possibilités offertes par Scilab sont similaires à celles de Matlab, mais les deux logiciels ne sont pas compatibles bien qu'un traducteur de Matlab vers Scilab existe.

Licence

Mascotte de Scilab^[1] représentant un macareux.

Distribué gratuitement et avec son code source via l’Internet depuis 1994, il est disponible précompilé pour un grand nombre d’architectures. Néanmoins, il ne s’agissait ni d’un logiciel Open source selon l'Open Source Initiative ni d’un Logiciel libre. En effet, l'ancienne licence Scilab^[2] n’autorise pas la distribution commerciale d’une version modifiée. Selon la classification de la FSF, il s'agissait donc plutôt d'un logiciel semi-libre^[3]. Scilab est donc devenu un logiciel libre lors du changement de licence : il est distribué sous la licence CeCILL v2 depuis la version 5.0, licence libre compatible GNU GPL^[4].

Présentation succincte de l’utilisation

Scilab peut exécuter des instructions en ligne de commande, ainsi que des fichiers de commande (scripts) contenant des instructions (format texte). On peut également exécuter des programmes Fortran ou C à partir de Scilab. Scilab est complété par un environnement graphique Xcos (basé sur Scicos) comparable à l'environnement graphique Simulink fourni avec Matlab.

Syntaxe élémentaire en ligne de commande

L’invite de la ligne de commande (prompt) est constituée d’une « flèche » : deux tirets et un signe supérieur -->. L’instruction est tapée puis validée avec la touche de retour chariot (Enter, Return). Le résultat est affiché à la suite, sauf si la ligne se termine par un point-virgule auquel cas le résultat est caché. Par exemple :

 -->a = 1;
 -->A = 2;
 -->a + A
 ans =
 
 3.

La première commande associe la valeur « 1 » à la variable « a » (résultat caché), la seconde commande associe la valeur « 2 » à la variable « A » (la syntaxe est sensible à la casse), la troisième commande calcule la somme des deux (ans est l’abréviation de answer qui signifie « réponse » en anglais).

On peut écrire plusieurs instructions sur la même ligne en les séparant d’une virgule, ou d’un point-virgule si l’on ne veut pas en afficher le résultat. On peut aussi mettre une instruction sur plusieurs lignes (par exemple pour des raisons de présentation) en mettant trois points « ... » avant de presser la touche de retour chariot.

Scilab utilise les fonctions et opérateurs classiques (+, -, *, /, ^ ou **, sqrt() pour la racine carrée, cos() pour le cosinus, int() pour la partie entière, round() pour l’arrondi au plus proche, abs() pour la valeur absolue…) et quelques autres (par exemple rand pour avoir un nombre aléatoire entre 0 et 1). La fonction who affiche les variables déclarées. La variable ans contient le dernier résultat.

Le séparateur décimal est le point. Pour entrer l’imaginaire i, il faut utiliser %i ; il figure simplement sous la forme « i » dans les résultats. Pour entrer l’infini ∞, il faut utiliser %inf ; il figure simplement sous la forme « inf » dans les résultats. La valeur de π s’obtient par %pi, et la constante de Neper e par %e.

Booléens

Lorsque l’on assigne une valeur booléenne, on utilise %T pour « vrai » (true) et %F pour « faux » (false). Le résultat de l’opération affiché est respectivement T ou F.

L’opérateur Ou est noté « | » (tube), Et est noté « & » (esperluette), Non est noté « ~ » (tilde). Exemple

-->(%T & %F) | %F
ans =
 
F.

Un booléen peut également s’obtenir en comparant deux valeurs, avec les relations d’égalité == et de différence <> ou ~=, et les relations d'ordre <, <=, > et >=.

Polynômes et fractions rationnelles

Il s’agit ici non pas de fonctions polynômes qui ne permettraient que leur évaluation numérique, mais de polynômes formels.

La déclaration d’un polynôme se fait avec deux fonctions. La première fonction, x = poly(0, 'x') qui définit « x » comme l’indéterminée d’un polynôme, puis l’énoncé du polynôme utilisant cette indéterminée. Exemple

-->x = poly(0, 'x'); p = x ^ 2 + 2 * x + 1
p =
 
          2
1 + 2x + x

La fonction roots(p) donne les racines du polynôme p, la fonction coeff(p) donne une matrice dont les coefficients sont les coefficients du polynôme p. La fonction varn(p) renvoie le nom de l’indéterminée de p (ici, x).

En fait, la commande x = poly(0, 'x') définit que x est le polynôme le plus simple dont l’indéterminée est le caractère « x » et dont la racine est 0, c’est-à-dire le monôme x. La commande x = poly(2, 'x') définit de même le polynôme le plus simple ayant pour racine 2, c’est-à-dire x - 2.

Cette fonction permet de définir un polynôme ayant plusieurs racines, en utilisant une matrice ligne au lieu d’un simple nombre. Par exemple, x=poly([1 2],'x') définit le polynôme le plus simple ayant pour racines 1 et 2, soit le polynôme x² - 3x + 2.

On peut aussi utiliser cette fonction pour générer un polynôme dont les coefficients sont contenus dans une matrice ligne, en ajoutant le caractère 'c' à la fin des arguments. Par exemple, x = poly([a0, a1, …, an], 'x', 'c') définit le polynôme a0 + a1·x + … + an·xⁿ.

Scilab gère de la même manière les fractions rationnelles. Il suffit de déclarer un monôme avec poly() et définir ensuite la fraction rationnelle. Exemple

-->x = poly(0, 'x'); f = (1 + x) / (1 - x)
f = 
 
1 + x
-----
1 - x

-->1/f
ans =
 
1 - x
-----
1 + x

Pour avoir le numérateur de f, il suffit de taper f.num ; le dénominateur de f s’obtient avec f.den.

La fonction derivat(p) donne la dérivation formelle du polynôme ou d’une fraction rationnelle p. La fonction simp(q) fait la simplification de la fraction rationnelle q.

L’utilisation du polynôme ou d’une fraction rationnelle en tant que fonction se fait par la fonction horner : horner(p,2) calcule p(2).

Caractère

Les caractères isolés ou les chaînes de caractères sont notés entre apostrophes simples, ou bien entre guillemets : 'abc' ou "abc".

L'apostrophe indique la fin d'une chaîne ; pour mettre une apostrophe dans une chaîne, il faut en écrire deux accolées ''.

L’addition + sur des chaînes de caractères produit la concaténation. Une chaîne de caractère peut être évaluée, c’est-à-dire transformée en commande Scilab, par la fonction evstr().

Matrices

Scilab a été conçu pour le calcul matriciel. Toutes les fonctions s’appliquent à des matrices ; par exemple si M est une matrice, alors log(M) sera la matrice dont les coefficients sont les logarithmes des coefficients de M. Les éléments des matrices peuvent être de tout type (nombre réel, nombre complexe, booléen, polynôme, fraction rationnelle, chaîne de caractères…).

Pour définir une matrice à partir de ses coefficients, on les place entre deux crochets […]. Les éléments d’une ligne sont séparés d’un espace ou d’une virgule, les lignes sont séparées d’un point-virgule. À l’affichage, la matrice est représentée comme un tableau encadré par des points d’exclamation. Par exemple :

-->[1,2,3;0,1,0;0,0,1]
ans =
 
! 1. 2. 3. !
! 0. 1. 0. !
! 0. 0. 1. !

La matrice vide est notée par []. L’expression M(i,j) désigne l’élément (i, j) de la matrice M. Le caractère : (deux-points) signifie « tous les indices », par exemple M(1, :) est la première ligne de la matrice (c’est un vecteur ligne). Le caractère $ (dollar) désigne le dernier indice (ligne ou colonne) d’une matrice.

L’expression N1:N2 permet de générer une matrice-ligne dont le premier coefficient est N1, le dernier est inférieur ou égal à N2, et le pas entre les coefficients est 1. L’expression N1:pas:N2 permet de générer une matrice-ligne en choisissant le pas. Par exemple

-->1.1:5.2
ans = 
 
! 1.1 2.1 3.1 4.1 5.1 !
 
--> 1:2:5
ans =
 
! 1 3 5 !
 
-->'a' :'d'
ans =
 
abcd

La fonction zeros(m,n) crée une matrice m×n remplie de 0 ; la fonction ones(m,n) crée une matrice m×n remplie de 1. La fonction eye(n,n) crée une matrice unité n×n. On peut aussi passer une matrice M en paramètre de ces fonctions ; elles créent alors une matrice de même dimension que la matrice M. Par exemple, M=zeros(M) met tous les coefficients de M à zéro.

Si f est une fonction extérieure (c’est-à-dire définie par deff ou par function, voir ci-après), et que x et y sont des vecteurs, alors la fonction feval permet de bâtir une matrice z = f(x, y)

z = feval(x, y, f) : on a z(i, j) = f(x(i), y(j))

La fonction size(M) renvoie la taille de la matrice sous la forme d’une matrice 2×1 contenant le nombre de lignes puis le nombre de colonnes.

Les opérations spécifiques aux matrices classiques sont :

• la transposition : il suffit de mettre une apostrophe ’ après la matrice ;
• le produit de matrices : * ;
• produit et rapport élément par élément : .* et ./ ;
• le produit tensoriel .*. ;
• le déterminant d’une matrice carrée M : det(M) (determ() pour une matrice de polynômes et detr() pour une matrice de fraction rationnelle) ;
• la trace d’une matrice carrée M : trace(M) ;
• l’inverse d’une matrice inversible M : inv(M).

Un vecteur est une matrice ligne ou colonne (matrice 1 × n ou n × 1) ; l’expression V(i) désigne la composante i du vecteur V. Si V1 et V2 sont des vecteurs colonnes, alors le produit scalaire est V1' * V2 ; si ce sont des vecteurs lignes, le produit scalaire est V1 * V2'.

Calcul numérique

Scilab peut effectuer des calculs numériques.

On peut en faire une utilisation triviale comme calculatrice, en entrant simplement les opérations à effectuer.

La fonction deff permet de définir de nouvelles fonctions (appelées « fonctions externes ») pouvant s’exprimer avec les opérateurs déjà prédéfinis (les « fonctions primitives »). On passe deux chaînes de caractères comme paramètre ; la première indique le nom de la fonction et les variables utilisées en entrée et en sortie, et la deuxième indique la formule. Par exemple, la fonction

f(x) = 2 · x

peut se définir par

deff('[y] = f(x)', 'y = 2 * x')

(voir aussi la section Programmation).

Intégration

integrate('expression', 'x', x0, x1) calcule l’intégrale de la fonction décrite par expression (c’est une chaîne de caractères interprétable par Scilab, comme par exemple 'sin(x)'), x étant la variable d’intégration, entre les valeurs x0 et x1.

Résolution d'équations

Scilab dispose de plusieurs primitives permettant la résolution d'équations (voir Solveur d'équations), entre autres :

• linsolve : résolution d'un système d'équations linéaires,
  syntaxe : [x0,kerA]=linsolve(A,b)
  où A est la matrice réelle des coefficients du système d'équations, et b un vecteur de constantes ; les solutions de A×x + b = 0 sont de la forme x0 + w×kerA, w étant un réel arbitraire ;
• solve : résolution symbolique d'un système linéaire,
  syntaxe : w = solve(A,b)
  où A est une matrice triangulaire supérieure de caractères (les coefficients du système d'équation), b est un vecteur de caractères (la partie à droite des signes égal), et w est la matrice résultat de A×w = b ;
• ode : résolution d'une d'équation différentielle ordinaire (ordinary differential equation) ; si l'équation différentielle est dy/dt = ƒ(t), alors ƒ ayant été définie (fonction externe), la syntaxe pour déterminer y(t) est
  y = ode(y0,t0,t,f)
  où y0 et t0 sont les valeurs initiales du système, t est un vecteur de valeurs pour lesquelles on calcule les solutions, et y est le vecteur de solutions (plot(t,y) permet de tracer le graphique des solutions) ;
  la primitive ode admet des arguments permettant de résoudre des situations spécifiques : 'roots' pour rajouter une équation g(t, y) = 0, 'discrete' pour calculer de manière récursive y(k+1)=ƒ(k,y(k)) à partir d'un état initial y(k0).

Il existe d'autres primitives pour des systèmes spécifiques.

Tracé de fonction

Tracé 2D

Le tracé d’une fonction se fait en deux étapes

1. définir l’étendue de la variable abscisse et le pas, sous la forme d’un vecteur colonne, par exemple x = [début:pas:fin]' ;
2. tracer la fonction avec la commande plot(x, f(x)) si ƒ est la fonction.

On peut tracer simultanément plusieurs fonctions en les mettant dans une matrice, par exemple plot(x, [f1(x) f2(x) f3(x)]).

On note en fait que ƒ(x) est elle-même un vecteur. On peut de manière générale définir un vecteur des valeurs de x et un vecteur des valeurs de y, et la fonction plot(x, y) tracera le nuage de points.

Si ƒ est une fonction externe (par exemple définie avec deff, voir ci-dessus, ou function, voir ci-après), alors on peut tracer directement la fonction avec fplot2d(x, f). On peut aussi définir y par y = feval(x, f), puis tracer avec plot(x,y).

La fonction xgrid permet d’afficher une grille correspondant aux graduations.

Les fonctions plot2di, utilisées à la place de plot, permettent de faire varier l’apparence générale du tracé :

• plot2d : trait « normal » ; identique à plot, mais permet l’utilisation de marqueurs ;
• plot2d2 : trait en escalier ;
• plot2d3 : tracé en barres ;
• plot2d4 : tracé en « flèches » (pour un champ de vecteurs) ;

Ces fonctions plot2di acceptent des arguments modifiant le tracé, sous la forme plot2di(x, y, arguments). Les arguments sont de la forme mot-clef = valeur, et sont séparés par des virgules.

Pour placer des marqueurs, on utilise l’argument style = n ou n est un entier positif ou négatif (par exemple plot2d(x, y, style = 1)) ; un nombre négatif remplace les points par des marqueurs (une étoile pour -10, des ronds pour -9, …, des petits points pour 0, la liste s'obtient en tapant la commande getsymbol) et un nombre positif indique un trait plein mais de couleur déterminée (selon la carte de couleur définie, voir ci-après).

Si le tracé comporte plusieurs courbes (donc mis dans une matrice ligne Y), l’argument style est une matrice, la valeur de chaque élément indiquant le style de chaque courbe, par exemple

Y = [cos(x), sin(x)]; plot2d(x, Y, style = [-2, -1])

Dans ce cas-là, on peut inscrire une légende sous le graphique pour chaque symbole, avec l’argument leg = ('texte1@texte2'), l’arobase servant à séparer les légendes, par exemple

plot2d(x, Y, style = [-2, -1], leg = 'cosinus@sinus')

Pour une échelle logarithmique, on utilise l’argument logflag = type où type est une chaîne de deux caractères, « n » (pour normal) ou « l » (pour logarithmique), le premier caractère correspondant à l’axe des x et le second à l’axe des y. Par exemple

• plot2d(x, y, logflag = 'nl') pour un axe des x linéaire et un axe des y logarithmique ;
• plot2d(x, y, logflag = 'll') pour avoir deux échelles logarithmiques.

On peut choisir le type d’axe avec l’argument axesflag=n où n est un entier positif : 0 pour ne pas avoir d’axe, 1 pour des axes « classiques » se recoupant en bas à droite, 4 pour des axes « classiques » se coupant au centre, 5 pour des axes se coupant en (0, 0)…

On peut définir le nombre de graduations et de sous-graduations des axes avec l’argument nax = [nx, Nx, ny, Ny] où Nx est le nombre de graduations de l’axe x, nx le nombre de sous-graduations…

L’argument rect = [xmin, ymin, xmax, ymax] permet de limiter le tracé à la zone comprise dans le rectangle défini par les valeurs dans la matrice.

La fonction polarplot réalise un tracé en coordonnées polaires. La fonction r(theta) se trace par la commande :

polarplot(r,theta)

où r et theta sont deux matrices de même dimension.

Carte d’un champ

Si x est un vecteur colonne de m éléments, y un vecteur colonne de n éléments et z une matrice m×n, alors la fonction

grayplot(x, y, z)

va associer une couleur à chaque valeur de z et tracer une carte de couleurs, chaque point (x(i), y(j)) ayant la couleur associée au coefficient z(i, j).

Les niveaux de couleur sont indiqués par la fonction

xset('colormap', cmap)

où cmap est une matrice de trois colonnes dont chaque ligne contient la couleur associée à un niveau, sous la forme RVB (les éléments de la matrice allant de 0 à 1). La première ligne de la matrice correspond au plus bas niveau, la dernière ligne au plus haut. Cette matrice peut être générée de manière automatique par les fonctions colormap :

graycolormap(n), où n est un entier, génère n niveaux de gris entre le noir et le blanc ;

jetcolormap(n), où n est un entier, génère n niveaux de couleur entre le bleu et le rouge ;

hotcolormap(n), où n est un entier, génère n niveaux de couleur entre le rouge et le jaune.

On peut par exemple utiliser xset('colormap',graycolormap(32)) pour avoir 32 niveaux de gris. On peut réaliser un dégradé du noir vers le rouge avec

cmap = graycolormap(32); cmap(:, 2:3) = 0 ou avec r = [0:32 / 31:32]' / 32; cmap = [r zeros(32, 2)]

et un dégradé du bleu vers le blanc avec

cmap = graycolormap(32); cmap(:, 2:3) = 1 ou avec r = [0:32 / 31:32]' / 32; cmap = [r ones(32, 2)]

Les niveaux de couleur sont également utilisés lorsque l’on trace plusieurs courbes sur le même graphique. Dans ce cas-là, des dégradés ne fournissent pas un contraste permettant de distinguer facilement des courbes voisines ; on peut obtenir les niveaux de couleur par défaut avec get(sdf(), 'color_map').

On peut tracer une courbe de niveaux avec la fonction

contour2d(x, y, z, n)

où n est le nombre de niveaux que l’on veut voir figurer ; on peut aussi donner les valeurs des niveaux z₁, z₂, …, z_n par un vecteur

contour2d(x, y, z, [z1,z2,...,zn])

On peut également tracer un champ de vecteurs. Pour cela, il faut une matrice vx ayant les composantes selon x du champ de vecteur, une matrice vy ayant les composantes selon y de ce champ, et utiliser la fonction

champ(x, y, vx, vy)

Avec la fonction champ1, les vecteurs tracés ont tous la même longueur, la norme du champ est indiquée par la couleur du vecteur, suivant le principe exposé pour grayplot.

Tracé 3D

Scilab permet également le tracé de surfaces à trois dimensions (x, y, z). Si x est une matrice colonne de m éléments, y une matrice colonne de n éléments, et z une matrice m×n, alors la fonction

plot3d(x, y, z)

va tracer la surface des points (x(i), y(j), z(i, j)). S’il s’agit d’une surface représentative d’une fonction ƒ, on a

z(i, j) = f(x(i), y(j)).

Si ƒ est une fonction « externe » (par exemple définie par deff ou function), on peut définir z avec la fonction feval (voir plus haut), ou bien utiliser fplot3d(x, y, f).

La fonction param3d(fx(t), fy(t), fz(t)) trace la courbe paramétrique ; t est un vecteur contenant les valeurs successives du paramètre.

Les fonctions plot3d1, fplot3d1 et param3d1 permettent d’utiliser des niveaux de couleurs pour indiquer la valeur de z. L’utilisation est identique à celle de plot3d, mais les niveaux de couleur sont indiqués par la fonction

xset('colormap', cmap)

(voir ci-dessus).

Le point de vue de la surface 3D est défini par deux angles en degrés, θ, rotation autour de l’axe des Z, et α, rotation autour de l’axe des Y (voir aussi Angles d'Euler) : plot3d(x, y, z, theta, alpha), param3d(x, y, z, theta, alpha)… ;

• plot3d(x, y, z, 0, 0) donne une vue de dessus, semblable aux cartes 2D, projection de la surface sur le planXY selon l’axe Z ;
• plot3d(x, y, z, 90, 0) donne une vue de face, projection de la surface sur le planXZ selon l’axe Y ;
• plot3d(x, y, z, 0, 90) donne une vue de côté, projection de la surface sur le planYZ selon l’axe X ;
• plot3d(x, y, z, 45, 45) est la vue par défaut, de type perspective isométrique.

On peut également définir les limites des axes avec le mot-clef ebox :

• plot3d(x, y, z, ebox=[xmin, xmax, ymin, ymax, zmin, zmax])
• plot3d(x, y, z, theta, alpha, ebox=[xmin, xmax, ymin, ymax, zmin, zmax])

Représentation de données statistiques

Si x est un vecteur, la fonction histplot(n, x), n étant un entier, va découper l’intervalle de valeurs prises par les coefficients de x en n tranches d’égale largeur, et tracer l’histogramme de répartition des valeurs selon ces tranches. Si n est un vecteur dont les coefficients sont strictement croissants, les valeurs des coefficients de n servent à déterminer les tranches.

Si x est une matrice, hist3d(x) trace un histogramme 3D tel que le parallélépipède situé en (i, j) a pour hauteur x(i, j). Comme pour toutes les fonctions de tracé en trois dimensions, on peut définir l’angle de vue avec θ et α.

Dessin

Il est possible de dessiner directement des figures géométriques sur le graphique.

La fonction xpoly(x,y,'lines',1) permet de tracer un polygone fermé, x étant la liste des abscisses des sommets (sous la forme d'un vecteur ou d'une matrice) et y étant la liste des ordonnées des sommets (c'est une matrice de même dimension que x). La fonction xfpoly(x,y,'lines',1) permet de tracer un polygone rempli.

La fonction xrect(x,y,l,h) trace un rectangle dont le point en haut à gauche est (x, y), de largeur l et de hauteur h. La fonction xfrect(x,y,l,h) trace un rectangle rempli.

La fonction xstring(x,y,'chaîne') écrit la chaîne de caractère chaîne sur le graphique, le point en bas à gauche du texte étant au point (x,y).

La fonction xarc(x,y,l,h,a1,a2) trace un arc d'ellipse compris dans le rectangle dont le point en haut à gauche est (x, y), de largeur l et de hauteur h. Chaque degré d'angle est divisé en 64 secteurs, l'arc part de l'angle trigonométrique a1×64 ° et va jusqu'à l'angle (a1+a2)×64 °. La fonction xfarc(x,y,l,h) trace un arc d'ellipse rempli.

Pour changer les propriétés des traits des dessins, il faut utiliser la commande set('propriété',valeur). Les principales propriétés d'un objet sont :

• line_style : type de trait ; c'est un entier, 0 pour un trait plein, 2 pour des pointillés longs, trois pour des pointillés courts, 4 pour un trait d'axe (alternance trait-point)…
• thickness : épaisseur du trait, sous la forme d'un entier positif ;
• mark_size : dans le cas d'un tracé par marqueurs, taille des marqueurs.

On peut aussi associer une variable à l'élément dessiné ; cela se fait avec la fonction
variable = get('hdl')
hdl signifiant handle (littéralement « poignée », intermédiaire d'action). Pour définir la propriété de cet élément, on fait

variable.propriété = valeur

Ces deux méthodes sont valables quel que soit l'objet (courbe, polygone, arc d'ellipse…).

Par exemple

xarc(0,1,0.5,0.5,0,360*64) // ellipse
set('line_style', 2) // pointillés

ou bien

xarc(0,1,0.5,0.5,0,360*64) // ellipse
a=get('hdl')
a.line_style=2 // pointillés

Mise en forme, axes et fenêtrage

La fonction xset permet de définir l’apparence :

• police des graduations et titres : xset('font', type, taille), où
  • taille est un nombre désignant la taille des caractères, en unité arbitraire ;
  • type est un nombre désignant le type de police : 1 pour les lettres grecques (police Symbol), 2–5 pour une police avec empattements type Times (2 pour des lettres romanes, 3 en italique, 4 en gras, 5 en gras italique) ; 6–9 pour une police sans empattement type Arial (6 pour des lettres romaines, 7 en italique, 8 en gras, 9 en gras italique) ;
• épaisseur des traits d’axe et du tracé : xset('thickness', e) où e est un nombre désignant l’épaisseur en unité arbitraire ;
• taille des marqueurs (le cas échéant, voir ci-après) avec xset('mark size', taille).

Comme pour tous les objets graphiques, on peut changer les propriétés des axes en les affectant à une variable par la commande var=get('current_axes'). Les principales propriétés sont :

• x_location et y_location : prennent les valeurs 'top', 'middle' ou 'bottom' selon que l'on veut que l'axe soit en haut, passe par l'origine, ou soit en bas ;
• isoview : vaut 'on' si l'on veut que les échelles soient identiques sur les axes, 'off' si l'échelle est libre ;
• sub_ticks : matrice [nx,ny] où nx et ny est le nombr ede sous-graduation (il faut 4 sous-graduations pour que la graduation principale soit divisée en 5) ;

Exemple

a=get('current_axes')
a.x_location='middle'
a.y_location='middle'
a.isoview='on'
a.sub_ticks=[4,4]

On peut placer plusieurs tracés côte à côte avec l’instruction subplot :

subplot(m, n, i) place le tracé qui suit l’instruction dans la i ^e case (dans l’ordre de lecture européen) d’un tableau m×n ; le tracé peut comporter plusieurs instructions plot, xset, xtitle.

La fonction xtitle('nom du graphique','axe des x', 'axe des y') met un titre au graphique et aux axe. La fonction titlepage('titre') met un titre au milieu du graphique. La fonction clf efface la fenêtre graphique.

Exemple

Exemple de graphique obtenu avec Scilab

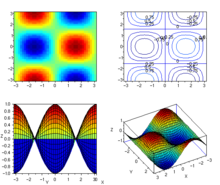
Voici le graphique que l’on obtient avec les instructions ci-dessous.

clear; clf;
 
deff('[z] = f(x, y)', 'z = sin(x) * cos(y)')
 
xset('colormap', jetcolormap(32))
 
x = %pi * [-1:0.05:1]';
y = x;
z = feval(x, y, f);
 
subplot(2, 2, 1)
grayplot(x, y, z)
 
subplot(2, 2, 2)
contour2d(x, y, z, 5)
 
subplot(2, 2, 3)
plot3d1(x, y, z, 0, 90)
 
subplot(2, 2, 4)
plot3d1(x, y, z, 70, 70)

Programmation

Scilab accepte un certain nombre d’instructions :

• exécution conditionnelle if condition then, …, else, …, end
• boucle itérative for variable = début : fin, …, end ou for variable = début : pas : fin, …, end
• boucle itérative antéconditionnée : while condition do, …, end ou while condition do, …, else, …, end

Il est possible de définir des fonctions avec passage de paramètres. La fonction est un sous-programme avec ses variables propres, et qui peut contenir des boucles, des branchements conditionnels... Par exemple, pour définir une fonction f(x) :

-->function [y] = f(x)
--> …
--> endfunction

Le paramètre x est passé à la fonction f ; la valeur retournée par f sera celle qui est attribuée à y dans la fonction.

On peut enregistrer l’environnement, c’est-à-dire l’ensemble des variables, dont notamment les fonctions, avec la commande save('fichier'). Ceci crée un fichier binaire (Scilab n’ajoute pas d’extension). Cet environnement peut être rechargé avec la fonction load('fichier').

On peut également écrire les instructions dans un fichier texte, puis faire du copier/coller depuis l’éditeur de texte vers la ligne de commande de Scilab. Le code source peut contenir des commentaires introduits par deux barres de fraction //.

Environnement

Dans Scilab, l’environnement est l’ensemble des variables (y compris les fonctions) qui ont été définies ; l’environnement contient un certain nombre de variables prédéfinies. L’ensemble des variables est donné par la commande who.

Lorsque l’on utilise une fonction, l’exécution de la fonction se fait dans un nouvel environnement, copie de l’environnement initial. Les variables qui y sont modifiées ne le sont pas dans l’environnement initial (on ne travaille qu’en variables locales), seul le résultat de la fonction est renvoyé.

On peut ouvrir à dessein un environnement, avec la fonction pause ; l’invite devient alors -1->, indiquant que l’on est dans le premier niveau de sous-environnement. On est également dans une telle configuration lorsque l’on interrompt l’exécution d’une fonction (par exemple avec la combinaison de touches CTRL+C). Pour revenir à l’environnement précédent, il faut utiliser la commande return.

Si l’on utilise return sans argument, les variables ne sont pas transmises à l’environnement père. Il est possible de transmettre les variables a1, a2, …, an dans l’environnement père, avec la syntaxe (x1, x2, …, xn)=return(a1, a2, …, an), où x1, x2, …, xn sont les noms des variables dans l’environnement père.

La commande clear permet de « nettoyer » un environnement, c’est-à-dire de supprimer toutes les variables.

Voir aussi

Logiciels similaires

• PsiLAB, homonyme (en prononciation anglaise) et également destiné aux calculs mathématiques, traitement des données et affichage graphique
• LiveMath
• AMESim
• MATLAB
• GNU Octave
• SAGE_(logiciel_de_calcul_formel)
• Sysquake
• FreeMat

Liens externes

• (fr) Site officiel

• (fr) Documentation

• (fr) Interview audio de Claude Gomez, directeur du consortium Scilab

Notes et références

• Portail des logiciels libres
• Portail des mathématiques