Produit extérieur

En mathématiques, la notion de produit extérieur permet de rendre compte de façon algébrique des notions de parallélogrammes, parallélépipèdes, etc... de dimensions quelconques, vus comme produits des vecteurs qui en représentent les côtés.

Parmi les obstacles à la compréhension de la notion de produit extérieur, il faut insister sur le fait que la notation (dit wedge) universellement employée pour désigner le produit extérieur, opération associative pouvant porter sur les vecteurs de tout espace vectoriel, coïncide avec celle employée en France pour désigner une opération non associative portant uniquement sur les vecteurs d'un espace euclidien orienté à trois dimension et appelée produit vectoriel. De natures différentes, ces deux opérations entretiennent des relations étroites (liées à la dualité de Hodge), d'où un risque de confusion (la situation est meilleure en anglais, le produit vectoriel, appelé "cross product", y étant le plus souvent noté ). Plus généralement, du fait de l'existence de nombreux isomorphismes plus ou moins naturels entre les objets en jeu, les domaines concernés par le calcul extérieur sont affectés d'un certain nombre de variations terminologiques et de notations selon les communautés scientifiques qui les emploient, variations qui peuvent aussi être sources de confusion.

Selon le point de vue le plus classique, le fait qu'un parallélépipède appuyé sur une famille de vecteurs soit "aplati" dès que cette famille est liée conduit à envisager le produit extérieur comme résultant d'une antisymétrisation du produit tensoriel, c'est-à-dire de la forme la plus générale de produit associatif. Une telle antisymétrisation est réalisée par un passage au quotient, en l'occurrence le quotient de l'algèbre tensorielle associée à l'espace vectoriel sur lequel on travaille par l'idéal bilatère de cette algèbre qu'y engendrent les carrés tensoriels , puisque ceux-ci sont destinés à être "aplatis". On obtient ainsi l'algèbre extérieure d'un espace vectoriel E. Ainsi, d'une certaine façon, la notion d'algèbre extérieure d'un espace vectoriel précède celle du produit extérieur de deux vecteurs.

Le produit extérieur et le produit tensoriel agissant au sein d'algèbres différentes, il n'est en principe pas possible de combiner dans une même expression des produits tensoriels et des produits extérieurs. Ainsi, la formule

parfois présentée comme une définition du produit extérieur ne doit pas être prise au pied de la lettre, mais comme exprimant la possibilité d'injecter l'espace vectoriel dans , où désigne le sous-espace vectoriel de l'algèbre extérieure engendré par les "parallélogrammes" (ou bivecteurs) . Cette injection permet en effet d'identifier à un sous-espace de , en identifiant le bivecteur au tenseur antisymétrique . Laurent Schwartz dans son ouvrage "Les tenseurs" (Hermann, 1975) indique (p. 103) qu'une telle identification est peu recommandée.

Cependant, dans le cas particulier où l'espace vectoriel E est donné comme l'espace dual F ^* d'un espace F, et s'interprètent alors naturellement comme, respectivement, algèbre des formes multilinéaires alternées et algèbre des formes multilinéaires sur F. Dans ce cas, les espaces vectoriels sont naturellement des sous-espaces des . En particulier, de ce point de vue, le produit extérieur de deux formes linéaires est la forme bilinéaire alternée définie par la formule

Dans l'algèbre extérieure , on n'a pas en général .

Le produit extérieur en algèbre géométrique

Le produit extérieur a été imaginé vers 1844 par le mathématicien Hermann Grassmann. Le concept de produit extérieur a été intégré par William Kingdon Clifford à son algèbre géométrique, appelée aussi algèbre de Clifford, laquelle généralise et développe les travaux de Grassmann ainsi que ceux de William Rowan Hamilton en 1843 sur les quaternions.

Propriétés du produit extérieur de vecteurs

Différents produits extérieurs

Contrairement au produit vectoriel de deux vecteurs, le produit extérieur de deux vecteurs n'est pas un vecteur, mais une nouvelle entité à part entière qui est nommée un bivecteur. Alors que le produit vectoriel n'est valable que dans un espace à 3 dimensions, le produit extérieur est valable pour tout espace de dimension supérieure à un.

Le produit extérieur de deux vecteurs est antisymétrique, c'est-à-dire que

Ce qui implique

Le produit extérieur de vecteurs est associatif

Le produit extérieur est bilinéaire

    (distributivité pour l'addition)

Si l'espace est pourvu d'une métrique euclidienne, alors le module du bivecteur est

C'est l'aire du parallélogramme construit sur les deux vecteurs a et b.

Multiple produit extérieur

Dans le cas général, on peut former des entités que l'on peut appeler des p-vecteurs ou hypervecteurs de grade p au moyen du produit extérieur. On a ainsi

Quand p est égal au nombre de dimensions de l'espace, on a :

     c'est-à-dire un multiple de l'unité pseudoscalaire.

Par exemple dans un espace à trois dimensions, l'entité de grade trois, donc le grade le plus élevé de l'espace, est appelé un trivecteur.

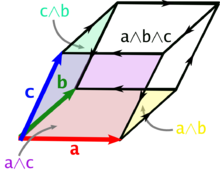
 , où le scalaire vaut le volume du parallélipipède construit sur les vecteurs.

Si le grade q du q-vecteur est strictement supérieur au nombre de dimensions de l'espace, alors on a :

Ce qui se conçoit aisément, vu que dans un espace à n dimensions il ne peut y avoir que n vecteurs linéairement indépendants. Les vecteurs supplémentaires peuvent dès lors s'exprimer comme combinaisons linéaires des autres vecteurs, ce qui rendra nul le produit.

Relation avec le produit vectoriel

Le produit extérieur et le produit vectoriel de Gibbs sont liés par une relation de dualité. Le résultat d'un produit vectoriel est en effet un bivecteur déguisé, le bivecteur étant remplacé par le vecteur qui en est le dual dans l'espace à trois dimensions. Ceci explique pourquoi le produit vectoriel n'est valable que dans espace à trois dimensions. C'est, en effet, uniquement dans un tel espace que le dual d'un bivecteur est un vecteur.

On peut passer d'un produit vectoriel à un produit extérieur au moyen de la relation suivante :

   où I est l'unité pseudoscalaire de l'espace à 3 dimensions. Ici la croix symbolise le produit vectoriel.

Produit extérieur de multivecteurs

Le produit extérieur est aussi valable pour les multivecteurs. Par multivecteur on entend l'élément le plus général de l'algèbre géométrique, à savoir, pour un espace à n dimensions :

M = α + βA₁ + γA₂ + ... + μA_k + ...νA_n

où les lettres grecques représentent des valeurs scalaires et les A indicés des p-vecteurs avec p < = n

Voir aussi

• Tenseur

v · d · m Opérations binaires
Numériques En ensemble ordonné Structurelles Autres Élémentaires + Addition − Soustraction Multiplication Division Puissance Arithmétiques div Quotient euclidien mod Reste euclidien pgcd PGCD ppcm PPCM Combinatoires () Coefficient binomial A Arrangement Ensembles de parties Union Complémentation Intersection Δ Différence symétrique Ordre total min  Minimum max  Maximum Treillis Borne inférieure Borne supérieure Ensembles Produit cartésien Somme disjointe Puissance ensembliste Groupes Somme directe Produit libre Produit en couronne Modules Produit tensoriel Hom Homomorphisme Tor Torsion Ext Extension Arbres Enracinement Variétés connexes Somme connexe Espaces pointés Bouquet Smash produit Joint Fonctionnelles Composition de fonctions Produit de convolution Vectorielles Produit scalaire Produit vectoriel Produit vectoriel généralisé Algébriques [,] Crochet de Lie {,} Crochet de Poisson Produit extérieur Homologiques Cup produit Produit d'intersection Séquentielles + Concaténation
Logique booléenne : ET (conjonction) • OU (disjonction) • OU exclusif • IMP (implication) • EQV (équivalence)

• Portail des mathématiques