Moment Angulaire

Moment Angulaire: Moment angulaire

Pour les articles homonymes, voir Moment.

Un gyroscope tournant sur un clou

En physique, le moment angulaire ou moment cinétique est la grandeur physique qui joue un rôle analogue à la quantité de mouvement dans le cas des rotations. Comme le moment angulaire dépend du choix de l'origine (ainsi que du référentiel d'étude (R)) il faut toujours spécifier cette origine et ne jamais combiner des moments angulaires ayant des origines différentes.

Sommaire

1 Cas d'un point matériel

1.1 Définition

1.2 Théorème du moment cinétique pour un point matériel

2 Exemples d'application

2.1 Mouvement à force centrale : cas général

2.2 Mouvement à force centrale : cas où la force dérive d'une énergie potentielle

2.3 Quelques remarques et références additionnelles

3 Cas d'un système matériel

3.1 Définition dans le cas général

3.2 Thèorème de Koenig pour le moment cinétique

3.3 Cas d'un solide: tenseur d'inertie

4 Voir aussi

4.1 Articles connexes

4.2 Liens externes

Cas d'un point matériel

On appelle point matériel ou corps ponctuel un système mécanique dont les dimensions sont petites devant les distances caractéristiques du mouvement étudié (distance parcourue, rayon d'une orbite...). Le système mécanique est alors modélisé par un point géométrique M auquel est associé sa masse m.

Définition

Pour un point matériel M de vecteur position 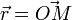$\vec{r}=\vec{OM}$ le moment cinétique ou angulaire 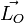$\vec{L_{O}}$ par rapport à l'origine O est défini par :
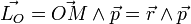$\vec{L_{O}}=\vec{OM} \wedge \vec{p}=\vec{r}\wedge \vec{p}$ , (1)
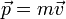où $\vec{p}=m\vec{v}$ est la quantité de mouvement de la particule. Le moment cinétique est donc le moment de cette dernière par rapport à O. $\wedge$ est l'opérateur produit vectoriel.

Un exemple simple est celui d'une particule décrivant un cercle de centre O et de rayon r : 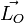$\vec{L_{O}}$ est dirigé selon l'axe du disque et vaut 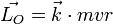$\vec{L_{O}} = \vec{k} \cdot mvr$ . Le sens 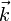$\vec{k}$ du vecteur moment cinétique ne recouvre pas d'une réalité physique mais d'une convention, c'est un vecteur axial.

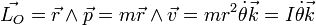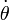Par analogie avec la quantité de mouvement, le moment cinétique permet de définir l'analogue de la masse : le moment d'inertie $I$ . En effet : $\vec{L_{O}}=\vec{r}\wedge \vec{p}=m \vec{r}\wedge \vec{v}= mr^{2}\dot{\theta} \vec{k} = I \dot{\theta} \vec{k}$ , où $\dot{\theta}$ est la vitesse angulaire du point M, à laquelle on peut faire correspondre le vecteur axial 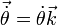$\vec{{\dot{\theta}}}=\dot{\theta} \vec{k}$ . Le moment cinétique s'écrit finalement :
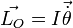$\vec{L_{O}}= I \vec{\dot{\theta}}$ .
Théorème du moment cinétique pour un point matériel

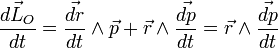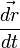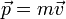Si l'on dérive membre à membre la définition (1) du moment angulaire, il vient, en supposant O fixe dans (R): $\frac{\vec{dL_{O}}}{dt}=\frac{\vec{dr}}{dt}\wedge \vec{p}+\vec{r}\wedge \frac{\vec{dp}}{dt}=\vec{r}\wedge \frac{\vec{dp}}{dt}$ , puisque $\frac{\vec{dr}}{dt}$ et $\vec{p}=m\vec{v}$ sont colinéaires.

Par ailleurs pour un corps ponctuel, on a (relation fondamentale de la dynamique):

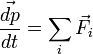$\frac{\vec{dp}}{dt}=\sum_{i} \vec{F_{i}}$ , (2), le terme de droite correspondant à la somme des forces 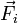$\vec{F_{i}}$ (réelles ou "d'inertie") exercées sur le corps.

Par suite il vient l'équation suivante, dite théorème du moment cinétique:
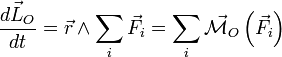$\frac{\vec{dL_{O}}}{dt}=\vec{r}\wedge \sum_{i} \vec{F_{i}}=\sum_{i} \vec{\mathcal{M}_{O}}\left (\vec{F_{i}}\right)$ , (3)
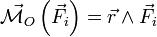où $\vec{\mathcal{M}_{O}}\left ( \vec{F_{i}}\right)= \vec{r}\wedge \vec{F_{i}}$ est le moment de la force 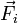$\vec{F_{i}}$ par rapport au point O.

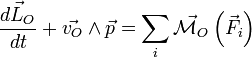Remarque: par rapport à un point O mobile dans (R), le théorème du moment cinétique s'écrit: $\frac{\vec{dL_{O}}}{dt}+\vec{v_{O}}\wedge \vec{p}=\sum_{i} \vec{\mathcal{M}_{O}}\left (\vec{F_{i}}\right)$ .
La seule différence vient de l'addition d'un terme complémentaire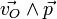 $\vec{v_{O}}\wedge \vec{p}$ dans le membre de gauche de la relation (3).

Exemples d'application

Mouvement à force centrale : cas général

Un cas particulier très important d'utilisation du moment cinétique est celui du mouvement à force centrale, où le point matériel M est soumis à une seule force 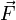$\vec{F}$ dont la direction passe par un point fixe dans (R), appelé centre de force. 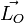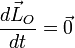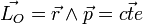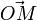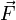Par suite en prenant ce centre de force pour origine O, le théorème du moment cinétique (3) implique que le moment cinétique $\vec{L_{O}}$ est une intégrale première du mouvement : $\frac{\vec{dL_{O}}}{dt}=\vec{0}$ , soit $\vec{L_{O}}=\vec{r}\wedge \vec{p}=\vec{cte}$ , puisque $\vec{OM}$ et $\vec{F}$ sont colinéaires.

Par conséquent le vecteur position 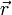$\vec{r}$ et la quantité de mouvement 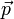$\vec{p}$ du corps sont à tout instant perpendiculaires à un vecteur de direction constante : la trajectoire est donc plane, entièrement contenue dans le plan perpendiculaire à 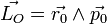$\vec{L_{O}}=\vec{r_{0}}\wedge \vec{p_{0}}$ (l'indice "0" désigne les valeurs initiales des grandeurs).

Le mouvement ne comportant que deux degrés de liberté on se place en coordonnées polaires (r,θ) dans le plan de la trajectoire. Il vient ainsi :

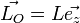$\vec{L_{O}}=L\vec{e_{z}}$ , avec 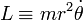$L\equiv mr^{2}\dot{\theta}$ constante.

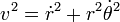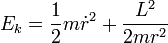Compte tenu de $v^{2}=\dot{r}^{2}+r^{2}\dot{\theta}^{2}$ en coordonnées polaires, l'énergie cinétique du point matériel peut se séparer en une partie radiale et une partie angulaire. Elle s'écrit alors $E_{k}=\frac{1}{2}m\dot{r}^{2}+\frac{L^{2}}{2mr^{2}}$ .

Mouvement à force centrale : cas où la force dérive d'une énergie potentielle

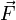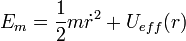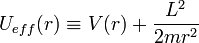Si la force centrale $\vec{F}$ dérive d'une énergie potentielle $V (r)$ , l'énergie mécanique du corps se met sous la forme: $E_{m}=\frac{1}{2}m\dot{r}^{2}+U_{eff}(r)$ avec $U_{eff}(r)\equiv V(r)+\frac{L^{2}}{2mr^{2}}$ , énergie potentielle effective.

On se ramène à un mouvement unidimensionnel d'une particule fictive dans un potentiel $U e f f (r)$ . Le terme 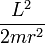$\frac{L^{2}}{2mr^{2}}$ étant positif et croissant à courte distance, il joue le rôle de "barrière de potentiel centrifuge".

Quelques remarques et références additionnelles

De nombreux auteurs supposent qu'une force centrale dérive toujours d'une énergie potentielle: ceci est faux en général. Par exemple, pour le pendule simple, la force de tension du fil est une force centrale car elle passe toujours par le point de fixation O du pendule, MAIS elle ne dérive pas d'une énergie potentielle.

Une application importante des développements précédents est dans l'étude du mouvement keplerien des planètes et des satellites. Les trajectoires sont alors des courbes fermées: ellipses.

Il convient de souligner qu'en général les trajectoires obtenues pour une énergie potentielle V(r) quelconque ne sont pas des courbes fermées: seuls le potentiel coulombien attractif 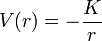$V(r)=-\frac{K}{r}$ (K constante) et le potentiel harmonique $V (r) = α r 2$ en donneront. Cela provient de l'existence, pour ces potentiels, d'une intégrale première additionnelle (pour le potentiel coulombien, il s'agit du vecteur de Runge-Lenz), associé à une symétrie supplémentaire (par transformation du groupe O(4)).

Cas d'un système matériel

Définition dans le cas général

Si un système est constitué de plusieurs particules (modèle discret), le moment angulaire total est obtenu en additionant ou intégrant le moment angulaire de chacun de ses constituants. Il est également possible de se placer dans la limite des milieux continus pour décrire certains systèmes mécaniques (solides, notamment).

Suivant que l'on adopte un modèle discret ou continu, le moment cinétique du système (S) par rapport à un point O s'écrit :

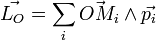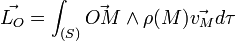
$\vec{L_{O}}=\sum_{i} \vec{OM_{i}}\wedge \vec{p_{i}}$ ou $\vec{L_{O}}=\int_{(S)} \vec{OM}\wedge \rho (M)\vec{v_{M}}d\tau$

Ces expressions générales ne sont guère utilisables directement. Le théorème de Koenig relatif au moment cinétique permet d'en donner une forme plus compréhensible physiquement.

Dans le cas d'un système à 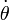$\dot{\theta}$ constante (cas des solides notamment), on peut aussi écrire :

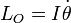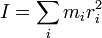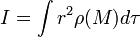$L_{O}= I \dot{\theta}$ où $I=\sum_{i} m_{i}r_{i}^2$ ou $I=\int r^2\rho (M) d\tau$ .

Thèorème de Koenig pour le moment cinétique

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Cas d'un solide: tenseur d'inertie

Voir aussi

Articles connexes

Moment (mécanique)

Moment cinétique quantique

Moment cinétique orbital et spin en mécanique quantique

Moment d'inertie

Pseudovecteur

Liens externes

Une vidéo explicative sur la conservation du moment cinétique

Portail de la physique

Ce document provient de « Moment angulaire ».

Catégories : Grandeur physique | Mécanique classique | Physique quantique

Contenu soumis à la licence CC-BY-SA. Source : Article Moment Angulaire de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Moment angulaire — ● Moment angulaire synonyme de moment cinétique … Encyclopédie Universelle
Moment angulaire — Pour les articles homonymes, voir Moment. Un gyroscope tournant sur un clou En physique, le moment angulaire ou moment cinétique est la grandeur physique qui joue dans le ca … Wikipédia en Français
moment angulaire — judesio kiekio momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus dalelės padėties vektoriaus iš tam tikro taško į dalelę ir jos judesio kiekio vektorinei sandaugai, t. y. L = r · p; čia L – judesio kiekio momento… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
moment angulaire — judesio kiekio momentas statusas T sritis Standartizacija ir metrologija apibrėžtis Materialiojo taško arba dalelės spindulio vektoriaus ir judesio kiekio vektorinė sandauga. Dažniausiai apibūdina sukamąjį judesį taško arba ašies, iš kurios yra… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
moment angulaire — sukimo impulsas statusas T sritis fizika atitikmenys: angl. angular impulse; impulsive moment vok. Drehimpuls, m rus. вращательный импульс, m; момент импульса, m pranc. impulsion angulaire, f; moment angulaire, m; moment cinétique, m … Fizikos terminų žodynas
moment angulaire — judesio kiekio momentas statusas T sritis fizika atitikmenys: angl. angular moment; moment of momentum; rotation moment vok. Drehimpuls, m; Impulsmoment, n; Rotationsmoment, n rus. момент импульса, m; момент количества движения, m; угловой момент … Fizikos terminų žodynas
moment angulaire total — pilnutinis judesio kiekio momentas statusas T sritis fizika atitikmenys: angl. total angular moment vok. Gesamtdrehimpuls, m rus. полный момент количества движения, m pranc. moment angulaire total, m; moment cinétique total, m … Fizikos terminų žodynas
moment angulaire quadridimensionnel — keturmatis judesio kiekio momentas statusas T sritis fizika atitikmenys: angl. four angular momentum; four dimensional angular momentum vok. vierdimensionaler Drehimpuls, m; Vierdrehimpuls, m rus. четырёхмерный момент количества движения, m pranc … Fizikos terminų žodynas
conservation du moment angulaire — judesio kiekio momento tvermė statusas T sritis fizika atitikmenys: angl. conservation of angular momentum; conservation of moment of momentum vok. Drehimpulserhaltung, f; Erhaltung des Drehimpulses, f rus. сохранение момента количества движения … Fizikos terminų žodynas
vecteur moment angulaire — judesio kiekio momento vektorius statusas T sritis fizika atitikmenys: angl. angular momentum vector vok. Drehimpulsvektor, m; Impulsmomentvektor, m rus. вектор момента импульса, m; вектор момента количества движения, m; вектор углового момента,… … Fizikos terminų žodynas

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts