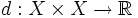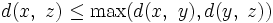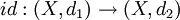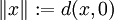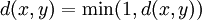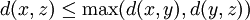- Metrique (mathematiques)
-
Métrique (mathématiques)
 Pour les articles homonymes, voir Métrique.
Pour les articles homonymes, voir Métrique.En mathématiques, une métrique ou fonction distance est une fonction qui définit une distance entre les éléments d'un ensemble. Un ensemble avec une métrique est appelé un espace métrique. Une métrique induit une topologie sur un ensemble mais toutes les topologies ne sont pas engendrées par une métrique. Lorqu'une topologie peut être décrite par une métrique, nous l'appelons espace métrisable.
En géométrie différentielle, le mot "métrique" est aussi utilisé pour faire référence à une structure définie seulement sur un espace vectoriel qui est plus proprement qualifié un tenseur métrique (ou riemannien ou métrique pseudo-riemannienne).
Sommaire
Définition
Une métrique sur un ensemble X est une fonction (appelée la fonction distance ou simplement distance)
(où
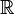 est l'ensemble des nombres réels). Pour tout x, y, z dans X, cette fonction doit satisfaire les conditions suivantes :
est l'ensemble des nombres réels). Pour tout x, y, z dans X, cette fonction doit satisfaire les conditions suivantes :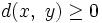 (non-négativité)
(non-négativité)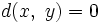 si et seulement si
si et seulement si 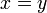 (identité des indiscernables)
(identité des indiscernables)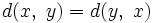 (symétrie)
(symétrie)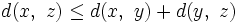 (inégalité triangulaire).
(inégalité triangulaire).
Une métrique d sur X est appelée intrinsèque si deux points quelconques x et y dans X peuvent être joints par une courbe de longueur arbitrairement proche de d(x, y).
Pour les ensembles où une addition
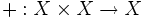 est définie, nous appelons d une métrique invariante par translation si
est définie, nous appelons d une métrique invariante par translation si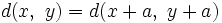 quels que soient x,y et a dans X.
quels que soient x,y et a dans X.
Si l'inégalité triangulaire est renforcée par
la métrique est appelée ultramétrique, voir ci-dessous.
Notes
Ces conditions expriment les notions intuitives du concept de distance. Par exemple, que la distance entre des points distincts est strictement positive et que la distance de x vers y est la même que la distance de y vers x. L'inégalité triangulaire signifie que la distance parcourue directement entre x et z, n'est pas plus grande que la distance à parcourir en partant d'abord de x vers y puis de y vers z. Euclide dans ses travaux démontra que la plus courte distance entre deux points est une droite; ce qui était l'inégalité triangulaire pour sa géométrie.
La propriété 1 (d(x, y) ≥ 0) découle des propriétés 2 et 4 et ne constitue donc pas un axiome indépendant.
Exemples
- La métrique discrète : si x = y alors
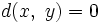 . Autrement,
. Autrement, 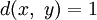 .
. - La métrique euclidienne est un invariant par translation.
- Plus généralement, toute métrique induite par une norme (voir ci-dessous) est un invariant par translation.
- Si
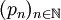 est une suite de seminormes définissant un espace vectoriel topologique (localement convexe) E, alors
est une suite de seminormes définissant un espace vectoriel topologique (localement convexe) E, alors
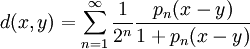
- est une métrique définissant la même topologie. (On peut remplacer
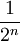 par n'importe quelle suite sommable (an) de nombres strictement positifs.)
par n'importe quelle suite sommable (an) de nombres strictement positifs.)
Équivalence de métriques
Pour un ensemble donné X, deux métriques
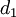 et
et 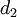 sont appelées topologiquement équivalentes (uniformément équivalentes) si l'application identité
sont appelées topologiquement équivalentes (uniformément équivalentes) si l'application identitéest un homéomorphisme (isomorphisme uniforme).
Relation de normes et métriques
Étant donné un espace vectoriel normé
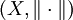 nous pouvons définir une métrique sur X par
nous pouvons définir une métrique sur X par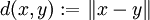 .
.
La métrique d est dite "induite par" la norme
 .
.Inversement, si une métrique d sur un espace vectoriel X satisfait les propriétés
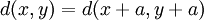 (invariance par translation)
(invariance par translation)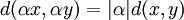 (homogénéité)
(homogénéité)
alors, nous pouvons définir une norme sur X par
De manière similaire, une seminorme induit une pseudométrique et une pseudométrique invariante par translation homogène induit une seminorme.
Concepts reliés et systèmes axiomatiques alternatifs
Certains auteurs utilisent la droite réelle achevée et permettent à la fonction distance d d'atteindre la valeur
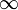 . Une telle métrique est appelée une métrique étendue. Chaque métrique étendue peut être rmeplacée vers une métrique finie en utilisant :
. Une telle métrique est appelée une métrique étendue. Chaque métrique étendue peut être rmeplacée vers une métrique finie en utilisant :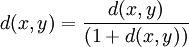 ou
ou
et les deux concepts d'espace métrique sont par conséquent équivalents jusqu'aux notions de topologie (telles que la continuité ou la convergence) concernées.
Une métrique est appelée une ultramétrique si elle satisfait à la version plus forte de l'inégalité triangulaire :
- Quels que soient x, y, z dans M,
Si la propriété 2 est enlevée, on obtient les espaces pseudométriques. En enlevant la propriété 3 à la place, on obtient les espaces quasimétriques. Néanmoins, en perdant la symétrie dans ce cas, on change habituellement la propriété 2 tel que les deux
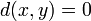 et
et 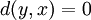 sont nécessaires pour que x et y soient identifiés. En enlevant la propriété 4, on obtient les espaces semimétriques. Toutes les combinaisons ci-dessus sont possibles et sont identifiées par les noms correspondants (tel que quasi-pseudo-ultramétrique).
sont nécessaires pour que x et y soient identifiés. En enlevant la propriété 4, on obtient les espaces semimétriques. Toutes les combinaisons ci-dessus sont possibles et sont identifiées par les noms correspondants (tel que quasi-pseudo-ultramétrique).À partir du point de vue de la théorie des catégories, la pseudométrique étendue et les espaces pseudométriques étendus, avec leurs applications correspondantes non développables, sont les catégories d'espace métrique qui se comportent le mieux. On peut prendre des produits et des coproduits arbitraires et former des objets quotient avec une catégorie donnée. Si on enlève "étendu", on peut seulement prendre des produits et des coproduits finis. Si on enlève "pseudo", on ne peut plus prendre des quotients. Les espaces d'approche sont une génaralisation des espaces métriques qui maintiennent ces bonnes propriétés de catégorie.
La requête que la métrique prenne des valeurs dans
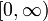 peut être aussi assouplie en considérant les métriques avec des valeurs dans d'autres espaces orientés. La reformulation des axiomes dans ce cas conduit à la construction des espaces uniformes : des espaces topologiques avec une structure abstraite permettant de comparer les topologies locales de points différents.
peut être aussi assouplie en considérant les métriques avec des valeurs dans d'autres espaces orientés. La reformulation des axiomes dans ce cas conduit à la construction des espaces uniformes : des espaces topologiques avec une structure abstraite permettant de comparer les topologies locales de points différents.En géométrie différentielle, on considére les tenseurs métriques, qui peuvent être pensés comme des fonctions métriques "infinitésimales", et sont définis comme des produits internes sur l'espace tangent avec une exigence de dérivabilité appropriée. Alors qu'il n'y a pas de fonctions métriques définies dans cet article, ils induisent des fonctions métriques par intégration. Une variété avec un tenseur métrique est appelé une variété riemannienne. Si on enlève l'exigence de définition positive des espaces de produit interne, alors on obtient un tenseur métrique pseudo-riemannien, qui s'intègre en une pseudométrique. Ceux-ci sont utilisés dans l'étude géométrique de la théorie de la relativité, ou le tenseur est aussi appelé l'"invariant de distance".
Voir aussi
- Portail des mathématiques
Catégorie : Espace métrique
Wikimedia Foundation. 2010.