Optimisation (mathématiques)

L'optimisation est une branche des mathématiques, cherchant à analyser et à résoudre analytiquement ou numériquement les problèmes qui consistent à déterminer le meilleur élément d'un ensemble, au sens d'un critère quantitatif donné. Ce mot vient du latin optimum qui signifie le meilleur.

L’optimisation joue un rôle important en recherche opérationnelle (donc en économie et microéconomie), dans les mathématiques appliquées (fondamentales pour l'industrie et l'ingénierie), en analyse et en analyse numérique, en statistique pour l’estimation du maximum de vraisemblance d’une distribution, pour la recherche de stratégies dans le cadre de la théorie des jeux, ou encore en théorie du contrôle et de la commande.

Aujourd'hui, tous les systèmes susceptibles d’être décrits par un modèle mathématique sont optimisés. La qualité des résultats et des prédictions dépend de la pertinence du modèle, de l’efficacité de l’algorithme et des moyens pour le traitement numérique.

Domaines d’application

Ils sont extrêmement variés : optimisation d’un trajet, de la forme d’un objet, d’un prix de vente, d’une réaction chimique, du contrôle aérien, du rendement d’un appareil, du fonctionnement d'un moteur, de la gestion des lignes ferroviaires, du choix des investissements économiques, de la construction d’un navire, etc. L’optimisation de ces systèmes permet de trouver une configuration idéale, d’obtenir un gain d’effort, de temps, d’argent, d’énergie, de matière première, ou encore de satisfaction.

Très loin de constituer une liste exhaustive, ces quelques exemples attestent de la variété des formulations et préfigure la diversité des outils mathématiques susceptibles de résoudre ces problèmes.

Définition

Plus formellement, l'optimisation est l’étude des problèmes qui sont de la forme :

Étant donné : une fonction $f : A \rightarrow \mathbb R$ d’un ensemble $\displaystyle A$ dans l'ensemble des nombre réels

Rechercher : un élément $\displaystyle x_0$ de $\displaystyle A$ tel que $f(x_0) \geqslant f(x)$ pour tous les $\displaystyle x$ en $\displaystyle A$ (« maximisation ») ou tel que $f(x_0) \leqslant f(x)$ pour tous les $\displaystyle x$ en $\displaystyle A$ (« minimisation »).

Les éléments de $\displaystyle A$ sont appelés les solutions admissibles, la fonction $\displaystyle f$ est la fonction objectif et $\displaystyle x_0$ est la (une) solution optimale.

Puisque la minimisation de $\displaystyle f$ est équivalente à la maximisation de $\displaystyle -f$ , une méthode pour trouver le minimum (ou le maximum) suffit à résoudre le problème d'optimisation.

Le plus souvent, $\displaystyle A$ est un sous-ensemble de l’espace euclidien $\mathbb R^n$ . Lorsqu’il est constitué des vecteurs dont les coordonnées satisfont un certain nombre de contraintes (de type égalité ou inégalité). On parle d'optimisation combinatoire lorsque $\displaystyle A$ est un sous-ensemble de $\mathbb N^n$ ou de $\mathbb N^p\times \mathbb R^q$ .

Extrema locaux : un maximum local $\displaystyle x^*$ est défini comme un point de $\displaystyle A$ pour lequel il existe un voisinage $\displaystyle V$ de $\displaystyle x^*$ tel que pour tout $x\in V \cap A$ , $f(x) \leqslant f(x^*)$ ; dans ce voisinage de $\displaystyle x^*$ , les valeurs de la fonction dominent la valeur en ce point. Lorsque $\displaystyle A$ est un sous-ensemble de $\mathbb R^n$ , ou plus généralement d’un espace vectoriel normé, la définition est équivalente à l’existence d’un $\displaystyle \delta > 0$ tel que, pour tout $x\in A$ satisfaisant $||x - x^*|| \leqslant \delta$ , on a $f(x) \leqslant f(x^*)$ . Un minimum local est défini semblablement.

Il est en général facile de déterminer numériquement des maxima locaux (ils peuvent être nombreux). Pour vérifier que la solution trouvée est un maximum global, il est parfois possible de recourir à des connaissances additionnelles sur le problème. Selon la nature de $A$ et/ou de la fonction $f$ , divers théorèmes (principe du maximum) assurent des propriétés particulières de la solution optimale qui simplifient sa recherche.

Notation

Les problèmes d’optimisation sont souvent exprimés avec une notation spéciale. Voici quelques exemples :

$\min_{x \in \mathbb{R}} x^2 + 1$

On cherche la valeur minimale pour l’expression $\displaystyle x^2 + 1$ , où $\displaystyle x$ s’étend sur les nombres réels $\mathbb R$ . La valeur minimale dans ce cas est 1, s’occasionnant à $\displaystyle x = 0$ .

$\max_{x \in \mathbb{R}} 2x$

On cherche la valeur maximale pour l’expression $\displaystyle 2x$ , où $x$ s’étend sur les réels. Dans ce cas, il n’y a pas de tel maximum puisque l’expression n’est pas bornée, donc la réponse est « l’infini » ou « indéfini ».

$\arg \min_{x \in ]-\infty, -1]} x^2 + 1$

On cherche la ou les valeurs de $\displaystyle x$ dans l'intervalle $]-\infty, -1]$ qui minimise l'expression $\displaystyle x^2 + 1$ (la valeur minimale véritable de cette expression n'est pas importante). Dans ce cas, la réponse est $\displaystyle x = -1$ .

$\arg \max_{x \in [-5, 5], y \in \mathbb{R}} x \cos(y)$

On cherche la ou les paires $\displaystyle (x, y)$ qui maximisent la valeur de l'expression $\displaystyle x \cos(y)$ , avec la contrainte ajoutée que la valeur absolue de $\displaystyle x$ ne peut excéder 5 (à nouveau, la valeur maximale véritable de l'expression n'est pas importante). Dans ce cas, les solutions sont les paires de la forme $\displaystyle (5, 2k\pi)$ et $\displaystyle (-5, (2k + 1)\pi)$ , où $\displaystyle k$ s'étend sur tous les entiers.

Quelques classes de problèmes

L'optimisation linéaire étudie le cas où la fonction objectif et les contraintes caractérisant l’ensemble $A$ sont linéaires. C’est une méthode très employée pour établir les programmes des raffineries pétrolières, mais aussi pour déterminer la composition la plus rentable d’un mélange salé, sous contraintes, à partir des prix de marché du moment.
L'optimisation linéaire en nombres entiers étudie les problèmes d'optimisation linéaire dans lesquels certaines ou toutes les variables sont contraintes de prendre des valeurs entières. Ces problèmes peuvent être résolus par différentes méthodes : séparation et évaluation, méthode des plans sécants.
L'optimisation quadratique étudie le cas où la fonction objectif est une forme quadratique (avec contraintes linéaires pour $A$ )
L'optimisation non linéaire étudie le cas général dans lequel l’objectif ou les contraintes (ou les deux) contiennent des parties non linéaires, éventuellement non-convexes.
L'optimisation stochastique (en) étudie le cas dans lequel certaines des contraintes dépendent de variables aléatoires. En optimisation robuste, les aléas sont supposés être situés dans des intervalles autour de positions nominales et on cherche à optimiser le système soumis à de tels aléas, dans le pire des cas.
La programmation dynamique utilise la propriété qu’une solution optimale se compose nécessairement de sous-solutions optimales (attention : le contraire n'est pas vrai en général) pour décomposer le problème en évitant l’explosion combinatoire. Elle est utilisable lorsque la fonction objectif est une somme de fonctions monotones croissantes dont les arguments sont des inconnues distinctes. C’est la programmation dynamique qui permet par exemple
- aux avionneurs de trouver les plans de décollage optimaux de leurs engins,
- aux ingénieurs de bassin de répartir la production minière entre leurs différents puits,
- aux producteurs d’électricité de planifier la marche des usines hydroélectriques,
- aux media planners de répartir efficacement un budget de publicité entre différents supports.

Méthodes numériques

Une technique de résolution d’un problème d’optimisation mathématique désigne ici

la transformation du problème d’origine en un problème équivalent,
une méthode théorique dont la description permet l’élaboration d’un algorithme numériquement applicable.

Le choix d’une technique appropriée dépend de

la nature de la fonction objectif $f$ , de sa régularité (continuité, dérivabilité), de propriétés spécifiques (parité, convexité), de la connaissance de voisinages de ses extrema,
des contraintes caractérisant l'ensemble $A$ des solutions admissibles.

Simplifications

Le problème d’origine est remplacé par un problème équivalent. Par exemple un changement de variables permettant de décomposer le problème en sous-problèmes ou la substitution d’inconnues permettant d’en réduire le nombre.

La technique du multiplicateur de Lagrange permet de s’affranchir de certaines contraintes (de type égalité) ; cette méthode revient en effet à introduire des pénalités croissantes à mesure que la solution se rapproche des contraintes. Un algorithme dû à Hugh Everett permet de mettre à jour de façon cohérente les valeurs des multiplicateurs à chaque itération pour garantir la convergence. Celui-ci a également généralisé l'interprétation de ces multiplicateurs pour les appliquer à des fonctions qui ne sont ni continues, ni dérivables. Le lambda exprime un coefficient de pénalité (notion de coût marginal d’une contrainte en économie).

Recherche des zéros du gradient

De nombreuses méthodes et algorithmes permettent de trouver un zéro de la dérivée de $f$ (certains sont spécifiques aux fonctions d’une variable) ou de son gradient $\mathbf{\nabla} f$ . Elles s’appliquent valablement dans des situations où les contraintes sur $A$ restent peu actives.

Toutes ces méthodes se développent dans le cadre d’un procédé itératif.

Ces approches peuvent souffrir de quelques défauts :

La fonction doit être assez régulière (au moins localement) pour être dérivable (ou encore deux fois dérivable pour accéder à la matrice hessienne ou une approximation de celle-ci).
Il n’est pas toujours possible d’exprimer explicitement le gradient de la fonction objectif.
Des conditions de départ doivent être fixées avant d’amorcer le processus itératif. Le choix initial peut considérablement influencer le résultat (divergence du procédé itératif). Les méthodes à convergence rapide sont en général plus sensibles de ce point de vue.
Dans certains cas, la vitesse de convergence peut se révéler désastreuse : les itérations successives cheminent laborieusement (stagnation) le long d’une vallée étroite (fonction de Rosenbrock).
Si la solution obtenue est bien un extremum (après vérification qu’il ne s’agisse pas d’un point selle), celui-ci peut s’avérer être local.

Cas particulier : Lorsque $f$ est polynomiale de degré 2 dans ses arguments (forme quadratique et linéaire) et sans contrainte, annuler le gradient revient à résoudre un système linéaire (cf Catégorie:Analyse numérique matricielle).

Méthodes analytiques directes

Dans cette catégorie, la plupart des algorithmes généraux s’appliquent aux situations où les contraintes sur $A$ restent peu actives. Ils se basent sur quelques idées dominantes :

Déplacements le long d’une ligne portée par un gradient.
Approximation de $f$ par une fonction plus simple (par exemple le développement de Taylor d’ordre 2), mise à jour au cours des itérations.

Divers perfectionnements ont été apportés afin d’éviter :

les stagnations (par exemple méthode du gradient conjugué en optimisation non linéaire (en))
le calcul explicite ou trop fréquent de la matrice hessienne (par exemple BFGS)

Les mêmes défauts que ceux mentionnés dans la catégorie précédente peuvent aussi se présenter ici.

La Catégorie:Algorithme d'optimisation présente une liste et donne accès à ces méthodes.

Techniques de l’optimisation combinatoire

Ces techniques concernent des problèmes où une partie (au moins) des variables de l’ensemble $A$ prennent des valeurs discrètes. On les rencontre dans le cadre de

la théorie des graphes (chemin optimal dont le problème du voyageur de commerce)
la théorie des jeux (stratégies performantes)
la théorie du contrôle, de la régulation et de l’automatique (cf Catégorie:Automatique)
l’optimisation multidisciplinaire

Heuristiques et métaheuristiques

Pour résoudre des problèmes difficiles (par exemple ceux qui présentent de nombreux extrema locaux pauvres), des techniques ont été conçues pour déterminer des solutions qui ne sont pas rigoureusement optimales, mais qui s’en approchent. Ces méthodes se basent généralement sur des phénomènes physiques, biologiques, socio-psychologiques ou font appel au hasard. Les domaines d’application sont vastes et s’étendent souvent bien au-delà des problèmes pour lesquels elles ont été initialement conçues.

le recuit simulé
la méthode de Nelder-Mead avec recuit simulé
les algorithmes de colonies de fourmis
les algorithmes génétiques
les algorithmes évolutionnistes
les méthodes d’optimisation par essaims particulaires

La Catégorie:Métaheuristique présente une liste et donne accès à ces méthodes.

Techniques de l’optimisation multiobjectif

Ces problèmes sortent du cadre strict de la définition donnée plus haut : à une solution admissible de $A$ , la fonction objectif n’associe pas une valeur numérique, mais un point d’un ensemble qui sera le plus souvent associé à un vecteur. L'objectif est alors d'optimiser simultanément l'ensemble des composantes de ce vecteur. On peut aussi voir l’optimisation multiobjectif comme un ensemble de problèmes d'optimisation portant sur les mêmes paramètres, ayant des objectifs éventuellement contradictoires, et que l'on cherche à résoudre au mieux.

En général, l'espace dans lequel est exprimé le vecteur solution est muni d’un ordre partiel faisant intervenir des critères de dominance (par exemple en rapport avec la frontière de Paréto). La résolution consiste à trouver une solution dont l’objectif n’est dominé par aucun autre.

Utilisations

Les problèmes de la dynamique des corps rigides (en) (surtout la dynamique des corps rigides articulés) ont souvent besoin de techniques d'optimisation mathématique, puisqu'on peut voir la dynamique des corps rigides comme résolution d'une équation différentielle ordinaire sur une variété contrainte ; les contraintes sont diverses contraintes géométriques non linéaires telles que « ces deux points doivent toujours coïncider », ou « ce point doit toujours être sur cette courbe ». Aussi, le problème de calculer les forces de contact peut être achevé en résolvant un problème de complémentarité linéaire (en), qui peut aussi être vu comme un problème d'optimisation quadratique.

Plusieurs problèmes de conception peuvent aussi être exprimés sous forme de problèmes d’optimisation. Cette application est appelée l’optimisation de forme. Un sous-ensemble récent et croissant de ce domaine s’appelle l’Optimisation multidisciplinaire qui, bien qu’utile en plusieurs problèmes, a été particulièrement appliquée aux problèmes d'ingénierie et technologie spatiale.

Un autre domaine qui utilise les techniques d’optimisation est la recherche opérationnelle.

L’optimisation est un des outils centraux de la microéconomie qui est basée sur le principe de la rationalité et de l’optimisation des comportements, le profit pour les entreprises, et l’utilité pour les consommateurs.

En mécanique on distingue trois formes d'optimisation^[1] :

l'optimisation de taille ou optimisation paramétrique, qui consiste à optimiser des dimensions (longueur, épaisseur, diamètre, ...) de la structure mécanique ;
l'optimisation de forme (en), qui consiste à optimiser l'enveloppe d'une pièce sans changer la topologie, c'est-à-dire sans ajouter de trous dans la pièce ;
l'optimisation topologique, qui consiste à faire varier la répartition de matière au sein d'un volume de départ donné.

Historique

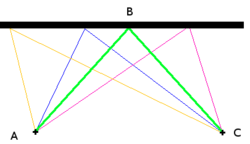
Les premiers problèmes d'optimisation auraient été formulés par Euclide, au IIIe siècle avant notre ère, dans son ouvrage historique Éléments. Trois cent ans plus tard, Héron d'Alexandrie dans Catoptrica énonce le principe du plus court chemin dans le contexte de l'optique^[2]. (voir figure)

Le plus court chemin pour aller de A à C en passant par un point B de la droite est obtenu lorsque l'angle d'incidence est égal à l'angle réfléchi (sur la figure, il s'agit du chemin vert).

Au XIIe siècle, l'apparition du calcul différentiel entraîne l'invention de techniques d'optimisation, ou du moins en fait ressentir la nécessité. Newton met au point une méthode itérative permettant de trouver les extrémums locaux d'une fonction en faisant intervenir la notion de dérivée, issue de ses travaux avec Leibniz^[3]. Cette nouvelle notion permet de grandes avancées dans l'optimisation de fonctions car le problème est ramené à la recherche des racines de la dérivée.

Durant le XVIIIe siècle, les travaux des mathématiciens Euler et Lagrange mènent au calcul des variations, une branche de l'analyse fonctionnelle regroupant plusieurs méthodes d'optimisation. Ce dernier invente une technique d'optimisation sous contraintes: Les multiplicateurs de Lagrange.

Le XIXe siècle est marqué par l'intérêt croissant des économistes pour les mathématiques. Ceux-ci mettent en place des modèles économiques qu'il convient d'optimiser, ce qui accélère le développement des mathématiques. Depuis cette période, l'optimisation est devenue un pilier des mathématiques appliquées et le foisonnement des techniques est tel qu'il ne saurait être résumé en quelques lignes.

On peut tout de même évoquer l'invention de plusieurs méthodes itératives utilisant le gradient de la fonction, ainsi que l'utilisation du terme programmation mathématique, pour désigner des problèmes d'optimisation.

Historiquement, le premier terme introduit fut celui de programmation linéaire, inventé par George Dantzig vers 1947^[4]. Le terme programmation dans ce contexte ne réfère pas à la programmation informatique (bien que les ordinateurs soient largement utilisés de nos jours pour résoudre des programmes mathématiques). Il vient de l’usage du mot programme par les forces armées américaines pour établir des horaires de formation et des choix logistiques, que Dantzig étudiait à l’époque. L’emploi du terme programmation avait également un intérêt pour débloquer des crédits en une époque où la planification devenait une priorité des gouvernements. L'expression programmation mathématique, qui requiert la longue explication ci-dessus, tend à être abandonnée. Par exemple, en juin 2010, la société savante internationale qui représente cette discipline a vu son nom précédent Mathematical Programming Society changé en Mathematical Optimization Society ; pour la même raison, on préfère aujourd'hui utiliser les locutions optimisation linéaire/quadratique/... au lieu de programmation linéaire/quadratique/....

Annexes

Notes et références

↑ Catherine Vayssade, « Optimisation mécanique, Optimisation topologique », 2004. Consulté le 24 décembre 2008
↑ http://www.apmep.asso.fr/IMG/pdf/Lu-33-Xhonneux-LaRochelle.pdf
↑ Voir l'article Méthode de Newton
↑ (en) G.B. Dantzig (1951). Maximization of a linear function of variables subject to linear inequalities. In Tj.C. Koopmans, éditeur, Activity Analysis of Production and Allocation, pages 339–347. Wiley, New York.

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Optimization (mathematics) » (voir la liste des auteurs)
Mathematical Optimization Society est la société savante internationale associée à cette discipline.

Ouvrages généraux

(en) J. F. Bonnans, J. Ch. Gilbert, C. Lemaréchal, C. Sagastizábal (2006), Numerical Optimization - Theoretical and Numerical Aspects [détail des éditions]
(en) Bonnans, J. F et Shapiro, A. (2000), Perturbation analysis of optimization problems. Springer. ISBN: 978-0-387-98705-7.
Michel Minoux, Programmation mathématique - théorie et algorithmes, éditions Dunod, 1983 (ISBN 2040154876)
(en) Encyclopedia of Optimization, Floudas, Christodoulos A.; Pardalos, Panos M. (éditeurs), 2e édition, 2009 (ISBN 978-0-387-74758-3)

Liens externes

(en) Guide NEOS
(en) Mathematical Optimization Society : la société savante internationale d'optimisation mathématique.

Portail des mathématiques

Catégorie :

Optimisation

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Optimisation (mathématiques) de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires: