Optimisation Multidisciplinaire

L'Optimisation multidisciplinaire (OMD ou MDO en anglais) est un domaine d'ingénierie qui utilise des méthodes d'optimisation afin de résoudre des problèmes de conception mettant en œuvre plusieurs disciplines.

La MDO permet aux concepteurs d'incorporer les effets de chacune des disciplines en même temps. L'optimum global ainsi trouvé est meilleur que la configuration trouvée en optimisant chaque discipline indépendamment des autres, car l'on prend en compte les interactions entre les disciplines. Cependant cela entraîne un surcoût au niveau du temps calcul et de la complexité du problème.

Ces techniques sont utilisées dans plusieurs domaines d'application, dont la conception automobile, navale, électronique et informatique. Cependant la plus grande application reste dans le domaine de la conception aéronautique. Par exemple, le projet d'aile volante de Boeing (Blended wing body) a utilisé largement les techniques MDO dans le cadre de la conception avant projet. Les disciplines considérées dans ce projet sont l'aérodynamique, la mécanique des structures, la propulsion et l'économie.

Histoire

Traditionnellement, la conception aéronautique est effectuée par équipes, possédant chacune des experts et des connaissances spécifiques dans un domaine précis, comme l'aérodynamique ou la structure. Chaque équipe s'attache à obtenir un point de conception acceptable en travaillant séquentiellement. Par exemple l'aérodynamique souhaite obtenir un certain champ de pression sur l'aile et la structure cherchera un profil d'aile qui y parviendra. Les buts à atteindre sont généralement de minimiser la traînée ou le poids.

Entre 1970 et 1990, deux facteurs ont changé l'approche de la conception. La Conception assistée par ordinateur (CAO), qui permet de modifier et d'analyser rapidement les points de conception. Le second est le changement de politique de gestion dans la plupart des compagnies aériennes et des organisations militaires, avec des performances concernant les coûts engendrés durant le cycle de vie des véhicules. Ceci a entrainé la création de nouveau facteurs économiques tels la faisabilité, la possibilité d'usiner et de maintenir les configurations obtenues, etc.

Depuis les années 1990, ces techniques ont migré vers les autres industries. La mondialisation a conduit à des conceptions de plus en plus distribuées et décentralisées. La puissances des micro-ordinateurs remplacent les supercomputeurs centralisés, la communication et le partage des informations sont facilités par internet et les réseaux locaux. Les outils d'analyse haute fidélité, de type éléments finis, commencent à être très performant. De plus, il y a de grandes avancées dans le domaine des algorithmes d'optimisation.

Les formulations MDO

Cette partie est la plus difficile dans ces procédés. On recherche un compromis entre un système totalement couplé, c’est-à-dire où la physique interdisciplinaire est bien définie pour chacun des points de l'optimisation, mais qui engendre un grand coût en matière de temps de calcul et un système où l'on relaxe les variable de couplage et où la faisabilité interdisciplinaire est exigée seulement à la convergence.

Les méthodes de résolution d’un problème d’optimisation multidisciplinaire peuvent être divisées en deux catégories : les méthodes mononiveaux (ou single-level) et les méthodes multiniveaux. Les méthodes mononiveaux font appel à un unique optimiseur.

• Parmi les méthodes mononiveaux, on trouve les méthodes AAO (All At Once), MDF (Multi Discipline Feasible), IDF (Individual Discipline Feasible).
• Parmi les méthodes multiniveaux : CO (Collaborative Optimisation), CSSO (Concurrent Sub Space Optimisation), BLISS (Bi Level Integrated System Synthesis).

Variable de conception

Une variable de conception est une valeur numérique que le designeur peut modifier. Par exemple l'épaisseur du caisson ou bien la flèche peut être considérée comme variable de conception. Ces variables peuvent être continues, ou discrètes (nombre de moteurs sur l'avion).

On peut aussi séparer les variables locales, qui n'interviennent que dans une discipline, des variables partagées, qui ont une influence sur plusieurs disciplines.

Contrainte

Une contrainte est une condition qui doit être satisfaite pour obtenir un point admissible.

Un exemple dans la conception aéronautique : la portance de l'avion doit être égale au poids. En plus de traduire des phénomènes physiques ces contraintes peuvent aussi représenter des limitations de ressources, des exigences des cahiers des charges, ou des limites de validité du modèle d'analyse.

Objectifs

Un objectif est une valeur numérique qui doit être optimisée. Par exemple, le concepteur peut choisir de maximiser le profit, le rayon d'action, ou bien de minimiser le poids total. D'autres problèmes traitent de multiobjectif, souvent contradictoires. La solution sera alors choisie par des expert en trouvant un compromis à l'aide de front de pareto.

Modèles

Les concepteurs doivent aussi choisir des modèles afin de représenter le comportement des contraintes et des objectifs selon les variables de conception. On peut avoir des modèles empiriques, comme une analyse régressive sur le coût des avion, ou bien des modèles théoriques plus poussés, comme les éléments finis ou la CFD, ou bien encore des modèles réduits en tout genre. Le choix de ces modèles résulte d'un compromis entre temps d'exécution et précision de l'analyse.

Le caractère multidisciplinaire du problème complique fortement le choix des modèles et leur implémentation. Bien souvent de nombreuses itérations sont nécessaires avant de trouver les bonnes valeurs des fonctions coûts et des contraintes. En effet, le champ de pression modifiera la forme de l'aile et cette dernière affectera ce même champ. Il faut donc évaluer séquentiellement ces valeurs, avant de pouvoir converger vers la bonne configuration de la physique.

Formulation Standard

Une fois que l'on a choisi les variables de conception, les contraintes, les objectifs et les relations entre chaque discipline, le problème général peut s'exprimer de la manière suivante :

trouver 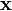qui minimise 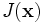sous contrainte 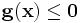et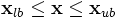

où J est un objectif, 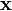est un vecteur de variable de conception, 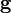est le vecteur des contraintes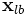, et et 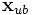sont les bornes des variables de conception.

Résolution du problème

Le problème est alors résolu en appliquant les techniques d'optimisation appropriées. Cela peut être des algorithmes à base de gradient ou bien des algorithmes génétiques.

La plupart de ces méthodes demandent un grand nombre d'évaluations des objectif et des contraintes. Chaque modèle peut être assez coûteux en temps de calcul. Il faut alors utiliser des technique de parallélisation de calcul et des surfaces de réponse.

Il faut préciser enfin qu'il n'existe pas de solution miracle garantissant de trouver l'optimum global en un temps raisonnable. Les méthodes à base de gradient se retrouvent facilement coincées dans un optimum local. Les méthodes stochastiques, comme les algorithmes génétiques ont de fortes chances d'obtenir une solution correcte, nécessitant un nombre d'évaluations de fonctions exponentiellement proportionnel au nombre de variables de conception et ne garantissant pas de bonnes propriétés d'optimalité. Une méthode hybride pourrait pallier ces deux difficultés.

L'optimisation multidisciplinaire est très en vogue dans la recherche en aéronautique, en informatique et en mathématique appliquée.