Recuit simule

Le recuit simulé est une métaheuristique inspirée d'un processus utilisé en métallurgie. Ce processus alterne des cycles de refroidissement lent et de réchauffage (recuit) qui tendent à minimiser l'énergie du matériau. Elle est aujourd'hui utilisée en optimisation pour trouver les extrema d'une fonction.

Elle a été mise au point par trois chercheurs de la société IBM, S. Kirkpatrick, C.D. Gelatt et M.P. Vecchi en 1983, et indépendamment par V. Cerny en 1985.

Sommaire 1 Recuit réel 2 Déroulement du processus 2.1 État initial de l'algorithme 2.2 Itérations de l'algorithme 2.3 Programme de recuit 2.4 Pseudo-code 2.5 Inconvénients 3 Étude théorique 4 Applications 5 Exemple sous Mathematica 6 Notes et références 7 Voir aussi

Recuit réel

La description des phénomènes physiques et quantiques liés au processus de recuit s'appuie sur la statistique de Boltzmann.

Déroulement du processus

Le recuit simulé s'appuie sur l'algorithme de Metropolis-Hastings, qui permet de décrire l'évolution d'un système thermodynamique. Par analogie avec le processus physique, la fonction à minimiser deviendra l'énergie E du système. On introduit également un paramètre fictif, la température T du système.

Partant d'une solution donnée, en la modifiant, on en obtient une seconde. Soit celle-ci améliore le critère que l'on cherche à optimiser, on dit alors qu'on a fait baisser l'énergie du système, soit celle-ci le dégrade. Si on accepte une solution améliorant le critère, on tend ainsi à chercher l'optimum dans le voisinage de la solution de départ. L'acceptation d'une « mauvaise » solution permet alors d'explorer une plus grande partie de l'espace de solution et tend à éviter de s'enfermer trop vite dans la recherche d'un optimum local.

État initial de l'algorithme

La solution initiale peut être prise au hasard dans l'espace des solutions possibles. À cette solution correspond une énergie initiale E = E₀. Cette énergie est calculée en fonction du critère que l'on cherche à optimiser. Une température initiale T = T₀ élevée est également choisie. Ce choix est alors totalement arbitraire et va dépendre de la loi de décroissance utilisée.

Itérations de l'algorithme

À chaque itération de l'algorithme une modification élémentaire de la solution est effectuée. Cette modification entraîne une variation Δ_E de l'énergie du système (toujours calculée à partir du critère que l'on cherche à optimiser). Si cette variation est négative (c'est-à-dire qu'elle fait baisser l'énergie du système), elle est appliquée à la solution courante. Sinon, elle est acceptée avec une probabilité 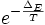. Ce choix de l'exponentielle pour la probabilité s'appelle règle de Metropolis.

On itère ensuite selon ce procédé en gardant la température constante.

Programme de recuit

Deux approches sont possibles quant à la variation de la température :

1. Pour la première, on itère en gardant la température constante. Lorsque le système a atteint un équilibre thermodynamique (au bout d'un certain nombre de changements), on diminue la température du système. On parle alors de paliers de température.
2. La seconde approche fait baisser la température de façon continue. On peut alors imaginer toute sorte de loi de décroissance. La plus courante étant T_{i + 1} = X * T_i avec X < 1 (assez couramment X = 0.99).

Dans les 2 cas, si la température a atteint un seuil assez bas fixé au préalable ou que le système devient figé, l'algorithme s'arrête.

La température joue un rôle important. À haute température, le système est libre de se déplacer dans l'espace des solutions ( 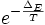proche de 1) en choisissant des solutions ne minimisant pas forcément l'énergie du système. À basse température, les modifications baissant l'énergie du système sont choisies, mais d'autres peuvent être acceptées, empêchant ainsi l'algorithme de tomber dans un minimum local.

Pseudo-code

Le pseudo-code suivant met en œuvre le recuit simulé tel que décrit plus haut, en commençant à l'état s0 et continuant jusqu'à un maximum de kmax étapes ou jusqu'à ce qu'un état ayant pour énergie emax ou moins est trouvé. L'appel voisin(s) génère un état voisin aléatoire d'un état s. L'appel aléatoire() renvoie une valeur aléatoire dans l'intervalle [0, 1]. L'appel temp(r) renvoie la température à utiliser selon la fraction r du temps total déjà dépensé.

s := s0
e := E(s)
k := 0
tant que k < kmax et e > emax
  sn := voisin(s)
  en := E(sn)
  si en < e ou aléatoire() < P(en - e, temp(k/kmax)) alors
    s := sn; e := en
  k := k + 1
retourne s

Inconvénients

Les principaux inconvénients du recuit simulé résident dans le choix des nombreux paramètres, tels que la température initiale, la loi de décroissance de la température, les critères d'arrêt ou la longueur des paliers de température. Ces paramètres sont souvent choisis de manière empirique.

Étude théorique

Des études théoriques du recuit simulé ont pu montrer que sous certaines conditions, l'algorithme du recuit convergeait vers un optimum global^[1]. Ce résultat est important car il nous assure, contrairement à d'autres métaheuristiques, que le recuit simulé peut trouver la meilleure solution, si on le laisse chercher indéfiniment.

Applications

Comme pour toute métaheuristique, la méthode trouve son application dans de nombreux domaines dans lesquels on a à résoudre des problèmes d'optimisation difficile. On peut citer entre autres la conception des circuits électroniques (placement-routage) ou l'organisation de réseaux informatiques.

Exemple sous Mathematica

   F[X_] = Abs[X1] + Abs[X2];
    g[T_] = N[T^0.99];

        Recuit[F_, g_,Xi_,Ti_,Tf_,Ampli_,MaxTconst_,itermax_] := Module[{T,Xopt,iter=1,DF,p,L,X,compteur},
     	   X = Xi; T = Ti; L = {Xi}; Xopt = X;
         While [T > Tf && iter < itermax,
          compteur = 1;
           While[compteur < MaxTconst,
             Y = X + Table[Ampli*Random[Real, {-1, 1}], {i, 1, Length[X]}];
             DF = F[Y] - F[X];
              If[DF < 0, X = Y; AppendTo[L, X];
                If[F[X] < F[Xopt], Xopt = X],
                p = Random[];];
              If [p ≤ Exp[-DF/T], X = Y; AppendTo[L, X]];
              compteur = compteur + 1;
              ];
            T = g[T];
            iter = iter + 1;
            ];
          Return[L]
          ];
    
    resR = Recuit[F, g, {2, 3}, 10, 1, 0.5, 1.5, 1000];
    ListPlot[resR, PlotJoined -> True];

Notes et références

Voir aussi

• Retour sur trace

• Portail de l’informatique
• Portail des mathématiques