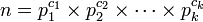Nombre hautement compose

Nombre hautement composé

Un nombre hautement composé est un entier qui possède plus de diviseurs que n'importe quel entier positif inférieur à lui.

Les vingt-et-un premiers nombres hautement composés sont :

nombres hautement composés (suite A002182 de l’OEIS)	1	2	4	6	12	24	36	48	60	120	180	240	360	720	840	1260	1680	2520	5040	7560	10080	...
nombres de diviseurs (suite A002183 de l’OEIS)	1	2	3	4	6	8	9	10	12	16	18	20	24	30	32	36	40	48	60	64	72	...
décomposition en facteurs premiers	1	2	2²	2 3	2² 3	2³ 3	2² 3²	2⁴ 3	2² 3 5	2³ 3 5	2² 3² 5	2⁴ 3 5	2³ 3² 5	2⁴ 3² 5	2³ 3 5 7	2² 3² 5 7	2⁴ 3 5 7	2³ 3² 5 7	2⁴ 3² 5 7	2³ 3³ 5 7	2⁵ 3² 5 7	...

Il existe une infinité de nombres hautement composés.

Cette proposition se démontre très facilement. Supposons que n est un nombre hautement composé arbitraire. Alors 2n possèdera plus de diviseurs que n (2n est un diviseur et sont tous les diviseurs de n) et ainsi, certains nombres plus grands que n (mais pas plus grand que 2n) doivent donc être hautement composés.

Une autre démonstration, encore plus élémentaire, consiste à considérer, pour n donné, l'ensemble des nombres ayant au moins n diviseurs, qui est non vide (car il contient au moins 2^n–1, donc admet un plus petit élément (l'ordre canonique sur l'ensemble des naturels étant bien fondé), qui est par construction hautement composé.

Pour donner une idée de la forme d'un nombre hautement composé, on peut dire qu'il s'agit d'un nombre possédant des facteurs premiers aussi petits que possible, sans être trop de fois les mêmes. En effet, si l'on considère la décomposition d'un nombre n en facteurs premiers comme suit :

$n = p_1^{c_1} \times p_2^{c_2} \times \cdots \times p_k^{c_k}$

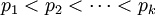avec $p_1 < p_2 < \cdots < p_k$ premiers, et des exposants $c i$ entiers non nuls. Alors, le nombre de diviseurs de n est exactement:

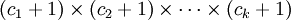$(c_1 + 1) \times (c_2 + 1) \times \cdots \times (c_k + 1)$ .

Par conséquent, pour que n soit hautement composé:

il faut que les nombres premiers cités soient les k plus petits nombres premiers (2, 3, 5, ...) ; sinon, on pourrait remplacer un des $p i$ par un nombre premier plus petit, et obtenir un nombre inférieur à n ayant le même nombre de diviseurs (par exemple 10=2×5 peut être remplacé par 6=2×3, chacun a 4 diviseurs) ;
il faut que $c_1 \geq c_2 \geq \cdots \geq c_k$ ; sinon, en échangeant les deux exposants fautifs on diminue n tout en conservant le même nombre de diviseurs (par exemple 18=2¹×3² peut être remplacé par 12=2²×3¹, chacun a 6 diviseurs).

On peut aussi montrer qu'il faut que c_k = 1, sauf dans deux cas particuliers n=4 et n=36.

Les nombres hautement composés supérieurs à 6 sont aussi des nombres abondants. Un seul coup d'œil aux trois ou quatre plus hauts diviseurs d'un nombre hautement composé particulier est nécessaire pour confirmer ce fait. Les nombres hautement composés sont également décomposables en produits de primorielles.

Beaucoup de ces nombres sont utilisés dans les systèmes traditionnels de mesure, et ont tendance à être utilisés en ingénierie, en raison de leur usage dans les calculs de fractions compliquées.

Si Q(x) représente la quantité de nombres hautement composés qui sont inférieurs ou égaux à x, alors il existe deux constantes b et c, toutes les deux plus grandes que 1, nous avons

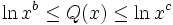${\ln x}^b \le Q(x) \le {\ln x}^c\,\!$ .

La première partie de l'inégalité fut prouvée par Paul Erdős en 1944 et la seconde partie par J.-L. Nicholas en 1988.

Sommaire

1 Exemple
2 Voir aussi
- 2.1 Articles connexes
- 2.2 Liens externes

Exemple

Exemple du nombre hautement composé : 10080 10080 = (2 × 2 × 2 × 2 × 2) × (3 × 3) × 5 × 7 qui n'a pas moins de 72 diviseurs.
1 × 10080	2 × 5040	3 × 3360	4 × 2520	5 × 2016	6 × 1680
7 × 1440	8 × 1260	9 × 1120	10 × 1008	12 × 840	14 × 720
15 × 672	16 × 630	18 × 560	20 × 504	21 × 480	24 × 420
28 × 360	30 × 336	32 × 312	35 × 288	36 × 280	40 × 252
42 × 240	45 × 224	48 × 210	56 × 180	60 × 168	63 × 160
70 × 144	72 × 140	80 × 126	84 × 120	90 × 112	96 × 105

Les nombres en gras sont eux-mêmes des nombres hautement composés.
Seul le vingtième nombre hautement composé 7560 (=3×2520) est absent.

10080 est également un nombre de facteurs premiers inférieurs à sept.
C'est alors un nombre 7-lisse, cf. suite A002473 de l’OEIS.

Voir aussi

Liens externes

Ensembles d'entiers sur la base de leur divisibilité
Formes de factorisation :	Nombre premier · Nombre composé · Nombre puissant · Entier sans facteur carré
Sommes de diviseurs :	Nombre parfait · Nombre presque parfait · Nombre quasi parfait · Nombre parfait multiple · Nombre hyperparfait · Nombre parfait unitaire · Nombre semi-parfait · Nombre semi-parfait primitif · Nombre pratique
Nombres de diviseurs :	Nombre abondant · Nombre hautement abondant · Nombre superabondant · Nombre colossalement abondant · Nombre hautement composé
Autres :	Nombre déficient · Nombre étrange · Nombre amical · Nombre sociable · Nombre solitaire · Nombre sublime · Nombre à moyenne harmonique entière · Nombre frugal · Nombre équidigital · Nombre extravagant

Portail des mathématiques

Ce document provient de « Nombre hautement compos%C3%A9 ».

Catégorie : Propriété arithmétique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nombre hautement compose de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Nombre Hautement Composé — Un nombre hautement composé est un entier qui possède plus de diviseurs que n importe quel entier positif inférieur à lui. Les vingt et un premiers nombres hautement composés sont : nombres hautement composés (suite A002182 de l’OEIS) 1 2 4… … Wikipédia en Français
Nombre hautement composé — Un nombre hautement composé est un entier qui possède plus de diviseurs que n importe quel entier positif inférieur à lui. Les vingt et un premiers nombres hautement composés sont : nombres hautement composés (suite A002182 de l’OEIS) 1 2 4… … Wikipédia en Français
Nombre Hautement Indicateur — Un nombre hautement indicateur k est un nombre entier qui possède plus de solutions pour l équation , où est l indicatrice d Euler, que n importe quel entier inférieur à lui. Les premiers petits nombres hautement indicateurs sont : 1, 2, 4,… … Wikipédia en Français
Nombre hautement indicateur — Un nombre hautement indicateur k est un nombre entier qui possède plus de solutions pour l équation , où est l indicatrice d Euler, que n importe quel entier inférieur à lui. Les premiers petits nombres hautement indicateurs sont : 1, 2, 4,… … Wikipédia en Français
Nombre Composé — Un nombre composé est un nombre entier positif qui possède un diviseur positif autre que un ou lui même. Par définition, chaque entier plus grand que un est soit un nombre premier, soit un nombre composé. Les nombres zéro et un ne sont considérés … Wikipédia en Français
Nombre compose — Nombre composé Un nombre composé est un nombre entier positif qui possède un diviseur positif autre que un ou lui même. Par définition, chaque entier plus grand que un est soit un nombre premier, soit un nombre composé. Les nombres zéro et un ne… … Wikipédia en Français
Nombre Parfait — Un nombre parfait est un nombre entier n strictement supérieur à 1 qui est égal à la somme de ses diviseurs stricts, autrement dit, tel que où σ(n) est la somme des diviseurs entiers positifs de n, n non compris. Le premier nombre parfait est 6,… … Wikipédia en Français
Nombre Abondant — En mathématiques, un nombre abondant est un nombre entier naturel n qui est strictement inférieur à la somme de ses diviseurs stricts, autrement dit, tel que où est la somme des diviseurs entiers positifs de n y compris n. Les nombres abondants… … Wikipédia en Français
Nombre Déficient — En mathématiques, un nombre déficient est un nombre entier naturel n qui est strictement supérieur à la somme de ses diviseurs stricts, autrement dit, tel que σ(n) < 2n où σ(n) est la somme des diviseurs entiers positifs de n y compris n . La… … Wikipédia en Français
Nombre Hyperparfait — En mathématiques, un nombre k hyperparfait (quelquefois simplement appelé nombre hyperparfait) est un nombre naturel n pour lequel l égalité reste valable, où est la fonction diviseur (c.a.d., la somme de tous les diviseurs positifs de n). Un… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Nombre hautement compose

Nombre hautement composé

Sommaire

Exemple

Voir aussi

Articles connexes

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Nombre hautement compose

Nombre hautement composé

Sommaire

Exemple

Voir aussi

Articles connexes

Liens externes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link