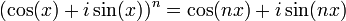De Moivre

Abraham de Moivre

Abraham de Moivre
Naissance	26 mai 1668 Vitry-le-François (France)
Décès	27 novembre 1754 Londres (Angleterre)
Domicile	Angleterre
Nationalité	Française
Champs	mathématicien
Institution	Royal Society
Célèbre pour	formule de Stirling, Théorème de Moivre-Laplace, Formule de De Moivre
modifier

Abraham de Moivre (né le 26 mai 1667 à Vitry-le-François - mort le 27 novembre 1754 à Londres) est un mathématicien français.

Sommaire 1 En France 2 L'exil 3 Anecdotes 4 Œuvres 5 Notes & références 6 Voir aussi 7 Liens externes

En France

Né d'un père médecin, De Moivre vint au jour dans une famille protestante aisée. Il fut élevé à l'école catholique des frères Chrétiens de Vitry.

A l'âge de onze ans, ses parents l'envoyèrent à l'académie protestante de Sedan, où il étudia le grec sous la férule de Du Rondel. En dépit de l'Édit de Nantes, l'académie protestante de Sedan fut supprimée en 1682 et de Moivre contraint d'étudier la logique à Saumur jusqu'en 1684.

Ses parents déménagèrent pour Paris et il continua ses études au Collège d'Harcourt. Vers cette époque, De Moivre lit les traités de Huygens, prend des cours de physique, et s'entraîne en mathématiques sous la direction (privée) d' Ozanam.

En 1685, à la révocation de l'Édit de Nantes, l'expulsion des Huguenots se généralise. De Moivre est emprisonné jusqu'au 27 avril 1688 pour raison religieuse au prieuré de St Martin. Peu après, il émigre vers l'Angleterre.

L'exil

Il y vécut assez chichement les premières années, enseignant à domicile et dans les "coffe house" de Londres. Après une visite au comte du Devonshire, il découvrit les Principia de Newton. Dès lors, il ne s'en sépara plus (on prétend qu'il en découpait des pages pour l'emporter avec lui).

En 1692, De Moivre rencontra Halley, assistant de la Royal Society, et peu après Newton, avec qui il se lia d'amitiés. A la suite de quoi, De Moivre se livra entièrement à la théorie des fluxions. En 1673, Il fit la connaissance de Leibniz, qui essaya (sans succès) d'obtenir pour lui un poste en Allemagne En Mars 1695, Halley communiqua son article : Method of fluxions à la Royal Society.

En 1697, il fut élu membre de la Royal Society de Londres (l'équivalent de l'Académie des sciences de Paris).

En 1710, De Moivre fut appointé par la Royal Society pour trancher les querelles entre Newton et Leibniz... Désespérant d'obtenir une chaire à Cambridge il demanda le soutien de Leibniz auprès de Johann Bernoulli,en vain, car Leibniz ne pouvait rien pour lui, pas plus que Newton ou Halley, vu ses origines françaises.

La fin de sa vie se passa en publications. Célibataire, il trouvait sa récréation dans la paix de l'étude, particulièrement dans la littérature. Il eût aimé être Molière avant que d’être Newton , aimait-il à dire. Il connaissait Rabelais presque par coeur. Le 27 juin 1754, Il est élu membre étranger de l' académie des sciences de Paris. Il meurt dans l’anonymat le 27 novembre de la même année.

Anecdotes

Comme Cardan, De Moivre est connu pour avoir prédit le jour de sa mort : il compta qu'il dormait quinze minutes de plus chaque nuit. Sommant cette progression arithmétique, il en déduisit qu'il mourrait lorsque ses nuits feraient vingt-quatre heures. Ce qui se produisit bel et bien.

Alors qu'on lui demandait des renseignements sur la théorie des Fluxions, Newton aurait affirmé : "Go to Mr De Moivre; he knows these things better than I do"

Œuvres

De Moivre était un précurseur du développement de la géométrie analytique et de la théorie des probabilités. Il publia The Doctrine of Chance (Théorie du Hasard) en 1718. Une querelle faillit éclater à ce sujet car il reprenait les travaux du français Montmort : Essay d'analyse sur les jeux de hazard (1708) Il en avait eu connaissance par Huygens. Toutefois la querelle prit fin rapidement car De Moivre généralise ces travaux. En outre, la première définition de l'indépendance statistique apparaît dans cet ouvrage, ainsi que de nombreux problèmes, par exemple à propos de jeux de dés et beaucoup d'autres jeux.

Il a également étudié les statistiques de mortalité et la base de la théorie des annuités (avec Halley).

Dans Miscellanea Analytica (1730) apparaît sous sa forme définitive la formule de Stirling que James Stirling avait indiquée quelques mois plus tôt, et que de Moivre utilisa en 1733 pour décrire la courbe normale comme une approximation de la binomiale^[1]. Dans une seconde édition de l'ouvrage en 1738, de Moivre crédite Stirling d'une amélioration de la formule.

On se souvient également de De Moivre pour sa formule découverte en 1707, que l'on trouve aussi bien en trigonométrie qu'en analyse :

Notes & références

Voir aussi

• Formule de De Moivre
• Principe d'inclusion-exclusion de Moivre

Liens externes

• (fr) Biographie d'Abraham de Moivre sur le site BibM@th.net
• (en) d'Abraham de Moivre sur le site de Saint Andrews
• (en) Biographie d'Abraham de Moivre sur le site de Britanica.

• Portail de la France
• Portail des mathématiques
• Portail du protestantisme