- Partie reelle
-
Partie réelle
Symbole R en écriture Fraktur
En mathématiques, la partie réelle d’un nombre complexe z qui s'écrit sous la forme z = x + iy (où x et y sont des réels) est x. Autrement dit, si le nombre complexe z a pour image le point de coordonnées (x,y) dans le plan, alors sa partie réelle est x. Il s'agit d'un nombre réel.
La partie réelle est notée Re{z} ou
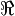{z}, où 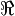est un R capital en caractères Fraktur. La fonction complexe qui associe à z la partie réelle de z n'est pas holomorphe.En utilisant la notion de conjugué
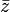d'un nombre complexe z, la partie réelle de z est égale à 
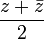.Pour un nombre complexe sous forme polaire, z = (r,θ), les coordonnées cartésiennes (algébriques) sont z = (rcosθ,rsinθ), ou de façon équivalente, z = r(cosθ + isinθ). Il découle de la formule d'Euler que z = reiθ, et donc que la partie réelle de reiθ est rcosθ.
Les calculs avec des fonctions périodiques réelles comme celles des courants alternatifs et des champs électromagnétiques sont simplifiées par leur notation comme parties réelles de fonctions complexes (comme par exemple les phaseurs).
De façon semblable, les calculs de trigonométrie peuvent souvent être simplifiés en représentant les sinusoïdes comme la partie réelle d'une expression complexe, sur laquelle on effectue les calculs. Par exemple :
Voir aussi
Portail des mathématiques
Catégories : Analyse réelle | Nombre complexe
![\begin{align}
\cos(n\theta)+\cos[(n-2)\theta] & = \operatorname{Re}\left\{e^{in\theta} + e^{i(n - 2)\theta}\right\} \\
& = \operatorname{Re}\left\{(e^{i\theta} + e^{-i\theta})\cdot e^{i(n - 1)\theta}\right\} \\
& = \operatorname{Re}\left\{2\cos(\theta) \cdot e^{i(n - 1)\theta}\right\} \\
& = 2\cos(\theta) \cdot \operatorname{Re}\left\{e^{i(n - 1)\theta}\right\} \\
& = 2 \cos(\theta)\cdot \cos[(n - 1)\theta].
\end{align}](/pictures/frwiki/54/6f22c39c91d98cf6fdcbb2d4b45f5cb8.png)
Wikimedia Foundation. 2010.
