Nicolas Oresme

Nicole Oresme
Surnom(s)	L’« Einstein du XIVe siècle »
Naissance	1325 Bayeux
Décès	11 juillet 1382 (à 57 ans) Lisieux
Nationalité	France
Profession(s)	Évêque

Nicole Oresme, né à Bayeux vers 1325 et mort à Lisieux le 11 juillet 1382, est un économiste, mathématicien, physicien, astronome, philosophe, psychologue, musicologue, théologien et traducteur français.

Biographie

Je ne sais donc que je ne sais rien^[1].

Surnommé l’« Einstein du XIV^e siècle », ce savant en avance sur son temps, dont les idées préludaient à celles de la Renaissance, a été un des principaux fondateurs^[2] et vulgarisateurs des sciences modernes, et probablement le penseur le plus original de son siècle. On ne sait pratiquement rien sur sa famille. Le fait qu’il ait fait ses études au Collège de Navarre, établissement commandité et subventionné par le roi pour les étudiants trop pauvres pour payer leurs frais de scolarité à l’université de Paris constitue une indication probable de ses origines paysannes. Toute sa vie se déroula durant la guerre de Cent Ans, la Normandie étant alors souvent occupée par l’Angleterre.

Il étudie les « artes » à Paris (avant 1348), avec Jean Buridan (reconnu comme le fondateur de l’école française de philosophie naturelle), Albert de Saxe et peut-être Marsile d'Inghen et reçoit son Magister Artium. En 1348, il étudie la théologie à Paris. Il obtient son doctorat en 1356 et devient, la même année, grand-maître du Collège de Navarre.

La plupart de ses traités latins les plus intéressants datent d’avant 1360 et prouvent que c’était déjà un universitaire établi à la réputation la plus élevée, qui a attiré l'attention de la famille royale et l’a mis en contact intime avec le futur Charles V en 1356. À partir de 1356, pendant la captivité de son père Jean II en Angleterre, Charles a été régent puis roi de France de 1364 à 1380. Le 2 novembre 1359, il devient secrétaire du roi avant de devenir par la suite, aumônier et conseiller du roi.

Une longue tradition mais non prouvée fait également de lui le précepteur du Dauphin, futur Charles V qui semble avoir tenu le caractère et les talents de Nicole Oresme en très haute estime, a souvent suivi ses conseils et l’a fait rédiger de nombreuses œuvres en français afin de populariser les sciences et de développer le goût de l’érudition dans son royaume. C’est à son insistance qu’il a prononcé un discours dénonçant les désordres de l’Église devant la cour papale d’Avignon. La force de l’influence probable de la pensée politique, économique, morale et philosophique progressiste de Nicole Oresme sur le roi Charles « Le Sage » dont il a été l’ami et le conseiller intime, jusqu’à la mort de ce dernier, reste encore à être étudiée. Il était, à la cour de Charles V qui utilisa souvent ses grandes compétences en matière diplomatique, la personne la plus importante d’un cercle choisi d’intellectuels comprenant, entre autres, Raoul de Presles, Philippe de Mézières.

Son envoi en mission par le dauphin en 1356, puis en 1360 pour solliciter un prêt auprès des autorités municipales rouennaises prouve la confiance royale dans ses capacités. En 1361, alors qu’il était encore grand-maître du Collège de Navarre, il est nommé, avec l’appui de Charles, archidiacre de Bayeux. On sait que cet universitaire passionné a rendu à contrecœur son poste convoité de grand-maître. Le 23 novembre 1362, l’année où il devient maître en théologie, il est nommé chanoine de cathédrale de Rouen. Au moment de sa nomination à ce poste, il enseigne toujours régulièrement à l’université de Paris. Le 10 février 1363, il est nommé chanoine à la Sainte Chapelle, reçoit un demi-bénéfice et est élevé le 18 mars 1364 au poste de doyen de la cathédrale de Rouen. Il est probable que le dauphin Charles a influencé par ses suggestions les décisions de son père Jean II touchant aux fréquents changements de postes d’Oresme.^[3]

Ces postes consécutifs à la cathédrale de Rouen (1364-77) ne l’empêchent pas de passer beaucoup de temps, particulièrement pour les affaires universitaires, à Paris, sans que les nombreux documents attestant de sa présence dans la capitale prouvent qu’il y enseignait également. Des lettres envoyées par Charles V à Rouen du 28 août au 11 novembre 1372 établissent une coïncidence entre le début de son séjour ininterrompu à Paris et le commencement de ses activités de traduction prolongées à la demande du roi. Sa résidence à Paris semble avoir été prolongée par Charles V jusqu’à 1380, lorsqu’il a commencé à travailler en 1369 à sa traduction de l’Éthique d’Aristote, qui semble avoir été achevée en 1370. Celles de la Politique et des Économiques du même philosophe ont pu être accomplies entre les années 1372 et 1374, et le De caelo et mundo en 1377. Ses grands travaux lui ont valu, dès 1371, une pension du trésor royal. Son travail infatigable pour Charles V et la famille royale lui a également valu, avec l’appui du roi, le poste d’évêque de Lisieux, le 3 août 1377. Il n’a pris résidence à Lisieux qu’en septembre 1380 et on ne connaît pas grand chose sur les cinq dernières années de sa vie. Il a été, à sa mort survenue deux ans après celle de Charles V, enterré dans la cathédrale de Lisieux.

Travaux scientifiques

D’après l’ouvrage de Taschow (Nicole Oresme und der Frühling der Moderne, 2003) Nicole Oresme est surtout connu comme économiste, mathématicien, et physicien, mais également comme musicologue, psychologue et philosophe. Ses vues économiques sont contenues dans le Commentaire sur l’éthique d’Aristote, (1370), le Commentaire sur la politique et les économiques d’Aristote, (1371) et le Traité des monnaies (De origine, natura, jure et mutationibus monetarum). Tous trois rédigés en latin et en français, ces ouvrages consacrent, surtout le troisième, leur auteur comme le précurseur de la science de l’économie politique tout en révélant sa maîtrise de la langue française. Ceci fait de lui le pionnier de la terminologie et du langage scientifiques français. Il a créé un grand nombre de termes scientifiques français et a devancé l’utilisation des mots latins dans la langue scientifique du XVIII^e siècle. Un bref survol de l’universalité du travail de Nicole Oresme passe par des domaines tels que les mathématiques, la musicologie, la psychologie, la philosophie naturelle et la physique :

Mathématiques

Ses contributions les plus importantes aux mathématiques sont contenues dans le Tractatus de configuratione qualitatum et motuum, jamais imprimé. Un compendium de cet ouvrage imprimé sous le titre de Tractatus de latitudinibus formarum de Johannes de Sancto Martino (1482, 1486, 1505 et 1515) a été pendant longtemps la seule source d’étude de ses idées mathématiques. Les scolastiques distinguaient, dans une qualité ou une forme accidentelle telle que la chaleur, entre l’intensio (le degré de chaleur à chaque point) et l’extensio (la longueur de la tige chauffée). Ces deux termes étaient souvent remplacés par ceux de latitudo et de longitudo et, dès Thomas d'Aquin jusqu’à une période avancée du XIV^e siècle, la question des latitudo formae a fait l’objet de débats animés jusqu’à ce que Nicole Oresme clarifie la question en utilisant ce qu’on appellerait, en termes modernes, des coordonnées rectangulaires : une longueur proportionnée à la longitudo constituait l’abscisse à un point donné et une perpendiculaire à ce point, proportionnelle à la latitudo constituait l’ordonnée. Oresme a prouvé qu’on pouvait considérer la propriété géométrique d’une telle figure comme correspondant à la propriété de la forme elle-même, les paramètres de latitudo et de longitudo pouvant changer ou demeurer constants. Oresme définit la latitudo uniformis comme ce qui est représenté par une ligne parallèle à la longitude et tout autre latitudo est difformis; la latitudo uniformiter difformis est représentée par une ligne droite inclinée vers l’axe de la longitude. Nicole Oresme a montré que cette définition est équivalente à une relation algébrique dans laquelle figureraient les longitudes et les latitudes de trois points quelconques : en d’autres termes, il donne l’équation de la ligne droite et précède ainsi Descartes de trois siècles dans l’invention de la géométrie analytique. Oresme a étendu cette doctrine aux figures à trois dimensions.

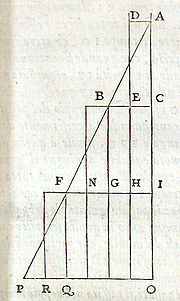Démonstration par Galilée de la loi de l’espace traversé en cas de mouvement uniformément varié. La démonstration est identique à celle à laquelle avait procédé Oresme deux siècles auparavant.

À côté de la longitude et de la latitude d’une forme, il considérait les mensura ou quantitas d’une forme proportionnelle à la surface de la figure qui la représente. Il a prouvé ce théorème : une forme uniformiter difformis a la même quantité qu’une forme uniformis de la même longitude et dont la latitude est la moyenne entre les deux limites extrêmes de la première. Il a ensuite prouvé que sa méthode de figurer la latitude des formes peut s’appliquer au mouvement d’un point, à condition que le temps soit pris comme longitude et la vitesse comme latitude ; l’espace couvert dans un temps donné constitue alors la quantité.

Le théorème de la latitude uniformiter difformis est devenu, en vertu de cette transposition, la loi de l’espace traversé en cas de mouvement uniformément varié. La démonstration est identique à celle à laquelle procédera Galilée au XVII^e siècle. Cette loi n’a d’ailleurs jamais été oubliée durant l’intervalle séparant Oresme de Galilée car elle a été enseignée à Oxford par William Heytesbury et ses disciples, puis à Paris et en Italie, par tous les disciples suivants de cette école. Au milieu du XVI^e siècle, longtemps avant Galilée, le dominicain Domingo de Soto a appliqué cette loi à la chute uniformément accélérée des corps lourds et à l’ascension uniformément décroissante des projectiles.

Dans l’Algorismus proportionum et le De proportionibus proportionum, Oresme a développé la première méthode de calcul des puissances avec des exposantes irrationnelles fractionnelles, c’est-à-dire le calcul avec des proportions irrationnelles (proportio proportionum). La base de cette méthode était l’égalisation des grandeurs continues et des nombres discrets, idée tirée par Oresme de la théorie de la musique monocorde (sectio canonis). Ceci lui a permis de surmonter la prohibition pythagoricienne de la division régulière des intervalles pythagoriciens comme 8/9, 1/2, 3/4, 2/3 et lui a permis de produire la gamme tempérée deux siècles et demi avant Simon Stevin. Exemple de la division égale de l’octave en 12 parties :

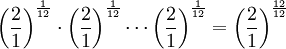
Oresme a utilisé, par exemple, cette méthode dans sa section musicale du Tractatus de configurationibus qualitatum et motuum dans le contexte de sa « théorie de la tonalité partielle ou harmonique (voir ci-dessous) pour produire des proportions de son irrationnelles (timbre laid ou couleur de tonalité) dans la direction du « continuum de tonalité partielle » (« bruit blanc »).^[4]

Oresme s’intéressait beaucoup aux limites, aux valeurs seuil et aux séries au moyen d’additions géométriques (Tractatus de configurationibus qualitatum et motuum, Questiones super geometriam Euclidis) qui ont préparé la voie au calcul infinitésimal de Descartes et de Galilée. Il a prouvé la divergence des série harmoniques au moyen de la méthode standard toujours enseignée dans les cours d’analyse mathématique actuels.

Pour la préfiguration d’Oresme de la stochastique moderne, cf. infra la rubrique « Philosophie naturelle ». Taschow a bien montré comment Nicole Oresme a transformé la méthode graphique, évoquée ci-dessus, de son Tractatus de configurationibus qualitatum et motuum de la théorie musicale de son temps. De là on vient aux importantes contributions d’Oresme dans le domaine de la musicologie.^[5]

Musicologie

On peut voir dans la « configuratio qualitatum et la pluridimensionalité fonctionnelle » qui y est associée, qu’ils sont étroitement liés aux diagrammes musicologiques actuels et, ce qui est primordial, à la notation musicale, qui mesure également et représente visuellement les variations d’un sonus accordant des mesures données d’extensio (intervalles de temps) et d’intensio (ton). Les représentations complexes d’écriture musicale sont devenues, dans l’œuvre d’Oresme, configurationes qualitatum ou difformitates compositae, la musique fonctionnant une fois de plus comme le paradigme légitimateur. Néanmoins, la sphère musicale a non seulement fourni à la théorie d’Oresme une légitimation empirique, elle l’a également aidé à exemplifier les divers types de configurations uniformes et difformes qu’il avait développés, notamment l’idée que les configurationes étaient dotées de qualités avec des effets spécifiques, esthétiques ou autres, dont la représentation géométrique permettrait l’appréhension analytique. Ce dernier point aide à expliquer l’approche esthétique compréhensive d’Oresme des phénomènes normaux, fondée sur la conviction que l’évaluation esthétique de l’expérience sensible (graphiquement représentable) fournissait un principe d’analyse adéquat. Dans ce contexte, la musique a joué, une fois de plus, un rôle important en tant que modèle à l’« esthétique de la complexité et de l’infini » préférée par la mentalité du XIV^e siècle.

Oresme a cherché les paramètres du sonus par l’expérimentation au niveau microstructurel et acoustique de la tonalité simple et au niveau macrostructurel de l’unisson ou de la musique polyphonique. En essayant de capturer analytiquement les divers paramètres physiques, psychologiques et esthétiques des sonus selon l’extensio et l’intensio, Oresme souhaitait les représenter comme conditions aux catégories infiniment variables de pulchritudo et de turpitudo. Il a poussé cette méthode à un niveau qui, représentant la description mathématique la plus complète des phénomènes musicaux avant les Discorsi de Galilée, ne connaît aucun équivalent au Moyen Âge. Il est noter que cette recherche l’a amené à découvrir non seulement les ton partiels ou sons harmoniques trois siècles avant Marin Mersenne, mais également à identifier la relation entre les harmoniques et la couleur de la tonalité, ce qu’il a expliqué dans une théorie physico-mathématique détaillée, dont le niveau de complexité ne devait pas être atteint de nouveau avant le XIX^e siècle avec Hermann von Helmholtz.

Il faut également mentionner l’interprétation mécaniste d’Oresme dans son Tractatus de configuratione et qualitatum motuum du sonus comme un type spécifique discontinu de mouvement (vibration), de résonance comme phénomène d’harmonique et de la relation de consonance et de dissonance, qui dépassait même la théorie réussie mais fausse de la coïncidence de la consonance formulée au XVII^e siècle.

La démonstration d’Oresme d’une correspondance entre une méthode mathématique (configuratio qualitatum et motuum) et un phénomène physique (son) constitue un cas particulièrement rare, à la fois pour le XIV^e siècle, en général, et pour l’œuvre d’Oresme, en particulier. Les sections du Tractatus de configurationibus traitant de la musique constituent des étapes importantes dans le développement de l’esprit de quantification qui caractérise l’époque moderne.

Oresme, le plus jeune ami de Philippe de Vitry, le théoricien de la musique, compositeur et évêque de Meaux, est le fondateur de la musicologie moderne. Oresme s’est occupé de presque chaque catégorie de la musicologie (voir Taschow, op. cit.) au sens moderne comme :

• l’acoustique (dans l’Expositio super de anima, Quaestiones de anima, De causis mirabilium, De configurationibus, De commensurabilitate vel incommensurabilitate),
• l’esthétique musicale (dans De configurationibus, De commensurabilitate vel incommensurabilitate),
• la physiologie vocale et auditive (dans les Quaestiones de sensu, Expositio super de anima),
• la psychologie auditive (dans les Quaestiones de anima, De causis mirabilium, Quaestiones de sensu),
• la théorie musicale de la mesure (dans le Tractatus specialis de monocordi, De configurationibus, Algorismus proportionum),
• la théorie de la musique (dans De configurationibus),
• l’exécution musicale (dans De configurationibus),
• la philosophie de musique (dans De commensurabilitate vel incommensurabilitate).

Avec sa théorie très spéciale des espèces (multiplicatio specierum), Oresme a correctement formulé la première théorie de la mécanique ondulatoire du son et de la lumière, trois siècles avant Huygens avec sa description d’un pur transport d’énergie sans propagation matérielle. L’espèce finale au sens où l’entend Oresme signifie les mêmes que le terme moderne de « forme d’onde ».

Oresme a également découvert, trois siècles ans avant Mersenne, le phénomène des tonalités partielles ou « harmoniques » et, quatre siècles et demi avant Joseph Sauveur, la relation entre les traits et la tonalité de couleur. Dans sa « théorie physico-mathématique très détaillée des tonalités et des tonalités de couleur partielles », Oresme a préfiguré la théorie du XIX^e siècle d’Hermann von Helmholtz.

L’esthétique musicale d’Oresme a formulé une « théorie subjective moderne de la perception », qui n’était pas la perception de la beauté objective de la création divine, mais le processus constructif de la perception, qui cause la perception sensible de la beauté ou de la laideur. Par conséquent, on peut voir que chaque individu perçoit un autre « monde ».

Plusieurs des intuitions d’Oresme dans d’autres disciplines comme les mathématiques, la physique, la philosophie, la psychologie, qui annoncent l’image de soi des temps modernes, sont étroitement liées au modèle musical, ce qui est inhabituel dans la pensée actuelle. La Musica fonctionnait comme une sorte d’« ordinateur médiéval » et dans ce sens, représentait un hymne extensif à la nouvelle conscience analytico-quantitative du XIV^e siècle.

Psychologie

Le travail de Taschow a également permis de montrer qu’Oresme était un psychologue exceptionnel. Il a étudié, grâce à l’usage d’une méthode fortement empirique, la complexité de la totalité des phénomènes de la psyché humaine. Oresme avait confiance en l’activité des « sens intérieurs » (sensus interior) et en la constructibilité, la complexité et la subjectivité de l’appréhension du monde. L’usage de ces dispositifs tout à fait progressifs faisait de Oresme un partisan typique de l’École psychologique parisienne de Buridan, Barthélemy de Bruges, Jean de Jandun, Henri de Hesse (Heinrich von Langenstein) etc.) et son travail était étroitement lié aux scientifiques du système optique (Alhazen, Roger Bacon, Vitellion, John Peckham etc.), mais de plus, l’esprit innovateur et hardi d’Oresme a préfiguré des faits très importants de la psychologie des XIX^e et XX^e siècles, particulièrement, dans les domaines de la psychologie cognitive, de la psychologie de la perception, de la psychologie de la conscience et de la psychophysique. Il a découvert l’« inconscient » psychologique et sa grande importance pour la perception et le comportement. Sur cette base, il a formulé, cinq siècles avant Hermann von Helmholtz, sa propre théorie inspirée des « conclusions inconscientes de la perception » et, comme dans les théories du XX^e siècle, son « hypothèse des deux attentions » sur l’attention consciente et inconsciente.

Dans sa « théorie de la connaissance » moderne, Oresme a prouvé qu’aucune pensée, catégorie, limite, qualité ou quantité n’existe hors de la conscience. Il a démasqué, par exemple, les prétendues « qualités primaires » comme la taille, la position, la forme, le mouvement ou le repos, etc. des scientifiques du XVII^e siècle tels que Galilée, Locke etc., qui avaient été considérées comme objectives dans la nature externe, mais qui devaient être vues comme des constructions cognitives très complexes de la psyché dans les différentes conditions individuelles du corps et de l’âme humains. Puisque la réalité n’existe qu’au moment « sans expansion » (instantia), Oresme en a déduit qu’aucun mouvement, excepté dans la conscience, ne pouvait exister. Ceci signifie que le mouvement résulte de la perception humaine et de la mémoire au sens de la composition active de l’« avant » et de l’« après ». Cette théorie sagace devient plausible, par exemple, dans le domaine du son. Oresme a écrit : « s’il existait une créature sans mémoire, celle-ci ne pourrait jamais entendre aucun son…^[6] Le son n’est donc rien de plus qu’une construction humaine.

Dans sa « psycho-cybernétique » et sa « théorie de l’information » modernes, Oresme a résolu le problème du dualisme du monde physique et psychique en employant le schéma des espèces en trois parties «espèce» « matière » « qualité sensible » de sa brillante « théorie de l’espèce » (en termes modernes : information - milieu - signification). L’espèce transportable (information), comme une « forme d’onde » de son, change de milieu (bois, air, eau, système nerveux, etc.) et le sens intérieur (sensus interior) construit, à partir d’elle, une signification subjective au moyen de « conclusions inconscientes ».

Oresme avait déjà développé une première psychophysique qui montre beaucoup de similitudes avec l’approche de Gustav Theodor Fechner, le fondateur de la psychophysique moderne. Les conceptions de la psyché d’Oresme sont fortement mécanistes. Les processus physiques et psychiques sont équivalents en leur structure de mouvement (configuratio qualitatum et motuum). Chaque structure étant dotée d’un moment qualitatif (physique) et quantitatif (psychique), les processus psychologiques (intensités) peuvent en conséquence être mesurés comme les processus physiques. Oresme a ainsi assuré la première légitimation scientifique de la mesure de la psyché et même, contre Aristote et les scolastiques, de l’« âme immatérielle ».

Oresme s’est néanmoins essentiellement concentré sur la psychologie de la perception. il a composé, fait unique au Moyen Âge, un traité spécial sur la perception et son dérangement et l’égarement (De causis mirabilium) dans de nombreuses parties de ses écrits, où il a examiné chaque sens (vue, audition, toucher, odorat, goût) et les fonctions cognitives. Avec la même méthode que celle utilisée par les psychologues du XX^e siècle, à savoir par l’analyse des égarements et des dérangements, Oresme avait déjà identifié beaucoup de lois essentielles de la perception, par exemple les lois figuratives cinq siècles avant Christian von Ehrenfels, les limites (maxima et minima) de perception, etc. (voir Taschow, op. cit.)

Philosophie naturelle

Le travail de Taschow révèle également l’univers très complexe de la pensée philosophique d’Oresme qui a préfiguré beaucoup de vues essentielles de l’image de soi aux temps modernes, telle que son intuition de l’incommensurabilité des proportions normales, de la complexité, de l’indétermination et de l’infinie variabilité du monde, etc. Dans le monde linéairement progressif d’Oresme, tout est unique à chaque fois et, ainsi, il en va également de même pour la connaissance humaine.

L’excellent modèle de ce nouveau monde infini du XIV^e siècle (contrairement aux répétitions sans fin de l’antique musica mundana) résidait dans la machina musica d’Oresme pour qui la musique prouvait de façon analogue qu’avec un nombre limité de proportions et de paramètres, on pourrait produire des structures très complexes, infiniment changeantes et ne se répétant jamais (De configurationibus qualitatum et motuum, De commensurabilitate vel incommensurabilitate, Quaestio contra divinatores). Le message est le même que dans la théorie du chaos du XX^e siècle où l’itération des formules les plus simples produit un monde extrêmement complexe dénué de toute prévisibilité de comportement.

Oresme a fini par créer, à partir des principes musico-mathématiques d’incommensurabilité, d’irrationalité et de complexité, un modèle structurel dynamique pour la constitution des espèces substantielles et des individus de la nature, la théorie dite de perfection des espèces (« perfectio specierum ») (De configurationibus qualitatum et motuum, Quaestiones super de generatione et corruptione, Tractatus de perfectionibus specierum) où l’individu oresmien se transforme, grâce à l’usage d’une analogie des qualités musicales avec les « qualités premières et secondes » d’Empédocle, en système auto-organisé qui prend la peine d’entrer dans son état de système optimal afin de se défendre contre les influences environnementales dérangeantes. Cette « boucle de contrôle automatique » influence la forme substantielle (forma substantialis), déjà présente au sens moderne, dans les principes de l’évolution biologique, l’adaptation et la mutation du matériel génétique.

Il est tout à fait évident que la théorie révolutionnaire d’Oresme dépassait le dogme scolastique aristotélicien des espèces substantielles invariables et préfigurait les principes de la « théorie du système », de l’« auto-organisation » et de l’« évolution biologique » de Darwin.

Une autre approche très progressive d’Oresme était sa recherche extensive sur les valeurs et les mesures statistiques approximatives au moyen de marges d’erreur. Il a formulé sa « théorie des probabilités » dans les domaines de la psychologie, de la physique et des mathématiques. Il a, par exemple, établi deux règles psychologiques (De causis mirabilium), la première règle disant que la probabilité des jugements erronés s’accroît avec l’augmentation du nombre de jugements inconscients de perception (profondeur de la signification) et partant, la probabilité des erreurs de la perception. La deuxième règle dit que plus le nombre de « jugements inconscients » de perception dépasse une limite diffuse^[7] et plus une erreur fondamentale de perception est improbable, parce qu’elle ne décompose jamais la grande majorité des jugements inconscients. La conséquence pour la connaissance théorique de celles-ci selon l’une ou l’autre de ces règles est que la perception n’est rien de plus qu’une valeur de probabilité dans la zone floue de ces deux règles. La perception n’est jamais une « photographie » objective mais une construction complexe sans évidence absolue.

Oresme fournit un exemple de la préfiguration mathématique par des éléments de la stochastique lorsqu’il énonce dans son De proportionibus proportionum : « si nous prenons une multitude finie de nombres entiers positifs, alors c’est le nombre de nombres entiers parfaits ou le nombre de cubes plus inférieurs que d’autres nombres. » En outre, plus nous prenons de nombres et plus la relation des non-cubes aux cubes ou des nombres entiers imparfaits aux nombres entiers est grande. Par conséquent, si nous ne savons pas quelque chose au sujet d’un nombre, il est alors probable (verisimile) que ce nombre n’est pas un cube. C’est comme dans un jeu (sicut est in ludis) où quelqu’un demande si un nombre caché est un cube. Il est plus sûr de répondre « Non » parce que c’est ce qui paraît le plus probable (probabilius et verisimilius). Oresme considérait ensuite une multitude de 100 différents objets mathématiques qu’il avait formés d’une certaine manière et il déterminait qu’à partir de celle-ci, on pouvait former (100 * 99) : 2 = 4950 combinaisons de deux éléments chacun. De ceux-ci, 4925 montrent une certaine qualité intéressante E, tandis que les restants n’ont pas cette qualité E. Finalement, Oresme calculait le quotient 4925 : 25 = 197 : 1 pour en conclure qu’il était probable (verisimile) que, si quelqu’un cherche une combinaison aussi inconnue, celle-ci aura la qualité E. Oresme a ainsi calculé le nombre de cas favorables et défavorables et leurs quotients, mais il n’avait pas encore le quotient du nombre du nombre des favorables et le nombre entier de cas d’égale possibilité. Il ne disposait pas encore de la « mesure de la probabilité » moderne, mais il avait pourtant développé un brillant outil pour juger de la « facilité » à arriver quantitativement à un évènement. Oresme avait recours, dans ses calculs de probabilité, à des termes comme verisimile, probabile / probabilius, improbabile / improbabilius, verisimile / verisimilius / maxime verisimile et possibile equaliter. Personne avant lui, et même longtemps après lui, n’a usé de ces termes dans le contexte des jeux et des probabilités aléatoires. On retrouvera les méthodes d’Oresme plus tard chez Galilée et Pascal au XVII^e siècle.^[8]

Un exemple de l’usage de la théorie des probabilités d’Oresme en physique apparaît dans De commensurabilitate vel incommensurabilitate, De proportionibus proportionum, Ad pauca respicientes etc. lorsque Oresme énonce : « si nous prenons deux grandeurs normales inconnues comme le mouvement, le temps, la distance, etc., il est plus probable (verisimillius et probabilius) que le rapport entre ces deux est irrationnel plutôt que rationnel. Ce théorème qui, selon Oresme, s’applique généralement à la nature tout entière, au monde terrestre et céleste, a un grand effet sur les vues d’Oresme de la nécessité et la contingence, et partant, sur ses vues de la loi naturelle (leges naturae) et sa critique de l’astrologie.

Il est évident que les recherches d’Oresme sur la musique ont inspiré sa théorie des probabilités en physique, mathématiques et psychologie de la perception : la division monocorde (sectio canonis) prouvait le sens de l’audition, et la raison mathématique prouvait clairement que la plupart des divisions de corde produisent des intervalles irrationnels, c’est-à-dire dissonants.

Physique

Les préceptes de physique d’Oresme sont exposés dans deux œuvres en français, le Traité de la sphère, deux fois imprimé à Paris (première édition sans date ; deuxième, 1508) et le Traité du ciel et du monde, rédigé en 1377 à la demande de Charles V, mais jamais imprimé. Dans la plupart des problèmes essentiels de statique et de dynamique, Oresme suit les avis préconisés à Paris par son prédécesseur, Jean Buridan de Béthune et son contemporain Albert de Saxe. Oresme a contré la théorie aristotélicienne du poids qui énonçait que le lieu normal des corps lourds est au centre du monde et que celui des corps légers est dans la concavité du corps rond de la lune, en proposant ce qui suit : « les éléments tendent à se disposer de telle manière que leur poids spécifique diminue par degrés du centre à la périphérie. » Oresme pensait qu’une règle semblable pouvait exister en d’autres mondes que le nôtre. C’est là la doctrine qui a été substituée par la suite à celle d’Aristote par Copernic et ses disciples, tels que Giordano Bruno dont les arguments sont d’ailleurs si semblables à ceux d’Oresme qu’il semblerait qu’il avait lu le Traité du ciel et du monde, mais de droit d’Oresme à être considéré comme le précurseur de Copernic apparaît comme bien plus fermement établi lorsqu’on considère ce qu’il dit du mouvement journalier de la terre, sur lequel il a glosé dans les chapitres XXIV et XXV du Traité du ciel et du monde. Il commence par établir qu’aucune expérience ne peut décider si les cieux se déplacent d’est en ouest ou si la terre se déplace d’ouest en est dans la mesure où l’expérience sensible ne peut jamais établir plus d’un mouvement relatif. Il a ensuite prouvé que les raisons proposées par la physique aristotélicienne contre le mouvement de la terre étaient irrecevables. Oresme a précisé, en particulier, le principe de la solution de la difficulté tirée du mouvement des projectiles. Il a ensuite établi des règles d’interprétation pour résoudre les objections fondées sur des passages du texte biblique qui sont encore universellement suivies par les exégètes catholiques actuels. En conclusion, il soutient la théorie du mouvement de la terre et non des cieux grâce à l’argument de la simplicité, et la totalité de son argument en faveur du mouvement de la terre est à la fois plus explicite et beaucoup plus clair que celui qu’en a donné Copernic.

Il n'est pas surprenant que, s’occupant de questions de mécanique ondulatoire, du son et de la lumière, Oresme ait été le premier à théoriser que la nature de la couleur et de la lumière sont identiques. Il avait tout à fait raison de supposer que la couleur n’est que de la lumière blanche brisée et reflétée, c’est-à-dire que « les couleurs font partie de la lumière blanche ». Cette brillante théorie a en outre été inspirée par ses investigations musicologiques : dans sa théorie des harmoniques et de la couleur de tonalité, il a établi une analogie entre ces faits musicaux et le phénomène du mélange de couleurs sur un tour.^[9]

Enfin, il y a la découverte géniale d’Oresme de la courbe de la lumière par réfraction atmosphérique : dans son traité De visione stellarum, il demande si les étoiles sont réellement là où elles paraissent être. L’usage de l’optique lui a permis de répondre par la négative. Deux siècles avant la révolution scientifique, Oresme a proposé la solution qualitativement correcte au problème de la réfraction atmosphérique, à savoir que la lumière voyage le long d’une courbe par un milieu de densité uniformément variable. Oresme est arrivé à cette solution en se servant des infinitésimales pour jeter le doute sur toutes les données sensibles visuelles en concluant que presque rien dans les cieux ou sur terre n’est vraiment là où on le voit. Cette solution qui avait échappé à Ptolémée et à Alhazen avait même échappé à Kepler au XVII^e siècle et jusqu’à présent, c’est Hooke qui a été crédité pour sa découverte et Newton pour sa résolution mathématique.

Ces fragments de l’œuvre monumentale d’Oresme montrent qu’il était l’un des scientifiques les plus innovateurs à l’aube de l’âge moderne et un pionnier du monde moderne.

Notes

Œuvres

• Traité des monnaies et autres écrits monétaires du XIV^e siècle (Jean Buridan, Bartole de Sassoferrato), Claude Dupuy, Frédéric Chartrain, Lyon, La Manufacture, 1989
• Expositio et quaestiones in Aristotelis De anima, Éd. Benoît Patar, Louvain, Éd. Peeters, 1995
• Le livre de politiques d'Aristote, Albert D. Menut, Philadelphia, American Philosophical Society, 1970
• Le livre du ciel et du monde ; texte et commentaire, Éd. Albert D. Menut, Alexandre Joseph Denomy, New York, London, 1941-1943
• Quaestiones super geometriam Euclidis, Éd. H. L. L. Busard, Leiden, E.J. Brill, 1961
• Tractatvs de origine et natura, iure & mutationibus monetarvm, Düsseldorf : Verlag Wirtschaft und Finanzen, 1995, 1485
• Traictie de la première invention des monnoies de Nicole oresme textes français et latin d'après les manuscrits de la Bibliothèque impériale et Traité de la monnoie de Copernic, texte latin et traduction française, Paris, Guillaumin, 1864, Genève, Slatkine Reprints, 1976
• Traité de l'espere, McCarthy, Lillian, 1943, 1974
• Traité des monnaies et autres écrits monétaires du XIV^e siècle (Jean Buridan, Bartole de Sassoferrato) : textes, Claude Dupuy et al., Lyon, La Manufacture; 1989
• Messire Frãçois Petracque des remedes de lune [et] autre fortune, prospere [et] aduerse, Paris, Denis Ianot, 1534, 1523

Références

• Pierre Maurice Marie Duhem, Un précurseur français de Copernic : Nicole Oresme (1377), Paris, Librairie Armand Colin, 1909
• Francis Meunier, Essai sur la vie et les ouvrages de Nicole Oresme, Paris, Ch. Lahure, 1857
• Pierre Souffrin, Alain-Philippe Segonds, Nicolas Oresme : tradition et innovation chez un intellectuel du XIV^e siècle, Paris, Les Belles Lettres, 1988 (Science et humanisme). ISBN 2-251-34505-1.
• (de)Ulrich Taschow, Nicole Oresme und der Frühling der Moderne: Die Ursprünge unserer modernen quantitativ-metrischen Weltaneignungsstrategien und neuzeitlichen Bewusstseins- und Wissenschaftskultur, Avox Medien Verlag, 2003 ISBN 3936979006

Bibliographie

• Charles-Ernest de Fréville de Lorme, Mémoire sur la cosmographie du Moyen Âge, le Traité de la sphère par Nicolas Oresme et les découvertes maritimes des Normands, Paris, P. Dupont, 1860
• Nicolas Oresme, Traictié de la première invention des monnoies (précédé d'une étude), éd. Louis Wolowski, Paris, 1864
• Adolphe Landry, Notes critiques sur le Nicole Oresme de M. Bridrey, Paris, Champion, 1909
• Autour de Nicole Oresme : actes du Colloque Oresme, Éd. Jeannine Quillet, Colloque Oresme Université de Paris XII, 1987, Paris, J. Vrin, 1990 ISBN 2711610179
• Edouard Lévy, Le statut de la monnaie chez Jean Buridan et Nicole Oresme, Paris, Mémoire de DEA, 1991
• Émile Bridrey, Nicole Oresme : étude d'histoire des doctrines et des faits économiques : la théorie de la monnaie au XIV^e siècle, Genève, Slatkine, 1978, 1906
• Henry Hertrich, Les théories monétaires au XIV^e siècle : Nicolas Oresme, Lyon, Legendre, 1899
• Jacqueline Fau, Jeanne-Marie Viel, Nicole Oresme, Traité monétaire Treatise on money (1355), Édition trilingue juxtaposée Latinus-Français-English, Paris, Editions Cujas, 1990
• Jan Pieter Hubert Knops, Études sur la traduction française de la morale à Nicomache d'Aristote par Nicole Oresme, 's-Gravenhage, Excelsior,1953
• Léopold Delisle, Observations sur plusieurs manuscrits de la politique et de l'économique de Nicole Oresme, Nogent-le-Rotrou, A. Gouverneur, 1870-1879
• Sylvain Piron, Nicolas Oresme : violence, langage et raison politique, Florence, European University Institute, Dept. of History and Civilisation, 1997.

Liens externes

• Alain Costé, L’œuvre scientifique de Nicole Oresme, Université de Caen, Laboratoire de Mathématiques Nicolas Oresme, 1997
• Bibliographie extensive de Nicole Oresme
• Octave Encoignard, Nicole Oresme, Grand Maître du Collège de Navarre, Évêque de Lisieux, 1902.
• Article sur la théorie monétaire de Nicole Oresme

• Portail du Moyen Âge tardif
• Portail de l’astronomie
• Portail des mathématiques