- Liste de fractales par dimension de hausdorff
-
Liste de fractales par dimension de Hausdorff
Cet article est une liste de fractales, ordonnées par dimension de Hausdorff croissante.
En mathématiques, une fractale est un ensemble dont la dimension de Hausdorff (notée δ) est strictement supérieure à la dimension topologique[1].
Sommaire
Fractales déterministes
δ < 1
δ
(val. exacte)δ
(val. approchée)Nom Illustration Remarques 0 ⇒ donc pas une fractale mais dim box-counting = 1 0 Nombres rationnels La dimension de Hausdorff des ensembles dénombrables vaut toujours zéro. Ces ensembles ne peuvent être fractals. Ajoutons que la dimension "box counting" d'un tel ensemble peut être différent s'il s'agit d'un sous-ensemble dense d'une région ouverte de R. L'ensemble des nombres rationnels a ainsi une dimension box-counting de "1" car sa clôture est R[1]. Calculé 0.538 Attracteur de Feigenbaum 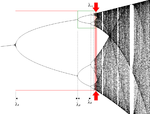
L'attracteur de Feigenbaum (entre les flèches) est l'ensemble des points générés par itérations successives de la fonction logistique pour le paramètre critique 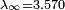 , où le doublement de périodes est infini. Remarque : cette dimension est la même pour toute fonction différentiable et unimodale[2].
, où le doublement de périodes est infini. Remarque : cette dimension est la même pour toute fonction différentiable et unimodale[2].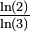
0,6309 Ensemble de Cantor 
Construit en retirant le tiers central à chaque itération. Nulle part dense et de mesure nulle mais indénombrable. 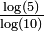
0.69897 Nombres réels avec décimales paires 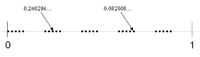
Similaire à un ensemble de Cantor[1]. 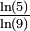
0,7325 Fractale UNU 
Fractale auto-descriptive construite par itérations successives du schéma suivant : u → unu (un « u ») → unuunnunu (un « u », un « n », un « u ») → etc. 1 ≤ δ < 2
δ
(val. exacte)δ
(val. approchée)Nom Illustration Remarques 1 1.0000 Ensemble de Smith-Volterra-Cantor 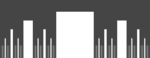
Construit en retirant le quart, puis le seizième, le 64e… central à chaque itération. N'est nulle part dense mais est indénombrable et a pour mesure de Lebesgue 1/2. Il a donc pour dimension 1. 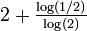
1.0000 Courbe de Takagi ou Blancmange 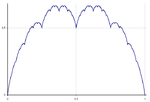
Définie sur l'intervalle unité par 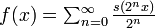 , où s(x) est la fonction "dents de scie". Cas particulier de la courbe de Takahi-Landsberg:
, où s(x) est la fonction "dents de scie". Cas particulier de la courbe de Takahi-Landsberg: 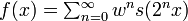 avec
avec 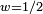 . La dimension de Hausdorff vaut 2 + log(w) / log(2). (Hunt cité par Mandelbrot [3] ).
. La dimension de Hausdorff vaut 2 + log(w) / log(2). (Hunt cité par Mandelbrot [3] ).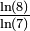
1,0686 Île de Gosper 
calculé 1.0812 Ensemble de Julia z² + 1/4 
Ensemble de Julia pour c = 1/4[4]. Solution s de 2 | α | 3s + | α | 4s = 1 1.0933 Frontière de la Fractale de Rauzy 
Représentation géométrique du système dynamique associé à la substitution de Tribonacci: 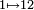 ,
, 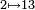 et
et 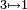 [5]..α est l'une des deux racines complexes conjuguées de z3 − z2 − z − 1 = 0.
[5]..α est l'une des deux racines complexes conjuguées de z3 − z2 − z − 1 = 0.Mesuré(Box counting) 1.2 Ensemble de Julia "Dendrite" 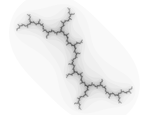
Ensemble de Julia pour c=i 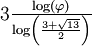
1.2083 Fractale du mot de Fibonacci à 60 ° 
Construit à partir du Mot de Fibonacci, avec un angle à 60°. Voir aussi la fractale du mot de Fibonacci standard, ci-dessous [6]. Avec 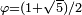 (Nombre d'or).
(Nombre d'or).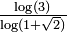
1.2465 Frontière de la fractale du mot de Fibonacci 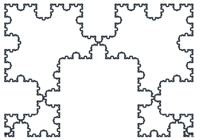
Construite à partir du Mot de Fibonacci. Voir aussi la fractale du mot de Fibonacci standard, ci-dessous [6]. Avec 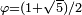 (Nombre d'or).
(Nombre d'or).1,26 Attracteur de Hénon 
La carte de Hénon canonique (a = 1,4 et b = 0.3) possède δ = 1,261 ± 0,003. Différents paramètres conduisent à différentes valeurs de δ 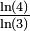
1,2619 Courbe de Koch 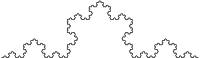
En juxtaposant 3 fois cette courbe en triangle on obtient le flocon de Koch et l'anti-flocon de Koch si elle est inversée. 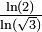
1,2619 Frontière de la Courbe Terdragon, Fudgeflake 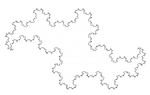
L-System : similaire à la courbe du dragon avec un angle de 30°. Le Fudgeflake est construit en juxtaposant 3 segments initiaux en triangle. 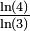
1,2619 Carré de Cantor 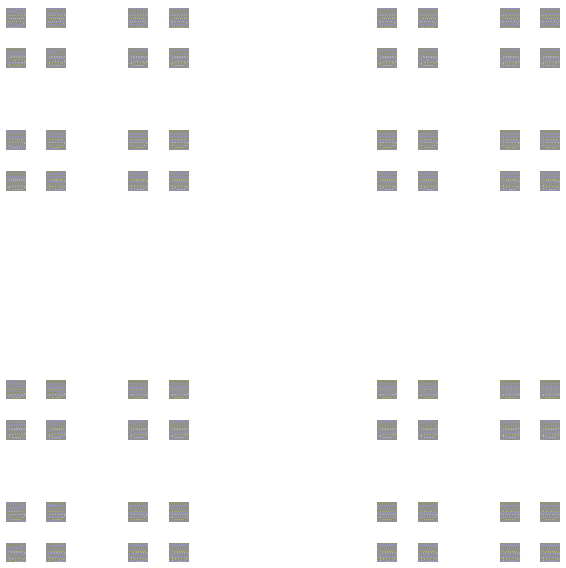
Ensemble de Cantor en deux dimensions. calculé 1,2683 Ensemble de Julia pour z²-1 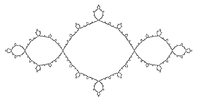
Ensemble de Julia pour c=-1[7]. calculé 1,3 Fractale Beryl pour k=1 
Pour k=1. La fractale Béryl est définie par f(x, y)→(k(x+y), xy) avec x et y complexes et la coupe dans le plan ν0 = 1[8] calculé 1,3057 Baderne d'Apollonius 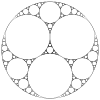
Voir [9] calculé (box-counting) 1.328 Fractale d'inversion à 5 cercles 
L'ensemble limite généré itérativement via des inversions par rapport à 5 cercles tangents. Également une baderne d'Apollonius à 4 cercles de base. Voir [10] calculé 1.3934 Lapin de Douady 
Ensemble de Julia pour c=-0,123+0.745i[11]. mesuré (box counting) 1,42 +/- 0,02 Fractale de Newton 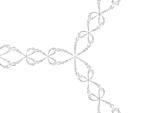
Frontière triple des bassins d'attraction des 3 racines complexes de l'equation z3 − 1 = 0 par la méthode de Newton. 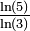
1,4649 Fractale de Vicsek 
Construit en substituant itérativement chaque carré par une croix de 5 carrés. 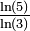
1,4649 Courbe de Koch quadratique (type 1) 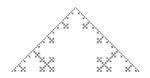
On y retrouve le motif de la fractale box (voir ci-dessus), construit différemment. 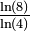
1,5000 Courbe de Koch quadratique (type 2) 
Appelée également « saucisse de Minkowski ». 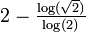 (supposé exact)
(supposé exact)1.5000 une fonction de Weierstrass: 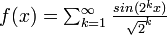
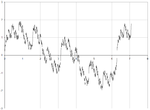
La dimension de Hausdorff de la fonction de Weierstrass ![\scriptstyle{f : [0,1] \to \mathbb{R}}](/pictures/frwiki/48/0a248566ccd0c470073e1ce95e8f32e6.png) définie par
définie par 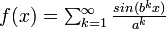 avec 1 < a < 2 et b > 1 a pour borne supérieure
avec 1 < a < 2 et b > 1 a pour borne supérieure 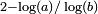 . Il est conjecturé qu'il s'agit de la valeur exacte. Le même résultat peut être établi en utilisant, à la place de la fonction sinus, d'autres fonctions périodiques comme cosinus[1].
. Il est conjecturé qu'il s'agit de la valeur exacte. Le même résultat peut être établi en utilisant, à la place de la fonction sinus, d'autres fonctions périodiques comme cosinus[1].1,5236 Frontière courbe du dragon 
Cf. Chang & Zhang[12]. 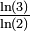
1,5850 Arbre à trois branches 
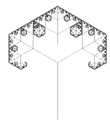
Chaque branche porte trois branches (ici 90 ° et 60°). La dimension fractale de l'arbre est celle des branches terminales. 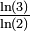
1,5850 Triangle de Sierpiński C'est également le triangle de Pascal modulo 2. 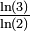
1,5850 Courbe de Sierpiński en pointe de flèche 
Même limite que le triangle de Sierpiński (ci-dessus), mais obtenue par itérations d'une courbe unidimensionnelle. 1 + log3(2) 1,6309 Triangle de Pascal modulo 3 
D'une manière générale pour un triangle modulo k, si k est premier, la dimension fractale est 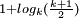 (Cf.Stephen Wolfram[13])
(Cf.Stephen Wolfram[13])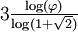
1,6379 Fractale du mot de Fibonacci 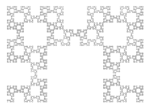
Fractale basée sur le mot de Fibonacci (ou séquence du Lapin) Sloane A005614. Illustration : Fractale après F23 = 28657 segments[6].. Avec 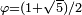 (Nombre d'or).
(Nombre d'or).Solution de 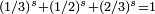
1.6402 Attracteur d'un IFS avec 3 similitudes de ratios 1/3, 1/2 and 2/3 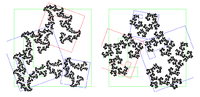
Generalisation : Supposant la condition d'ensemble ouvert satisfaite, l'attracteur d'un système de fonctions itérées à n simulitudes de ratio cn, a pour dimension de Hausdorff s, solution de l'équation : 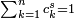 [1].
[1].1 + log5(3) 1,6826 Triangle de Pascal modulo 5 
D'une manière générale pour un triangle modulo k, si k est premier, la dimension fractale est 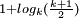 (Cf.Stephen Wolfram[13])
(Cf.Stephen Wolfram[13])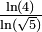
1,7227 Fractale Pinwheel 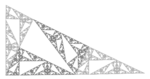
Construite à partir du pavage "pinwheel" de John Conway. 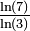
1,7712 Flocon hexagonal 
Construit en substituant itérativement chaque hexagone par un flocon de 7 hexagones. Sa frontière est le flocon de Koch. Contient une infinité de flocons de Koch (en positif comme en négatif). 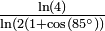
1,7848 Courbe de Koch à 85 °, fractale de Cesàro 
Généralisation de la courbe de Koch basée sur un angle a choisi entre 0 et 90°. La dimension fractale vaut alors 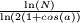 . La fractale de Cesàro est basée sur ce motif.
. La fractale de Cesàro est basée sur ce motif.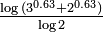
1.8272 Une fractale auto-affine 
Construite itérativement à partir d'une grille 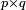 sur un carré, avec
sur un carré, avec 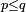 . Sa dimension de Hausdorff égale
. Sa dimension de Hausdorff égale 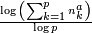 [1] avec
[1] avec 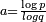 et nk le nombre d'éléments dans la colonne k. La Dimension de Minkowski–Bouligand (box counting) donne une formule différente, donc une valeur souvent différente. Contrairement aux fractales auto-similaires, la dimension de Hausdorff des fractales auto-affines dépend de la position des éléments itérés et il n'existe pas de formule simple pour le cas général.
et nk le nombre d'éléments dans la colonne k. La Dimension de Minkowski–Bouligand (box counting) donne une formule différente, donc une valeur souvent différente. Contrairement aux fractales auto-similaires, la dimension de Hausdorff des fractales auto-affines dépend de la position des éléments itérés et il n'existe pas de formule simple pour le cas général.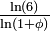
1,8617 Flocon pentagonal (pentaflake) 
Construit en substituant itérativement chaque pentagone par un flocon de 6 pentagones. Ici, φ est le nombre d'or et vaut 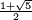
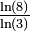
1,8928 Tapis de Sierpiński 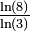
1,8928 Cube de Cantor 
Ensemble de Cantor en trois dimensions. Estimé 1,9340 Frontière de la fractale de Lévy 
Estimé par Duvall et Keesling (1999). La fractale de Lévy en elle-même a pour dimension de Hausdorff 2. 1,974 Pavage de Penrose 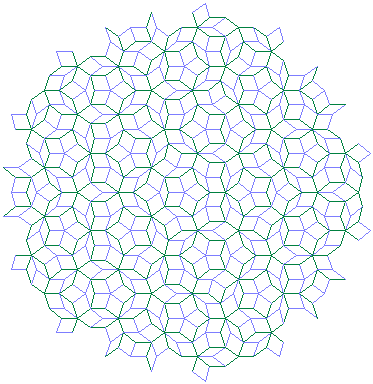
Cf. Ramachandrarao, Sinha & Sanyal[14] δ = 2
δ
(val. exacte)δ
(val. approchée)Nom Illustration Remarques 2 2 Frontière de l'ensemble de Mandelbrot 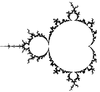
La frontière a la même dimension que l'ensemble[15].. 2 2 certains ensembles de Julia 
Pour des valeurs de c déterminées (sur la frontière de l'ensemble de Mandelbrot), l'ensemble de Julia a pour dimension 2[16].. 2 2 Courbe de Sierpiński 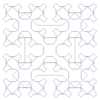
Toute courbe remplissant l'espace possède une dimension de Hausdorff δ = 2. 2 2 Courbe de Hilbert 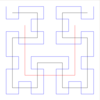
Peut être étendue à trois dimensions. 2 2 Courbe de Peano 
et une famille de courbes de construction similaire, dont les courbes de Wunderlich. 2 2 Courbe de Moore 
Peut être étendue à 3 dimensions. 2 2 Courbe de Lebesgue 
Contrairement aux courbes ci-dessus, celle-ci est presque partout différentiable. Un deuxième type de courbe 2D a également été défini. Cette courbe peut être étendue en 3D avec une dimension fractale de 3[17].. 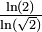
2 Courbe du dragon 
Sa frontière a une dimension fractale de 1,5236 (Cf.Chang & Zhang[12]) 2 Courbe "Terdragon" 
L-System : F→ F+F-F ; angle=120°. 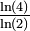
2 T-square 
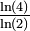
2 Courbe de Peano-Gosper 
Sa frontière est l'île de Gosper. 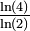
2 Tétraèdre de Sierpiński 
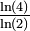
2 Fractale H 
Également, l'arbre de Mandelbrot, qui a une structure similaire. 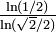
2 Arbre de Pythagore 
Chaque carré génère deux carrés de côté réduit de racine(2)/2. 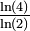
2 Fractale en croix grecque 
Chaque segment est substitué par une croix formée de quatre segments. 2 < δ < 3
δ
(val. exacte)δ
(val. approchée)Nom Illustration Remarques 2,06 Attracteur étrange de Lorenz 
Pour les paramètres de l'attracteur: v=40,σ=16 et b=4[18]. 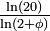
2,3296 Dodécaèdre fractal 
Chaque dodécaèdre est substitué par 20 dodécaèdres. 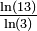
2,33 Surface quadratique de Koch en trois dimensions de type 1 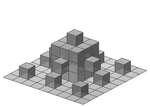
Extension en trois dimensions de la courbe quadratique de Koch en deux dimensions de type 1 (la figure illustre la deuxième itération). 2,47 Interstices des sphères apolloniennes 
Baderne d'Apollonius en trois dimensions. Modélise la mie de pain ou l'éponge. Dimension calculée par M. Borkovec, W. De Paris et R. Peikert[19]. 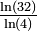
2,50 Surface quadratique de Koch en trois dimensions de type 2 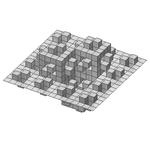
Extension en trois dimensions de la courbe quadratique de Koch en deux dimensions de type 2 (la figure illustre la deuxième itération). 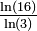
2,5237 Hypercube de Cantor pas de représentation possible Ensemble de Cantor en 4 dimensions. D'une manière générale, dans un espace de dimension n, l'ensemble de Cantor a une dimension fractale égale à 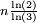
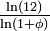
2,5819 Icosaèdre fractal 
Chaque icosaèdre est substitué par 12 icosaèdres. 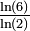
2,5849 Octaèdre fractal 
Chaque octaèdre est substitué par 6 octaèdres. 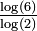
2.5849 Surface de Koch 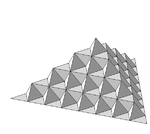
Chaque triangle équilatéral est remplacé par 6 triangles deux fois plus petits. Extension en 2 dimensions de la courbe de Koch. 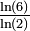
2,59 Fractale en croix grecque en trois dimensions 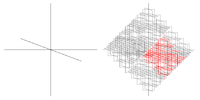
Chaque segment est substitué par une croix en trois dimensions formée de 6 segments. Extension en trois dimensions de la croix en deux dimensions. 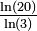
2,7268 Éponge de Menger 
Sa surface a une dimension fractale de 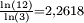 .
.δ = 3
δ
(val. exacte)δ
(val. approchée)Nom Illustration Remarques 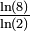
3 Courbe de Hilbert en trois dimensions 
Courbe de Hilbert étendue à trois dimensions 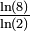
3 Courbe de Lebesgue en trois dimensions 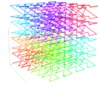
Courbe de Lebesgue étendue à trois dimensions[20].. 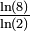
3 Courbe de Moore en trois dimensions 
Courbe de Moore étendue à trois dimensions. Fractales aléatoires et naturelles
δ
(val. exacte)δ
(val. approchée)Nom Illustration Remarques Solution de 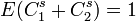 avec E(C1) = 0,5 et E(C2) = 0,3
avec E(C1) = 0,5 et E(C2) = 0,30.7499 Ensemble de Cantor aléatoire 50% / 30% 
A chaque itération, la longueur de l'intervalle de gauche est définie par une variable aléatoire C1: un pourcentage variable de la longueur du segment d'origine. Idem pour l'intervalle de droite, avec pour autre variable aléatoire C2. Sa dimension de Hausdorff s satisfait alors l'équation : 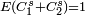 . (E(X) est l'espérance mathématique de X)[1].
. (E(X) est l'espérance mathématique de X)[1].Mesuré 1,05 Chromosome humain no 22 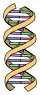
Voir référence pour les détails de la méthode de calcul [21]. Solution de s + 1 = 12 * 2 − (s + 1) − 6 * 3 − (s + 1) 1.144… Courbe de Koch avec intervalle aléatoire 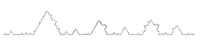
La longueur de l'intervalle médian est une variable aléatoire à distribution uniforme dans (0;1/3)[1]. mesuré 1,24 Côte de Grande-Bretagne 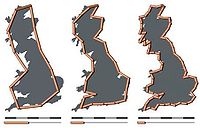
Dimension fractale de la côte ouest de Grande-Bretagne, mesurée par Lewis Fry Richardson et cité par Benoît Mandelbrot[22]. 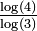
1.2619 Courbe de Koch avec orientation aléatoire 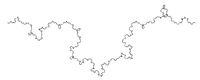
On introduit ici un élément de hasard qui n'affecte pas la dimension en choisissant aléatoirement, à chaque itération, de placer le triangle équilatéral au-dessus ou en dessous de la courbe[1]. 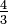
1,33 Frontière du mouvement brownien[23] 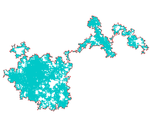
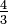
1,33 Polymère en deux dimensions Similaire au mouvement brownien sans auto-intersection[24]. 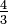
1,33 Front de percolation, front de corrosion en deux dimensions 
Dimension fractale du front de percolation par invasion au seuil de percolation (59,3%). C'est également la dimension fractale du front de corrosion[24]. 1,40 Agrégat d'agrégats en deux dimensions Des agrégats se combinent progressivement en un agrégat unique de dimension 1,4[24]. 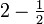
1.5 Graphe d'une fonction Brownienne 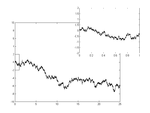
Graphe d'une fonction f telle que, pour tout couple de réels positifs x et x + h, la différence de leurs images f(x + h) − f(x) suit une distribution gaussienne centrée de variance = h. Généralisation : Une fonction fractionnelle Brownienne d'index α suit la même définition mais avec une variance = h2α, dans ce cas, la dimension de Hausdorff de son graphe = 2 − α[1]. Mesuré 1,52 Côte de Norvège 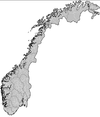
Cf J. Feder [25]. Mesuré 1,55 Marche aléatoire sans intersection 
Marche aléatoire dans un réseau carré sans auto-intersection, avec algorithme de retour arrière pour évitement des impasses. 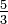
1,66 Polymère en trois dimensions Similaire au mouvement brownien dans un réseau cubique, mais sans auto-intersection[24]. 1,70 Agrégat par diffusion en deux dimensions 
En deux dimensions, des particules forment progressivement par diffusion un agrégat de dimension 1,70[24]. 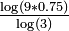
1.7381 Percolation fractale à 75% de probabilité 
Le modèle de percolation fractale est construit par le remplacement progressif de chaque carré par une grille de 3x3 dans laquelle est placée une collection aléatoire de sous-carrés, chaque sous-carré ayant une probabilité p d'être retenu. La dimension de Hausdorff "presque certaine" égale 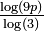 [1].
[1].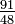
1,8958 Amas de percolation en deux dimensions 
Sous le seuil de percolation (59,3%), l'amas de percolation par invasion couvre une surface de dimension fractale 91/48[24]. Au delà du seuil, l'amas est infini et 91/48 devient la dimension fractale des « clairières ». 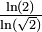
2 Mouvement brownien 
Modélisé par la marche aléatoire. La dimension de Hausdorff reste égale 2 dans toutes les dimensions supérieures ou égales à 2. Mesuré Environ 2 Distribution des amas de galaxies 
Mesuré à partir des résultats 2005 du Sloan Digital Sky Survey. Voir référence [26] 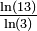
2,33 Surface du chou-fleur 
Chaque branche porte environ 13 branches 3 fois plus courtes. 2,4 ± 0,2 Boule de papier froissé 
Le diamètre de la boule de papier froissé, élevé à une puissance non entière comprise entre 2 et 3 est approximativement proportionnel à la surface de papier utilisé[27]. Les plis se forment à toutes les échelles. 2,50 Agrégat par diffusion en trois dimensions 
En trois dimensions, des particules forment progressivement par diffusion un agrégat de dimension 2,5[24]. 2.50 Figure de Lichtenberg 
Les décharges electriques arborescentes, dites figures de Lichtenberg, croissent à la manière d'une diffusion par agrégation [24]. 
2.5 surface Brownienne 
Une fonction Erreur math (erreur lexicale): \scriptstyle{f:\mathbb{R}^2 → \mathbb{R}} , donne l'altitude d'un point (x,y) telle que, pour deux incréments positifs h et k,
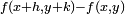 suive une distribution Gaussienne centrée de variance =
suive une distribution Gaussienne centrée de variance = 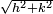 . Généralisation : Une surface Brownienne fractionnelle d'index α suit la même définition mais avec une variance =
. Généralisation : Une surface Brownienne fractionnelle d'index α suit la même définition mais avec une variance = 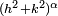 , dans ce cas, sa dimension de Hausdorff = 3 − α[1].
, dans ce cas, sa dimension de Hausdorff = 3 − α[1].Mesuré 2.66 Brocoli[28] 
2.79 Surface du cerveau humain[29] 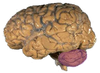
2,97 Surface pulmonaire 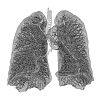
Le réseau d'alvéoles pulmonaires forme une surface fractale proche de 3[24]. Calculé 3 Corde quantique 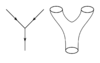
Trajectoire d'une corde quantique dont le point représentatif dérive au hasard[30]. Voir aussi
Références
- ↑ a , b , c , d , e , f , g , h , i , j , k et l (en) Kenneth Falconer, Fractal Geometry: Mathematical Foundations and Applications, John Wiley & Sons, Ltd., 2003 (ISBN 0-470-84862-6), p. xxv
- ↑ Dimension fractale de l'attracteur de Feigenbaum
- ↑ (en) Benoit Mandelbrot, Gaussian self-affinity and Fractals (ISBN 0-387-98993-5)
- ↑ Dimension fractale de l'ensemble de Julia pour c = 1/4
- ↑ Frontière du fractal de Rauzy
- ↑ a , b et c Dimension fractale de la fractale du mot de Fibonacci
- ↑ Dimension fractale de l'ensemble de Julia z²-1
- ↑ Dimension fractale de la fractale Béryl pour k=1
- ↑ Dimension fractale de la baderne d'Apollonius
- ↑ Dimension de la fractale d'inversion à 5 cercles
- ↑ Dimension fractale du lapin de Douady
- ↑ a et b Dimension fractale de la courbe du dragon
- ↑ a et b Stephen Wolfram, Geometry of Binomial Coefficients (1984)
- ↑ P. Ramachandrarao, A. Sinha et D. Sanyal, On the fractal nature of Penrose tiling [1] [pdf]
- ↑ Dimension fractale de la la frontière de l'ensemble de Mandelbrot
- ↑ Dimension fractale de la frontière de certains ensembles de Julia
- ↑ Variantes 2D et 3D de la courbe de Lebesgue
- ↑ The fractal dimension of the Lorenz attractor, Mc Guinness (1983)
- ↑ M. Borkovec, W. De Paris et R. Peikert, The Fractal Dimension of the Apollonian Sphere Packing [2] [pdf]
- ↑ Extension 3D de la courbe de Lebesgue
- ↑ Dimension fractale du chromosome humain n°22
- ↑ How long is the coast of Britain? Statistical self-similarity and fractional dimension, B. Mandelbrot
- ↑ Gregory F. Lawler, Oded Schramm, Wendelin Werner (2000). "The Dimension of the Planar Brownian Frontier is 4/3." 2.
- ↑ a , b , c , d , e , f , g , h et i Bernard Sapoval, Universalités et fractales, Flammarion, coll. « Champs », 2001 (ISBN 2-080-81466-4)
- ↑ Feder, J., "Fractals,", Plenum Press, New York, (1988)
- ↑ Basic properties of galaxy clustering in the light of recent results from the Sloan Digital Sky Survey
- ↑ (it) Filipponi, Introduzione alla fisica, 2005 (ISBN 8-808-07073-5)
- ↑ (en) Glenn Elert, « Fractal Dimension of Broccoli », The Physics Factbook. Consulté le 5 avril 2007
- ↑ Frank Grünberg, « Der Vater des Apfelmännchens », 2005, Technology Review. Consulté le 5 avril 2007
- ↑ Dimension de Hausdorff d'une corde quantique
Bibliographie
- Kenneth Falconer, Fractal Geometry, John Wiley & Son Ltd (mars 1990), (ISBN 0471922870)
- Benoît Mandelbrot, The Fractal Geometry of Nature, W. H. Freeman & Co (septembre 1982), (ISBN 0716711869) .
- Heinz-Otto Peitgen, The Science of Fractal Images, Dietmar Saupe (éditeur), Springer Verlag (août 1988), (ISBN 0387966080)
- Michael F. Barnsley, Fractals Everywhere, Morgan Kaufmann; (ISBN 0120790610)
- Bernard Sapoval, Universalités et fractales, , Flammarion, collection Champs (2001), (ISBN 2080814664)
Liens internes
- Benoît Mandelbrot (biographie, et historique de sa découverte)
- Art fractal
- Théorie constructale
- Compression fractale
- Fractale
- Xaos
Liens externes
Catégorie chaos et fractales de l’annuaire dmoz
- Les fractales sur Mathworld
- D'autres exemples sur le site de Paul Bourke
- La Galerie de Soler
- La rubrique "fractales" de mathcurve.com
- Les archives des Fractale ont édité sur le USENET
- 1000fractales.free.fr - Projet rassemblant des fractales réalisées avec différents logiciels
- Calcul de la dimension fractale de la frontière du dragon
- Calcul de la dimension fractale du pavage de Penrose
- Calcul de la dimension fractale du triangle de Pascal modulo k
- Calcul de la dimension fractale de l'interstice des sphères apolloniennes
- Portail de la géométrie
Catégorie : Fractale
Wikimedia Foundation. 2010.



