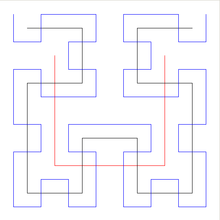
- Courbe de Hilbert
-
Courbe de Hilbert, première itération
Courbe de Hilbert, deuxième itération
Courbe de Hilbert, troisième itération
Courbe de Hilbert en trois dimensions.La courbe de Hilbert est une courbe fractale continue remplissant le plan. Elle a été décrite pour la première fois par le mathématicien allemand David Hilbert en 1891[1]¨.
Comme elle couvre un plan, sa dimension de Hausdorff (à la limite
) est 2.
La longueur euclidienne de Hn est
, elle croit exponentiellement avec n.Pour les bases de données multi-dimensionnelles, la courbe de Hilbert a été proposée à la place de la Courbe de Lebesgue (en) parce qu'elle a un comportement préservant mieux la localité.
Sommaire
Démonstration de la surjection du plan
On peut définir la fonction limite simple
![f : [0;1] \longrightarrow [0;1]^2](f/70f8d4f16f680286054b0329c19c9155.png)
des courbes ![f_n : [0;1] \longrightarrow [0;1]^2](c/f1cde1c6bdef35d28ec89266722a45fb.png)
définies précédemment.On montre facilement que cette fonction est en fait limite uniforme des fonctions fn. Cela tient essentiellement à la localité des courbes de Hilbert.
f, en tant que limite uniforme de fonctions continues, est continue.
Comme toute fonction continue, l'image du compact [0;1] par f est un compact. Notamment, c'est un fermé. Par aillleurs, f([0;1]) est dense dans [0;1]2. C'est donc [0;1]2 tout entier.
Representation en L-Système
La courbe de Hilbert peut être construite par un L-système
- Alphabet : L, R
- Constantes : F, +, −
- Axiome : L
- Règles:
- L → +RF−LFL−FR+
- R → −LF+RFR+FL−
Ici, F signifie "avance", + signifie "à gauche 90°", et - signifie "à droite 90°"
Programme
Butz[2] propose un algorithme pour calculer la courbe de Hilbert en plusieurs dimensions.
Le programme Java suivant trace une courbe de Hilbert par quatre méthodes qui s'appellent récursivement :
import java.awt.*; import java.applet.*; public class HilbertCurve extends Applet { private SimpleGraphics sg=null; private int dist0=512, dist=dist0; public void init() { dist0 = 512; resize ( dist0, dist0 ); sg = new SimpleGraphics(getGraphics()); } public void paint(Graphics g) { int level=4; dist=dist0; for (int i=level;i>0;i--) dist /= 2; sg.goToXY ( dist/2, dist/2 ); HilbertU(level); // start recursion } // Trace courbe "U" à cette échelle: private void HilbertU(int level) { if (level > 0) { HilbertD(level-1); sg.lineRel(0,dist); HilbertU(level-1); sg.lineRel(dist,0); HilbertU(level-1); sg.lineRel(0,-dist); HilbertC(level-1); } } // Trace courbe "]" à cette échelle: private void HilbertD(int level) { if (level > 0) { HilbertU(level-1); sg.lineRel(dist,0); HilbertD(level-1); sg.lineRel(0,dist); HilbertD(level-1); sg.lineRel(-dist,0); HilbertA(level-1); } } // Trace courbe "[" à cette échelle: private void HilbertC (int level) { if (level > 0) { HilbertA(level-1); sg.lineRel(-dist,0); HilbertC(level-1); sg.lineRel(0,-dist); HilbertC(level-1); sg.lineRel(dist,0); HilbertU(level-1); } } // Trace courbe "⊓" à cette échelle: private void HilbertA (int level) { if (level > 0) { HilbertC(level-1); sg.lineRel(0,-dist); HilbertA(level-1); sg.lineRel(-dist,0); HilbertA(level-1); sg.lineRel(0,dist); HilbertD(level-1); } } } class SimpleGraphics { private Graphics g = null; private int x = 0, y = 0; public SimpleGraphics(Graphics g) { this.g = g; } public void goToXY(int x, int y) { this.x = x; this.y = y; } public void lineRel(int deltaX, int deltaY) { g.drawLine ( x, y, x+deltaX, y+deltaY ); x += deltaX; y += deltaY; } }
Et voici une autre version qui met en œuvre les règles du L-système :
def f walk 10 end def p turn 90 end def m turn -90 end def l(n) return if n==0 p; r(n-1); f; m; l(n-1); f; l(n-1); m; f; r(n-1); p end def r(n) return if n==0 m; l(n-1); f; p; r(n-1); f; r(n-1); p; f; l(n-1); m end l(6)Références
- (de) D. Hilbert, « Über die stetige Abbildung einer Linie auf ein Flächenstück », dans Math. Ann., vol. 38, 1891, p. 459-460 [texte intégral]
- (en) Arthur Butz (en), « Alternative algorithm for Hilbert’s space filling curve », IEEE Trans. On Computers, 20, p.424-442, avril 1971.
Voir aussi
Articles connexes
Liens externes
- (en) Eric W. Weisstein, « Hilbert Curve », MathWorld
- (en) Plane Filling Curves sur cut-the-knot
Wikimedia Foundation. 2010.
