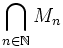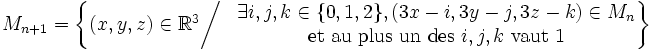- Eponge de Menger
-
Éponge de Menger
Éponge de Menger après quatre itérations
Une éponge de MengerL'éponge de Menger, parfois appelée éponge de Menger-Sierpinski, est un solide fractal. Il s'agit de l'extension dans une troisième dimension de l'ensemble de Cantor et du tapis de Sierpinski. Elle fut décrite pour la première fois par le mathématicien autrichien Karl Menger en 1926[1].
Sommaire
Définition formelle
Formellement, l'éponge de Menger M est l'ensemble:
où M0 est le cube unité et
Construction
Quatre premiers stades de la construction d'une éponge de MengerLa construction d'une éponge de Menger peut être décrite de la manière suivante :
- débuter par un cube,
- réduire le cube au tiers et en faire 20 copies,
- placer ces copies de telle façon qu'elles forment un nouveau cube de la même taille que l'original, sans les parties centrales,
- répéter le processus à partir de l'étape 2 pour chacun des 20 cubes ainsi créés.
Le solide obtenu à la limite, après un nombre infini d'itérations, est l'éponge de Menger.
À chaque itération, on multiplie le nombre de cubes par 20, ce qui fait que le solide créé à l'itération n contient 20n cubes.
Propriétés
Face d'une éponge de Menger
Eponge de Menger coupée par un plan transversalL'éponge de Menger est une fractale dont la dimension de Hausdorff vaut
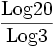, soit à peu près 2,726 833.Chaque face de l'éponge de Menger est un tapis de Sierpinski. Toute intersection de l'éponge de Menger avec une diagonale ou une médiane du cube initial est un ensemble de Cantor. L'éponge de Menger est un espace fermé ; puisqu'il est également borné, le théorème de Heine-Borel stipule qu'il est également compact. L'éponge de Menger est un ensemble non-dénombrable de mesure de Lebesgue nulle.
La dimension topologique de l'éponge de Menger est égale à 1 ; elle fut d'ailleurs construite à la base par Menger pour explorer le concept de dimension topologique. Menger démontra que l'éponge est une courbe universelle, c’est-à-dire que toute courbe unidimensionnelle (au sens où sa dimension topologique est égale à 1) est homéomorphe à un sous-ensemble de l'éponge.
De manière similaire, le triangle de Sierpinski est une courbe universelle pour toute courbe d'un espace à deux dimensions. L'éponge de Menger étend cette notion aux courbes tri-dimensionnelles. Le raisonnement peut être étendu à un nombre de dimension quelconque.
Annexes
Articles connexes
- Ensemble de Cantor
- Tapis de Sierpinski
- Triangle de Sierpinski
- Liste de fractales par dimension de Hausdorff
Liens externes
- (en) Une éponge de Menger interactive (en Java)
Bibliographie
- Karl Menger, Allgemeine Räume und Cartesische Räume I, II, communication à l'Académie des Sciences d'Amsterdam (1926), p. 29, 476-484 et 1125-1128.
- Karl Menger, Dimensionstheorie, B.G Teubner Publishers, Leipzig (1928)
Référence
- ↑ Karl Menger, Allgemeine Räume und Cartesische Räume I, II, communication à l'Académie des Sciences d'Amsterdam (1926), p. 29, 476-484 et 1125-1128.
Portail de la géométrie
Catégorie : Fractale
Wikimedia Foundation. 2010.
