Courbe De Peano

Courbe De Peano

Courbe de Peano

Quatre itérations de la courbe de Peano

Une courbe de Peano est une fonction continue sur l'intervalle [0, 1], surjective dans le carré [0, 1] x [0, 1], c'est-à-dire que la courbe passe par chaque point du carré. Elle est une fractale : bien que formée d'une simple ligne, elle est de dimension 2. Une courbe de Peano est généralement décrite comme limite d'une suite de courbes. Cette courbe est nommée en l'honneur de Giuseppe Peano qui fut le premier à la décrire.

Les travaux de Hilbert ont ainsi donné naissance à une famille de courbes nommées courbes de Peano-Hilbert.

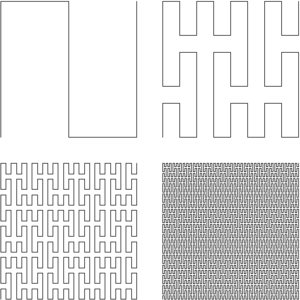
Hilbert curve.png Six itérations de la courbe de Hilbert.

Remarque. La courbe de Peano est 1/2-höldérienne. Néanmoins, il est impossible d'obtenir une application a-höldérienne surjective de [0,1] sur [0,1]^2 pour a>1/2. La preuve est mentionnée dans l'article Condition de Hölder.

Citations

« J'ai la plus grande estime pour M. Peano, qui a fait de très jolies choses (par exemple sa courbe qui remplit toute une aire), mais enfin, il n'est allé ni plus loin, ni plus haut, ni plus vite que la plupart des mathématiciens aptères et il aurait pu faire tout aussi bien avec ses jambes ». (Henri Poincaré, Science et méthode).

Voir aussi

Liens externes

  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Courbe de Peano ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Courbe De Peano de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Courbe de Péano — Courbe de Peano Quatre itérations de la courbe de Peano Une courbe de Peano est une fonction continue sur l intervalle [0, 1], surjective dans le carré [0, 1] x [0, 1], c est à dire que la courbe passe par chaque point du carré. Elle est une… …   Wikipédia en Français

  • Courbe de peano — Quatre itérations de la courbe de Peano Une courbe de Peano est une fonction continue sur l intervalle [0, 1], surjective dans le carré [0, 1] x [0, 1], c est à dire que la courbe passe par chaque point du carré. Elle est une fractale : bien …   Wikipédia en Français

  • courbe de Peano — ● courbe de Peano Arc paramétré (I, f), où f est une application continue de I = [0, 1] dans E2, plan affine, dont le support passe par tous les points d un carré. (C est un des premiers exemples de fractale.) …   Encyclopédie Universelle

  • Courbe de Peano — Giuseppe Peano Une courbe de Peano est une courbe plane paramétrée par une fonction continue sur l intervalle unité [0, 1], surjective dans le carré [0, 1]×[0, 1], c est à dire que la courbe passe par chaque point du carré : elle… …   Wikipédia en Français

  • PEANO (G.) — Le mathématicien italien Peano s’est principalement intéressé aux fondements des mathématiques, ainsi qu’à la théorie des langages. Grâce à lui, on comprendra mieux aujourd’hui la fécondité des méthodes formelles et axiomatiques. L’actualité de… …   Encyclopédie Universelle

  • Courbe Plane — En géométrie, une courbe plane est une courbe qui est entièrement contenue dans un (unique) plan, et qui est identifiable à une fonction continue : où I est un intervalle de l ensemble des nombres réels. L image d une courbe est aussi… …   Wikipédia en Français

  • Courbe de Gosper — à la 4ème itération La Courbe de Gosper, baptisée d après son découvreur Bill Gosper, est une courbe de Peano remplissant le plan. Il s agit d une courbe fractale, voisine, dans sa construction, à la courbe du dragon ou la courbe de Hilbert …   Wikipédia en Français

  • Courbe rectifiable — Longueur d un arc Camille Jordan est l auteur de la définition la plus courante de la longueur d un arc. En géométrie, la question de la longueur d un arc est intuitivement simple à concevoir. L idée d arc correspond à celle d une ligne, ou d une …   Wikipédia en Français

  • Courbe — En géométrie, le mot courbe, ou ligne courbe désigne certains sous ensembles du plan, de l espace usuels. Par exemple, les droites, les segments, les lignes polygonales et les cercles sont des courbes. La notion générale de courbe se décline en… …   Wikipédia en Français

  • Peano — Giuseppe Peano Giuseppe Peano Giuseppe Peano (Spinetta di Cuneo (Coni), 27 août 1858 Turin, 20 avril 1932) est un mathématicien italien de la fin du XIXe et du début du …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”