- Dimension Topologique
-
Dimension topologique
On donne ici la définition classique, par récurrence, de la dimension topologique d'un espace métrisable à base dénombrable E. Si E est vide, sa dimension vaut -1 par convention ; sinon on pose :
- 0) L'espace E est de dimension 0 si sa topologie admet une base de parties à la fois ouvertes et fermées (clopen en anglais), soit encore une base de parties à frontière vide (ou de dimension -1). On dit aussi que E est totalement discontinu.
- 1) L'espace E est au plus de dimension 1 si sa topologie admet une base d'ouverts à frontière de dimension au plus 0.
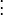
- n) L'espace E est de dimension au plus n si sa topologie admet une base d'ouverts à frontière de dimension au plus n-1.
Enfin l'espace E non vide est dit de dimension n s'il est de dimension au plus n mais n'est pas de dimension au plus n-1, et de dimension infinie s'il n'existe pas de n tel qu'il soit de dimension au plus n.
L'ensemble de Cantor (ou l'espace de Cantor qui lui est homéomorphe) est un espace compact de dimension 0 ; l'espace NN est le parangon des espaces polonais de dimension 0. Un arc de Jordan rectifiable dans Rn est de dimension 1, une portion de surface régulière est de dimension 2, etc. Comme il se doit la dimension de tout ouvert non vide de Rn est n.
La dimension introduite ci-dessus, à valeur entière, est une notion topologique alors que la notion de dimension de Hausdorff, à valeur réelle, est métrique, et dépend fortement de la distance utilisée. Il existe cependant une belle relation entre les deux quand E est un espace compact métrisable :
- La dimension topologique de E est le minimum des dimensions de Hausdorff de E pour toutes les distances sur E compatibles avec sa topologie.
- Portail des mathématiques
Catégorie : Topologie
Wikimedia Foundation. 2010.
