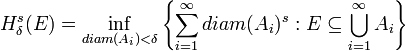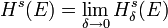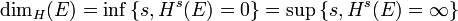Dimension de hausdorff

Dimension de Hausdorff

En topologie, la dimension de Hausdorff d'un espace métrique (X,d) est un nombre réel positif ou nul, éventuellement l'infini. Si deux métriques sont Lipschitz-équivalentes, alors elles ont la même dimension de Hausdorff. Introduite en 1918 par le mathématicien Felix Hausdorff, elle a été développée par Abram Samoilovitch Besicovitch. Elle est parfois appelée dimension de Hausdorff-Besicovitch.

Un espace vectoriel réel de dimension finie E peut être muni d'une norme et toutes les normes sont équivalentes. La dimension de Hausdorff de E fait sens et vaut la dimension de E - telle qu'elle est définie en algèbre linéaire. Cependant, en général, la dimension de Hausdorff n'est pas entière. Par exemple, la dimension de Hausdorff d'une courbe peut être strictement supérieure à 1. Il est possible de rencontrer des espaces métriques compacts de dimension 0 qui ne soient pas finis.

Sommaire

1 Introduction informelle
2 Définition
3 Calcul pratique dans un cas particulier classique
4 Propriétés
5 Exemples
6 Liens internes

Introduction informelle

Intuitivement, la dimension d'un ensemble à l'instar d'une partie d'un espace euclidien est le nombre de paramètres indépendants pour décrire un point dans cet ensemble. Ainsi a-t-on besoin d'un seul paramètre pour décrire un point sur une règle, de deux paramètres pour décrire la position d'un clou sur un mur, de trois paramètres pour décrire la position d'une balle de tennis dans l'espace, et plus généralement de n paramètres pour décrire un point dans $\R^n$ .

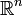Comment atteindre cette donnée en utilisant uniquement la structure métrique ? Si on dispose de d paramètres pour repérer un point, pour l'approximer à $\varepsilon$ près, on devrait disposer d'un 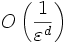$O\left(\frac{1}{\varepsilon^d}\right)$ points. Soit X un espace métrique compact. Posons N(r) le nombre minimal de boules ouvertes de rayon r nécessaires pour recouvrir X. Lorsque $N (r)$ croît comme 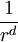$\frac{1}{r^d}$ , l'espace X est dit de dimension d.

Une introduction à cette notion sur le sujet suivant : http://www.corriges-mathprepa.fr/corriges-1980/pdf/m80tm2ea.pdf

Définition

La dimension de Haussdorff offre un moyen usuel de calcul de la dimension d'un espace métrique. Sa définition requiert l'étude des mesures de Hausdorff H^s

$H^s_{\delta}(E)=\inf_{diam(A_i) < \delta}{\left\{\sum_{i=1}^{\infty}diam(A_i)^s : E \subseteq \bigcup_{i=1}^\infty A_i\right\}}$

$H^s(E)=\lim_{\delta\rightarrow 0}H^s_{\delta}(E)$

$\dim_H(E)=\inf\left\{s,H^s(E)=0\right\}=\sup\left\{s,H^s(E)=\infty\right\}$

Calcul pratique dans un cas particulier classique

Si E est une partie d'un ℝ-espace vectoriel qui vérifie la propriété suivante :

« Il existe n similitudes f₁, f₂, …, $f n$ de rapports r₁, r₂, …, $r n$ telles que f₁(E), f₂(E), …, $f n (E)$ soient disjoints deux à deux et que leur union soit isométrique avec E. »,

alors on a la relation :

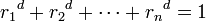${r_1}^d + {r_2}^d + \cdots + {r_n}^d = 1$ , où d est la dimension de E.

Cela découle de la propriété suivante des mesures de Hausdorff :

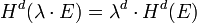« Pour tout λ positif, $H^d(\lambda \cdot E) = \lambda^d \cdot H^d(E)$ . »

et de l'invariance par isométrie. Cela offre un moyen simple de calculer les dimensions de fractales classiques, telles le flocon de Koch, le tapis de Sierpinski, etc.

Exemple.

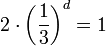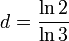L'ensemble de Cantor est constituée de deux ensembles de Cantor trois fois plus petits ; les deux similitudes sont donc ici des homothéties de rapports 1/3, composées avec des translations. Donc $2 \cdot \left(\frac{1}{3}\right)^d = 1$ , ce qui donne : $d = \frac{\ln{2}}{\ln{3}} ~$ .

Propriétés

La dimension de Hausdorff d'un produit d'espaces métriques est supérieure à la somme des dimensions de Hausdorff. Explicitement, pour tous espaces métriques X et Y, on a :

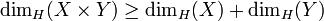$\dim_H(X\times Y)\geq \dim_H(X)+\dim_H(Y)$ .

Une fonction lipschitzienne diminue la dimension de Hausdorff. Plus généralement, si 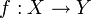$f:X\rightarrow Y$ est une fonction a-höldérienne entre espaces métriques (avec 0<a<1), alors on a :

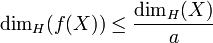$\dim_H(f(X))\leq \frac{\dim_H(X)}{a}$ .

Pour $a s > dim H X$ , il existe un recouvrement ouvert dénombrable $A i$ de X de diamètre inférieur à $δ > 0$ tel que 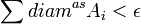$\sum diam^{as}A_i<\epsilon$ . Comme f est a-höldérienne, il existe une constante C telle que f envoie toute partie A de diamètre d sur une partie de diamètre $< C d a$ . Soit $B i$ un voisinage ouvert sufficamment petit de $f (A i)$ . On peut supposer que le diamètre de $B i$ soit inférieure à $2 C d i a m a A i$ (et donc en particulier $δ' = C δ a$ ). 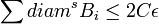Par construction, $\sum diam^s B_i\leq 2C\epsilon$ .

Il s'en suit $H s (f (X)) = 0$ pour $a s > dim H X$ .

Exemples

Triangle de Sierpinski, de dimension de Hausdorff $\frac{\ln{3}}{\ln{2}} ~$ ..

Le cercle est de dimension de Hausdorff 1.
Le graphe d'une fonction d'une variable réelle lipschitzienne est de dimension de Hausdorff 1. Si la fonction est a-höldérienne, alors la dimension de Hausdorff de son graphe est comprise entre 1 et 2-a.
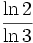La dimension de Hausdorff de l'ensemble triadique de Cantor est $\frac{\ln{2}}{\ln{3}} ~$ .
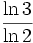La dimension de Hausdorff du triangle de Sierpinski est $\frac{\ln{3}}{\ln{2}} ~$ .
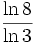La dimension de Hausdorff du tapis de Sierpinski est $\frac{\ln{8}}{\ln{3}} ~$ .
La trajectoire du mouvement brownien en dimension 2 est presque sûrement de dimension 2.

Liens internes

Liste de fractales par dimension de Hausdorff

Portail de la géométrie

Ce document provient de « Dimension de Hausdorff ».

Catégories : Fractale | Théorie de la mesure

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Dimension de hausdorff de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Dimension De Hausdorff — En topologie, la dimension de Hausdorff d un espace métrique (X,d) est un nombre réel positif ou nul, éventuellement l infini. Si deux métriques sont Lipschitz équivalentes, alors elles ont la même dimension de Hausdorff. Introduite en 1918 par… … Wikipédia en Français
Dimension de Hausdorff — En mathématiques, et plus précisément en topologie, la dimension de Hausdorff d un espace métrique (X,d) est un nombre réel positif ou nul, éventuellement l infini. Introduite en 1918 par le mathématicien Felix Hausdorff, elle a été développée… … Wikipédia en Français
Dimensión de Hausdorff-Besicovitch — Saltar a navegación, búsqueda La dimensión de Hausdorff o dimensión de Hausdorff Besicovitch es una generalización métrica del concepto de dimensión de un espacio topológico, que permite definir la dimensión de una dimensión fraccionaria (no… … Wikipedia Español
Liste De Fractales Par Dimension De Hausdorff — Cet article est une liste de fractales, ordonnées par dimension de Hausdorff croissante. En mathématiques, une fractale est un ensemble dont la dimension de Hausdorff (notée δ) est strictement supérieure à la dimension topologique[1]. Sommaire 1… … Wikipédia en Français
Liste de fractales par dimension de Hausdorff — Cet article est une liste de fractales, ordonnées par dimension de Hausdorff croissante. En mathématiques, une fractale est un ensemble dont la dimension de Hausdorff (notée δ) est strictement supérieure à la dimension topologique[1]. Sommaire 1… … Wikipédia en Français
Liste de fractales par dimension de hausdorff — Cet article est une liste de fractales, ordonnées par dimension de Hausdorff croissante. En mathématiques, une fractale est un ensemble dont la dimension de Hausdorff (notée δ) est strictement supérieure à la dimension topologique[1]. Sommaire 1… … Wikipédia en Français
Dimension box-counting — Dimension de Minkowski–Bouligand En géométrie fractale, la dimension de Minkowski–Bouligand, également appelée dimension de Minkowski ou dimension box counting, est une manière de déterminer la dimension fractale d un ensemble S dans un Espace… … Wikipédia en Français
Dimension de Minkowski — Dimension de Minkowski–Bouligand En géométrie fractale, la dimension de Minkowski–Bouligand, également appelée dimension de Minkowski ou dimension box counting, est une manière de déterminer la dimension fractale d un ensemble S dans un Espace… … Wikipédia en Français
Dimension de Hamel — Dimension Voir « dimension » sur le Wiktionnaire … Wikipédia en Français
Dimension spatiale — Dimension Voir « dimension » sur le Wiktionnaire … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Dimension de hausdorff